Kluczową cechą rozbudowanej formy, która odróżnia ją od drzew gry, jest to, że może uchwycić częściową obserwowalność. Teoretycy gier używają terminu niedoskonałe informacje do opisania sytuacji, w których gracze nie są pewni rzeczywistego stanu gry. Niestety, indukcja wsteczna nie działa w grach z niedoskonałą informacją i ogólnie są one znacznie bardziej złożone do rozwiązania niż gry z doskonałą informacją. W podrozdziale 6.6 widzieliśmy, że gracz w częściowo obserwowalnej grze, takiej jak Kriegspiel, może stworzyć drzewo gry w przestrzeni stanów przekonań. Na tym drzewku widzieliśmy, że w niektórych przypadkach gracz może znaleźć sekwencję ruchów (strategię), która prowadzi do wymuszonego mata, niezależnie od tego, w jakim stanie zaczęliśmy i bez względu na to, jakiej strategii używa przeciwnik. Jednak techniki opisane w rozdziale 6 nie mogą powiedzieć graczowi, co ma zrobić, gdy nie ma zagwarantowanego mata. Jeśli najlepsza strategia gracza zależy od strategii przeciwnika i odwrotnie, to minimax (lub alfa-beta) sam w sobie nie może znaleźć rozwiązania. Rozbudowana forma pozwala nam znaleźć rozwiązania, ponieważ reprezentuje stany przekonań (teoretycy gier nazywają je zbiorami informacji) wszystkich graczy jednocześnie. Z tej reprezentacji możemy znaleźć rozwiązania równowagi, tak jak to zrobiliśmy w grach o postaci normalnej. Jako prosty przykład gry sekwencyjnej, umieść dwóch agentów w świecie 4×3 z rysunku wcześniejszym i pozwól im poruszać się jednocześnie, aż jeden agent dotrze do pola wyjściowego i otrzyma zapłatę za to pole. Jeśli określimy, że żaden ruch nie występuje, gdy dwaj agenci próbują jednocześnie wjechać na ten sam plac (powszechny problem na wielu skrzyżowaniach), wtedy pewne czyste strategie mogą utknąć na zawsze. Dlatego agenci potrzebują mieszanej strategii, aby dobrze radzić sobie w tej grze: losowo wybieraj między pójściem do przodu a pozostaniem w miejscu. Właśnie to robi się, aby rozwiązać kolizje pakietów w sieciach Ethernet. Następnie rozważymy bardzo prosty wariant pokera. Talia ma tylko cztery karty, dwa asy i dwa króle. Każdy gracz otrzymuje jedną kartę. Pierwszy gracz ma wtedy możliwość podniesienia stawki gry z 1 punktu do 2 lub przeczekania. Jeśli gracz 1 sprawdzi, gra się kończy. Jeśli gracz 1 przebije, wówczas gracz 2 może sprawdzić, akceptując, że gra jest warta 2 punkty, lub spasować, tracąc 1 punkt. Jeśli gra nie kończy się spasowaniem, wypłata zależy od kart: wynosi zero dla obu graczy, jeśli mają tę samą kartę; w przeciwnym razie gracz z królem płaci stawki graczowi z asem. Drzewo postaci ekstensywnej dla tej gry pokazano na rysunku. Gracz 0 to szansa; Gracze 1 i 2 są oznaczeni trójkątami. Każda akcja jest przedstawiona jako strzałka z etykietą, odpowiadającą podbiciu, zaczekaniu, sprawdzeniu lub spasowaniu, lub, w przypadku przypadku, czterem możliwym rozdaniom („AK” oznacza, że gracz 1 otrzymuje asa, a gracz 2 króla). Stany końcowe to prostokąty oznaczone według ich wypłat dla gracza 1 i gracza 2. Zestawy informacji są pokazane jako oznaczone kreskowanymi polami; na przykład I1;1 to zestaw informacji, w którym jest tura gracza 1, a on wie, że ma asa (ale nie wie, co ma gracz 2). W zestawie informacji I2;1 jest tura gracza nr 2, który wie, że ma asa i że gracz nr 1 przebił, ale nie wie, jaką kartę ma gracz nr 1. (Ze względu na ograniczenia dwuwymiarowego papieru, ten zestaw informacji jest pokazany jako dwa pola, a nie jedno). Jednym ze sposobów rozwiązania rozbudowanej gry jest przekształcenie jej w grę w normalnej formie. Przypomnijmy, że forma normalna to macierz, której każdy wiersz jest oznaczony czystą strategią dla gracza 1, a każda kolumna czystą strategią dla gracza 2. W rozbudowanej grze czysta strategia dla gracza i odpowiada akcji dla każdego zestaw informacji dotyczących tego gracza. Tak więc na rysunku jedną czystą strategią dla gracza 1 jest „podbicie, gdy mam I1;1 (to znaczy, kiedy mam asa) i czekanie, gdy mam I1;2 (kiedy mam króla)”. W poniższej macierzy wypłat strategia ta nazywa się rk. Podobnie strategia cf dla gracza 2 oznacza „sprawdzenie, gdy mam asa i spasowanie, gdy mam króla”. Ponieważ jest to gra o sumie zerowej, poniższa macierz daje tylko wypłatę dla gracza 1; gracz 2 zawsze ma odwrotną wypłatę:
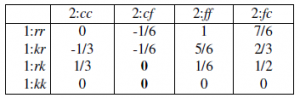
Ta gra jest tak prosta, że ma dwie czysto-strategiczne równowagi, zaznaczone pogrubioną czcionką: cf dla gracza 2 i rk lub kk dla gracza 1. Ogólnie jednak możemy rozwiązywać rozbudowane gry, konwertując do postaci normalnej, a następnie znajdując rozwiązanie (zazwyczaj strategia mieszana) przy użyciu standardowych metod programowania liniowego. To działa w teorii. Ale jeśli gracz ma zestawy informacji i akcje na zestaw, to będzie miał czyste strategie. Innymi słowy, rozmiar macierzy o postaci normalnej jest wykładniczy w liczbie zbiorów informacji, więc w praktyce podejście działa tylko w przypadku małych drzew gry – około tuzina stanów. Gra taka jak poker Texas hold’em dla dwóch graczy ma około 1018 stanów, co sprawia, że takie podejście jest całkowicie niewykonalne. Jakie są alternatywy? W rozdziale 6 zobaczyliśmy, jak wyszukiwanie alfa-beta może obsługiwać gry z doskonałą informacją z ogromnymi drzewami łownymi poprzez przyrostowe generowanie drzewa, przycinanie niektórych gałęzi i heurystyczną ocenę węzłów nieterminalnych. Ale to podejście nie sprawdza się dobrze w grach z niedoskonałymi informacjami z dwóch powodów: po pierwsze, trudniej jest przycinać, ponieważ musimy rozważyć strategie mieszane, które łączą wiele gałęzi, a nie czystą strategię, która zawsze wybiera najlepszą gałąź. Po drugie, trudniej jest ocenić heurystycznie węzeł nieterminal, ponieważ mamy do czynienia ze zbiorami informacji, a nie z poszczególnymi stanami. Koller przyszedł na ratunek z alternatywną reprezentacją rozległych gier, zwaną formą sekwencji, która jest tylko liniowa w rozmiarze drzewa, a nie wykładnicza. Zamiast przedstawiać strategie, reprezentuje ścieżki przez drzewo; liczba ścieżek jest równa liczbie węzłów końcowych. W tej reprezentacji można ponownie zastosować standardowe metody programowania liniowego. Powstały system może rozwiązać warianty pokera z 25 000 stanami w minutę lub dwie. Jest to wykładnicze przyspieszenie w stosunku do podejścia z normalną formą, ale nadal jest dalekie od obsługi, powiedzmy, dwuosobowego Texas Hold’em z 1018 stanami. Jeśli nie możemy obsłużyć 1018 stanów, być może możemy uprościć problem, zmieniając grę na prostszą formę. Na przykład, jeśli mam asa i rozważam możliwość, że następna karta da mi parę asów, nie obchodzi mnie kolor następnej karty; zgodnie z zasadami pokera każdy kolor sprawdzi się równie dobrze. Sugeruje to tworzenie abstrakcji gry, w której kolory są ignorowane. Powstałe drzewo gry będzie mniejsze 4!=24. Załóżmy, że potrafię rozwiązać tę mniejszą grę; jak rozwiązanie tej gry będzie miało związek z oryginalną grą? Jeśli żaden gracz nie myśli o kolorze (jedynym rozdaniu, w którym liczą się kolory), to rozwiązanie abstrakcji będzie również rozwiązaniem dla oryginalnej gry. Jeśli jednak jakiś gracz rozważa kolor, to abstrakcja będzie tylko przybliżonym rozwiązaniem (ale możliwe jest obliczenie granic błędu). Istnieje wiele możliwości abstrakcji. Na przykład w momencie gry, w której każdy gracz ma dwie karty, jeśli mam parę dam, to ręce innych graczy mogą zostać podzielone na trzy klasy: lepiej (tylko para króli lub para asów) , to samo (para królowych) lub gorzej (wszystko inne). Jednak ta abstrakcja może być zbyt prostacka. Lepsza abstrakcja podzieliłaby gorzej na, powiedzmy, średnią parę (od dziewiątek do waletów), niską parę i brak pary. Te przykłady są abstrakcjami stanów; możliwe jest również abstrahowanie działań. Na przykład, zamiast mieć akcję zakładu dla każdej liczby całkowitej od 1 do 1000, możemy ograniczyć zakłady do 100, 101, 102 i 103. Albo możemy całkowicie wyciąć jedną z rund licytacji. Możemy również abstrahować od węzłów przypadkowych, biorąc pod uwagę tylko podzbiór możliwych transakcji. Jest to równoważne technice rollout używanej w programach Go. Łącząc wszystkie te abstrakcje, możemy zredukować 1018 stanów pokera do 107 stanów, co jest wielkością, którą można rozwiązać za pomocą obecnych technik. W rozdziale 6 widzieliśmy, jak programy pokerowe, takie jak Libratus i DeepStack, były w stanie pokonać zwycięskich ludzkich graczy w heads-upie (dwóch graczy) w pokera Texas hold’em. Niedawno program Pluribus był w stanie pokonać ludzkich mistrzów w sześcioosobowym pokerze w dwóch formatach: pięć kopii programu przy stole z jednym człowiekiem i jedna kopia programu z pięcioma ludźmi. Mamy tu do czynienia z ogromnym skokiem złożoności. Z jednym przeciwnikiem jest możliwości ukrytych kart przeciwnika. Ale z pięcioma przeciwnikami jest 50wybrów10 ≈ 10 miliardów możliwości. Pluribus opracowuje podstawową strategię całkowicie na podstawie własnej gry, a następnie modyfikuje strategię podczas rzeczywistej gry, aby reagować na konkretną sytuację. Pluribus wykorzystuje kombinację technik, w tym wyszukiwanie drzewa Monte Carlo, wyszukiwanie z ograniczoną głębokością i abstrakcję. Forma rozbudowana jest wszechstronną reprezentacją: może obsługiwać częściowo obserwowalne, wieloagentowe, stochastyczne, sekwencyjne środowiska czasu rzeczywistego — większość trudnych przypadków z listy właściwości środowiska na stronie 61. Istnieją jednak dwa ograniczenia formy rozszerzonej w szczególności i ogólnie teorii gier. Po pierwsze, nie radzi sobie dobrze ze stanami i działaniami ciągłymi (chociaż istnieją pewne rozszerzenia przypadku ciągłego; na przykład teoria konkurencji Cournota wykorzystuje teorię gier do rozwiązywania problemów, w których dwie firmy wybierają ceny za swoje produkty z przestrzeni ciągłej ). Po drugie, teoria gier zakłada, że gra jest znana. Niektóre części gry mogą być określone jako nieobserwowalne dla niektórych graczy, ale trzeba wiedzieć, które części są nieobserwowalne. W przypadkach, w których gracze poznają z czasem nieznaną strukturę gry, model zaczyna się załamywać. Zbadajmy każde źródło niepewności i czy każde z nich może być reprezentowane w teorii gier.
Akcje: Nie ma łatwego sposobu na przedstawienie gry, w której gracze muszą odkryć, jakie akcje są dostępne. Rozważ grę między twórcami wirusów komputerowych a ekspertami ds. bezpieczeństwa. Częścią problemu jest przewidywanie, jakie działania spróbują następnie podjąć twórcy wirusów.
Strategie: Teoria gier bardzo dobrze przedstawia ideę, że strategie innych graczy są początkowo nieznane – o ile zakładamy, że wszyscy agenci są racjonalni. Teoria nie mówi, co robić, gdy inni gracze nie są w pełni racjonalni. Pojęcie równowagi Bayesa-Nasha częściowo odnosi się do tego punktu: jest to równowaga w odniesieniu do wcześniejszego rozkładu prawdopodobieństwa gracza względem strategii innych graczy – innymi słowy, wyraża przekonania gracza na temat prawdopodobnych strategii innych graczy.
Szansa: Jeśli gra zależy od rzutu kostką, dość łatwo jest wymodelować węzeł losowy z równomiernym rozkładem wyników. Ale co, jeśli jest możliwe, że kostka jest niesprawiedliwa? Możemy przedstawić to z innym węzłem losowym, wyżej w drzewie, z dwiema gałęziami dla „kostka jest sprawiedliwa” i „kostka jest niesprawiedliwa”, tak że odpowiadające węzły w każdej gałęzi znajdują się w tym samym zbiorze informacji (czyli gracze nie wiedzą, czy kość jest sprawiedliwa, czy nie). A jeśli podejrzewamy, że przeciwnik wie? Następnie dodajemy kolejny węzeł szansy, z jedną gałęzią reprezentującą przypadek, w którym przeciwnik wie, i jedną, w której przeciwnik nie.
Narzędzia: Co jeśli nie znamy narzędzi przeciwnika? Ponownie, można to zamodelować za pomocą węzła losowego, tak aby drugi agent znał swoje własne narzędzia w każdej gałęzi, ale my nie. Ale co, jeśli nie znamy własnych narzędzi? Na przykład, skąd mam wiedzieć, czy rozsądnie jest zamówić sałatkę szefa kuchni, jeśli nie wiem, jak bardzo mi się spodoba? Możemy to wymodelować za pomocą kolejnego węzła losowego określającego nieobserwowalną „wewnętrzną jakość” sałatki. Widzimy zatem, że teoria gier jest dobra w przedstawianiu większości źródeł niepewności – ale kosztem podwojenia wielkości drzewa za każdym razem, gdy dodajemy kolejny węzeł; zwyczaj, który szybko prowadzi do nieprzyjemnie dużych drzew. Z powodu tych i innych problemów teoria gier była wykorzystywana głównie do analizy środowisk, które są w równowadze, a nie do kontrolowania agentów w środowisku.