W ogólnym przypadku gra składa się z sekwencji tur, które nie muszą być takie same. Takie gry najlepiej reprezentuje drzewo gier, które teoretycy gier nazywają formą ekstensywną. Drzewo zawiera wszystkie te same informacje, które widzieliśmy w sekcji 6.1: stan początkowy S0, funkcję GRACZ(y), która mówi, który gracz ma ruch, funkcję AKCJE wyliczającą możliwe akcje, funkcję WYNIK(i;a) ), która definiuje przejście do nowego stanu, oraz funkcję częściową UTILITY(s; p), która jest zdefiniowana tylko w stanach terminalowych, aby dać wypłatę każdemu graczowi. Gry stochastyczne można uchwycić, wprowadzając wybitnego gracza, Chance, który może podejmować losowe akcje. „Strategia” Chance’a jest częścią definicji gry, określonej jako rozkład prawdopodobieństwa na działania (inni gracze mogą wybrać własną strategię). Aby reprezentować gry z niedeterministycznymi akcjami, takie jak bilard, dzielimy akcję na dwie części: sama akcja gracza ma deterministyczny skutek, a następnie Chance ma kolej, by zareagować na akcję na swój własny, kapryśny sposób. Na razie poczynimy jedno uproszczone założenie: zakładamy, że gracze mają doskonałe informacje. Z grubsza, doskonała informacja oznacza, że kiedy gra wzywa ich do podjęcia decyzji, wiedzą dokładnie, gdzie się znajdują w drzewie gry: nie mają pewności co do tego, co wydarzyło się wcześniej w grze. Tak jest oczywiście w grach takich jak szachy czy Go, ale nie w grach takich jak poker czy Kriegspiel. W dalszej części pokażemy, jak rozbudowaną formę można wykorzystać do przechwytywania niedoskonałych informacji w grach, ale na razie założymy doskonałe informacje. Strategia w rozbudowanej grze zawierającej doskonałe informacje jest funkcją dla gracza, która dla każdego z jego stanów decyzyjnych określa, które działanie w AKCJACH gracz powinien wykonać. Gdy każdy gracz wybierze strategię, wynikowy profil strategii będzie śledzić ścieżkę w drzewie gry od stanu początkowego S0 do stanu terminala, a funkcja UTILITY definiuje narzędzia, które następnie otrzyma każdy gracz. Biorąc pod uwagę tę konfigurację, możemy bezpośrednio zastosować aparat równowagi Nasha, który wprowadziliśmy powyżej, do analizy gier w formie ekstensywnej. Aby obliczyć równowagi Nasha, możemy użyć prostego uogólnienia techniki wyszukiwania minimaksowego, którą widzieliśmy w rozdziale 6. W literaturze na temat gier w formie ekstensywnej technika ta nazywana jest indukcją wsteczną – widzieliśmy już indukcję wsteczną nieformalnie używaną do analizy skończonych powtarzający się dylemat więźnia. Indukcja wsteczna wykorzystuje programowanie dynamiczne, pracując wstecz od stanów terminalowych z powrotem do stanu początkowego, progresywnie oznaczając każdy stan profilem wypłat (przypisanie wypłat graczom), który zostałby uzyskany, gdyby gra była rozgrywana optymalnie od tego momentu. Bardziej szczegółowo, dla każdego nieterminalnego stanu s, jeśli wszystkie dzieci s zostały oznaczone profilem wypłat, to oznacza to profil wypłat ze stanu potomnego, który maksymalizuje wypłatę gracza podejmującego decyzję w stanie s. (Jeśli jest remis, wybierz arbitralnie; jeśli mamy węzły losowe, oblicz oczekiwaną użyteczność.) Algorytm indukcji wstecznej gwarantuje zakończenie działania, a ponadto działa w czasie wielomianu w rozmiarze drzewa gry. Gdy algorytm wykonuje swoją pracę, śledzi strategie dla każdego gracza. Jak się okazuje, strategie te są strategiami równowagi Nasha, a profil wypłat oznaczający stan początkowy jest profilem wypłaty, który można by uzyskać grając w strategie równowagi Nasha. Tak więc strategie równowagi Nasha dla gier o postaci ekstensywnej mogą być obliczane w czasie wielomianowym przy użyciu indukcji wstecznej; a ponieważ algorytm gwarantuje oznaczenie stanu początkowego profilem wypłaty, wynika z tego, że każda gra w formie ekstensywnej ma co najmniej jedną równowagę Nasha w czystych strategiach. Są to atrakcyjne wyniki, ale jest kilka zastrzeżeń. Drzewa gry bardzo szybko stają się bardzo duże, więc wielomianowy czas działania należy rozumieć w tym kontekście. Ale co bardziej problematyczne, sama równowaga Nasha ma pewne ograniczenia, gdy jest stosowana do gier w formie ekstensywnej. Rozważ grę z rysunku
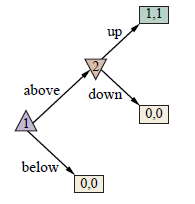
Gracz 1 ma do dyspozycji dwa ruchy: powyżej lub poniżej. Jeśli porusza się poniżej, obaj gracze otrzymują wypłatę 0 (niezależnie od ruchu wybranego przez gracza 2). Jeśli porusza się w górę, gracz 2 ma do wyboru ruch w górę lub w dół: jeśli porusza się w dół, obaj gracze otrzymują wypłatę 0, a jeśli porusza się w górę, obaj otrzymują 1. Indukcja do tyłu natychmiast nam mówi. to (powyżej; w górę) jest równowagą Nasha, co powoduje, że obaj gracze otrzymują wypłatę w wysokości 1. Jednak (poniżej; w dół) jest również równowagą Nasha, w której obaj gracze otrzymują wypłatę 0. Gracz 2 grozi graczowi 1, wskazując, że jeśli zostanie wezwany do podjęcia decyzji, wybierze przegraną, co skutkuje wypłatą 0 dla gracza 1; w tym przypadku gracz 1 nie ma lepszej alternatywy niż wybór poniżej. Problem polega na tym, że groźba gracza nr 2 (ogranie) nie jest wiarygodną groźbą, ponieważ jeśli gracz nr 2 jest rzeczywiście wezwany do dokonania wyboru, to dokona wyboru. Problem ten rozwiązuje udoskonalona równowaga Nasha, zwana idealną równowagą Nasha podgry. Aby to zdefiniować, potrzebujemy idei podgry. Każdy stan decyzyjny w podgrze drzewa gry (włącznie ze stanem początkowym) definiuje podgrę — gra na rysunku 17.4 zawiera zatem dwie podgry, jedną opartą na stanie decyzyjnym gracza 1, a drugą o stanie decyzyjnym gracza 2. Profil strategii tworzy następnie idealną równowagę Nasha dla podgry w grze G, jeśli jest to równowaga J-Nasha w każdej podgrze G. Stosując tę definicję do gry z rysunku, stwierdzamy, że (powyżej) jest idealną podgry, ale (poniżej; w dół) nie jest, ponieważ wybieranie down nie jest równowagą Nasha podgry zakorzenioną w stanie decyzji gracza 2. Chociaż potrzebowaliśmy nowej terminologii, aby zdefiniować idealną równowagę Nasha w podgry, nie potrzebujemy żadnych nowych algorytmów. Strategie obliczone przez indukcję wsteczną będą idealną równowagą Nasha dla podgry, a wynika z tego, że każda gra o doskonałej formie w formie ekstensywnej ma idealną równowagę Nasha dla podgry, którą można obliczyć w wielomianu czasu w rozmiarze drzewa gry.