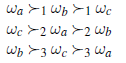Miesiąc: lipiec 2022

W AI wiedza może być reprezentowana w różny sposób, w zależności od jej struktury lub perspektywy projektanta lub rodzaju użytej struktury wewnętrznej. Skuteczna reprezentacja wiedzy (KR) powinna obejmować wiedzę niezbędną do rozwiązywania konkretnych zadań w czasie rzeczywistym. Powinna być naturalna, łatwa w utrzymaniu i zwarta. W literaturze występuje kilka rodzajów wiedzy, jak następuje:

• Wiedza deklaratywna: służy do identyfikacji czegoś i składa się głównie z faktów, obiektów i pojęć.
• Wiedza proceduralna lub wiedza imperatywna: Ta wiedza jest odpowiedzialna za wiedzę, jak coś zrobić. Składa się z zestawu zasad, strategii, planowania, agendy i wielu innych.
• Wiedza heurystyczna: Ta wiedza reprezentuje różnych ekspertów w określonej dziedzinie. Opiera się na praktycznych zasadach wynikających z przeszłych doświadczeń, ogólnej świadomości technik, z którymi praca jest owocna, ale nie reprezentujących całkowitej pewności.
• Wiedza strukturalna: Jest to rodzaj podstawowej wiedzy do rozwiązywania problemów i dotyczy relacji między obiektami. Ilustruje połączenia między różnymi rodzajami pojęć, takimi jak części, instancje i grupy czegoś.

Jednym z wpływowych protokołów negocjacyjnych jest model negocjowania ofert naprzemiennych. Dla uproszczenia ponownie przyjmiemy tylko dwóch agentów. Targowanie odbywa się w sekwencji rund. A₁ rozpoczyna, w rundzie 0, złożeniem oferty. Jeżeli A₂ przyjmie ofertę, to oferta jest realizowana. Jeśli A₂ odrzuci ofertę, negocjacje przechodzą do następnej rundy. Tym razem A₂ składa ofertę, a A₁ decyduje się ją przyjąć lub odrzucić i tak dalej. Jeśli negocjacje nigdy się nie kończą (ponieważ agenci odrzucają każdą ofertę), wówczas określamy wynik jako porozumienie w sprawie konfliktu. Wygodnym założeniem upraszczającym jest to, że obaj agenci wolą osiągnąć wynik – dowolny wynik – w skończonym czasie, niż tkwić w nieskończenie czasochłonnym układzie konfliktu. Scenariusz dzielenia tortu wykorzystamy do zilustrowania naprzemiennych ofert. Chodzi o to, że istnieje jakiś zasób („ciasto”) o wartości 1, który można podzielić na dwie części, po jednej dla każdego agenta. Zatem oferta w tym scenariuszu to para (x;1-x), gdzie x to kwota tortu, którą otrzymuje A₁, a 1-x to kwota, którą otrzymuje A₂. Przestrzeń możliwych transakcji (zestaw negocjacyjny) to zatem:

Teraz, jak agenci powinni negocjować w tym otoczeniu? Aby zrozumieć odpowiedź na to pytanie, najpierw przyjrzymy się kilku prostszym przypadkom.

Najpierw załóżmy, że pozwalamy na rozegranie tylko jednej rundy. Tak więc A₁ składa propozycję; A₂ może go zaakceptować (w takim przypadku umowa jest realizowana) lub odrzucić (w którym to przypadku umowa konfliktu jest realizowana). To jest gra ultimatum. W tym przypadku okazuje się, że A₁ – pierwszy poruszający – ma całą władzę. Załóżmy, że A₁ proponuje zdobycie całego tortu, czyli proponuje rozdanie (1;0). Jeśli A₂ odrzuci, to umowa konfliktowa zostaje wdrożona; ponieważ z definicji A₂ wolałby otrzymać 0 zamiast rozwiązania konfliktu, lepiej byłoby, gdyby A₂ to zaakceptował. Oczywiście A₁ nie może zrobić nic lepszego niż zdobycie całego tortu. Zatem te dwie strategie – A₁ proponuje uzyskanie całego tortu, a _A2 akceptuje – tworzą równowagę Nasha. Rozważmy teraz przypadek, w którym zezwalamy na dokładnie dwie rundy negocjacji. Teraz władza się zmieniła: A₂ może po prostu odrzucić pierwszą ofertę, zmieniając w ten sposób grę w grę jednorundową, w której A₂ jest pierwszym graczem iw ten sposób otrzymuje cały tort. Ogólnie rzecz biorąc, jeśli liczba rund jest stała, to ten, kto porusza się ostatni, otrzyma całe ciasto. Przejdźmy teraz do ogólnego przypadku, w którym liczba rund nie jest ograniczona. Załóżmy, że A₁ stosuje następującą strategię:

Zawsze proponuj (1;0) i zawsze odrzucaj kontrofertę.

Jaka jest najlepsza odpowiedź A₂ na to? Jeśli A₂ ciągle odrzuca propozycję, to agenci będą negocjować bez końca, co z definicji jest najgorszym wynikiem dla A₂ (jak również dla A₁). Tak więc A₂ nie może zrobić nic lepszego niż zaakceptowanie pierwszej propozycji złożonej przez A₁. Znowu jest to równowaga Nasha. Ale co, jeśli A₁ zastosuje strategię:

Zawsze proponuj (0:8;0:2) i zawsze odrzucaj każdą ofertę.

Na podstawie podobnego argumentu możemy zobaczyć, że dla tej oferty lub dla każdej możliwej transakcji (x;1-x) w zestawie negocjacyjnym, istnieje para strategii negocjacyjnych w równowadze Nasha, taka, że wynikiem będzie porozumienie w sprawie umowy w pierwszym okres czasu.

My, ludzie, jesteśmy dobrzy w percepcji, logicznym myśleniu i interpretacji wiedzy. Wiemy rzeczy – to znaczy posiadamy wiedzę – i zgodnie z naszym myśleniem działamy i wykonujemy różne rodzaje działań w scenariuszach czasu rzeczywistego. Jeśli chodzi o maszyny, wszystko, co robi człowiek, nazywa się reprezentacją wiedzy i rozumowaniem (KRR). KRR to segment AI, który zajmuje się myśleniem o agentach AI i tym, jak przyczynia się do inteligentnych zachowań agentów. Odpowiadają również za przedstawianie faktów i informacji ze świata rzeczywistego, tak aby maszyna mogła zrozumieć i rozwiązywać określone zadania, takie jak dowodzenie twierdzeń, gry, obrazowanie medyczne, przetwarzanie języka naturalnego (NLP) i wiele innych. Zasadniczo jest to metoda opisywania reprezentacji wiedzy w AI, a także umożliwienie inteligentnym maszynom uczenie się z tego i odpowiednie działanie jak człowiek. W literaturze prezentowane są różne rodzaje wiedzy, które należy reprezentować w systemach AI. Niektóre z nich to:

• Przedmiot: dotyczy faktu w prawdziwym świecie, istoty, rzeczy: gitary, klasy, człowieka, krzesła itp. Na przykład gitara ma struny, a klasa ma tablicę i krzesła .
• Wydarzenie: Akcja, która ma miejsce w prawdziwym świecie.
• Meta-wiedza: porcja danych reprezentująca wiedzę w świecie rzeczywistym.
• Fakty: Oznacza stwierdzenie, które jest prawdziwe w świecie rzeczywistym.
• Baza wiedzy (KB): Znana również jako główny składnik agentów opartych na wiedzy. Jest to baza danych służąca do udostępniania i zarządzania wiedzą.

Różne bazy danych są skonstruowane w taki sposób, że nie tylko przechowują dane, ale także znajdują rozwiązania dodatkowych problemów, korzystając z zapisanych w nich danych z przeszłości. KB odgrywa bardzo ważną rolę w AI, co można wyrazić poprzez rozważenie metodologii stosowanej przez systemy AI . Procedura wygląda następująco:

• Blok percepcji: zawiera zestaw zmysłów dla maszyn lub jest podstawowym komponentem, za pomocą którego interakcja między systemem a jego środowisko ma miejsce. Mogą to być dane, tekst, wideo, dźwięk, temperatura lub wiele innych rzeczy.
• Blok uczenia się: W tym bloku szkolone są modele, które są wymagane do pracy maszyny. W tym bloku kodowane są algorytmy uczenia, takie jak uczenie maszynowe (ML) i głębokie uczenie (DL). Blok ten jest bezpośrednio połączony z blokiem percepcji w celu uzyskania informacji wymaganych do uczenia modeli.
• Rozumowanie – Blok reprezentacji wiedzy: Jest to najbardziej krytyczny blok, który skutecznie pobiera dane wejściowe z bloku percepcji i wydobywa z niego ważne informacje. Ten blok zapewnia, że ​​wiedza jest łatwo dostępna i może zostać dostarczona modelowi lub agentowi uczenia się, jeśli jest to wymagane.
• Blok planowania i wykonania: Pobiera dane wejściowe z powyższego rozumowania – blok wiedzy i zapewnia funkcjonalną mapę drogową do maszyny. Określa również działania, które należy podjąć, a także oczekiwany wynik.

Targowanie się lub negocjacje to kolejny mechanizm często używany w życiu codziennym. Jest badany w teorii gier od lat pięćdziesiątych, a ostatnio stał się zadaniem dla zautomatyzowanych agentów. Negocjacje stosuje się, gdy agenci muszą dojść do porozumienia w sprawie będącej przedmiotem wspólnego zainteresowania. Agenci składają sobie nawzajem oferty (zwane również propozycjami lub umowami) zgodnie z określonymi protokołami i akceptują lub odrzucają każdą ofertę.

Sztuczna inteligencja to jeden z ważnych obszarów informatyki/nauki o danych, umożliwiający maszynie wykonywanie zadań w sposób podobny do człowieka, który je wykonuje. Jego głównym celem jest umożliwienie maszynom przetwarzania informacji i podejmowania decyzji w oparciu o te informacje, w taki sam sposób, w jaki robią to ludzie. Jednak nauka i przemysł sztucznej inteligencji są dalekie od pełnego zbadania i rozwoju. W szczególności AI/ML/DL mają znaczny potencjał, aby życie ludzi było bezpieczniejsze i łatwiejsze. Sugeruje się, że w przyszłości sztuczna inteligencja pomoże ludziom w wielu innych zadaniach, które są obecnie w powijakach, takich jak na przykład podróże kosmiczne. Roboty w dzisiejszych czasach wykonują wiele zadań, które w przeszłości wykonywali ludzie. Ale roboty nie mogą funkcjonować bez kontroli człowieka, programowania, debugowania i analizy. Roboty oparte na sztucznej inteligencji sprawiłyby, że ludzkie życie stałoby się wygodniejsze, a wkrótce staną się istotną częścią naszego codziennego życia w taki sam sposób, w jaki komputery były od lat 80. XX wieku. Mimo to, chociaż sztuczna inteligencja staje się coraz bardziej rozpowszechniona w wielu aplikacjach, nie zastąpi ona całkowicie ludzkich operatorów. W dłuższej perspektywie oczekuje się, że sztuczna inteligencja zwiększy ludzkie zdolności i stanie się dominującą technologią przyszłości.

Oprócz twierdzenia Arrowa, kolejnym ważnym negatywnym wynikiem w obszarze teorii wyboru społecznego jest twierdzenie Gibbarda-Satterthwaite’a. Wynik ten odnosi się do okoliczności, w których wyborca ​​może czerpać korzyści z błędnego przedstawiania swoich preferencji. Przypomnijmy, że funkcja wyboru społecznego przyjmuje jako dane wejściowe kolejność preferencji dla każdego wyborcy, a jako wynik daje zestaw zwycięskich kandydatów. Każdy wyborca ​​ma oczywiście swoje własne prawdziwe preferencje, ale w definicji funkcji wyboru społecznego nie ma nic, co wymagałoby od wyborców, aby zgłaszali swoje preferencje zgodnie z prawdą; mogą zadeklarować dowolne preferencje. W niektórych przypadkach może mieć sens, by wyborca ​​błędnie przedstawiał swoje preferencje. Na przykład w głosowaniu wieloosobowym wyborcy, którzy uważają, że preferowany przez nich kandydat nie ma szans na wygranie głosowania na swój drugi wybór. Oznacza to, że głosowanie pluralistyczne jest grą, w której wyborcy muszą myśleć strategicznie (o innych wyborcach), aby zmaksymalizować swoją oczekiwaną użyteczność. Rodzi to interesujące pytanie: czy możemy zaprojektować mechanizm głosowania, który jest odporny na taką manipulację – mechanizm, który ujawnia prawdę? Twierdzenie Gibbarda-Satterthwaite’a mówi nam, że nie możemy: Każda funkcja wyboru społecznego, która spełnia warunek Pareto dla Ja omain z więcej niż dwoma wynikami, jest albo manipulowalna, albo dyktaturą. Oznacza to, że w przypadku każdej „rozsądnej” procedury wyboru społecznego zaistnieją pewne okoliczności, w których wyborca ​​może zasadniczo skorzystać z błędnego przedstawiania swoich preferencji. Nie mówi nam jednak, jak można dokonać takiej manipulacji; i nie mówi nam, że taka manipulacja jest prawdopodobna w praktyce

Sztuczna inteligencja ma szerokie zastosowania. Coraz więcej branż, takich jak edukacja, opieka zdrowotna, podróże, rozrywka, finanse i marketing, w dużym stopniu polega na jego zdolności do rozwiązywania złożonych problemów i sprawnego wykonywania złożonych funkcji. Jest również używany w planowaniu wojskowym, inteligentnym ruchu pojazdów, monitorowaniu transakcji kartami kredytowymi, robotach, wykrywaniu oszustw związanych z kartami kredytowymi, samochodach itp. Sztuczna inteligencja stara się, aby codzienne życie użytkowników było znacznie łatwiejsze i wygodniejsze. Poniżej wymieniono niektóre obszary, w których można zastosować sztuczną inteligencję:

1. AI jako usługa (AIaaS): wdrożenie platformy AI może być:

drogie, ponieważ wiąże się z kosztami sprzętu, oprogramowania i personelu. Dlatego wiele firm włącza sztuczną inteligencję do swoich produktów, aby zapewnić dostęp do platform AIaaS (Tucci, 2020). AIaaS pozwala eksperymentować z różnymi platformami AI dla firm i aplikacji przed dużymi inwestycjami w platformę AI. Popularne oferty chmurowe oparte na sztucznej inteligencji obejmują IBM Watson Assistant, Amazon AI, Google AI, Microsoft Cognitive Services itp.

2. Samochody: Wiele branż motoryzacyjnych zapewnia swoim użytkownikom wirtualnych asystentów opartych na sztucznej inteligencji, takich jak TeslaBot firmy Tesla, aby poprawić wydajność jazdy. Sztuczna inteligencja jest obecnie wykorzystywana do opracowywania samochodów bez kierowcy. Te samochody, za pomocą systemów AI, będą w stanie hamować, zmieniać pasy, nawigować itp. Takie samochody będą badać wzorce innych otaczających samochodów poruszających się po drodze i wykonywać ruchy niezbędne do bezpiecznej jazdy autonomicznie. Pojazdy autonomiczne wykorzystują widzenie komputerowe, rozpoznawanie obrazu i DL, aby nawigować pojazdem na danym pasie, a jednocześnie omijać przeszkody, takie jak dzielniki, piesi, słupy świetlne, zwierzęta itp.
3. Rolnictwo: sztuczna inteligencja pojawia się w rolnictwie, które wymaga różnych zasobów do uzyskania najlepszych plonów. Robotyka rolnicza jest stosowana w rolnictwie do monitorowania upraw i analiz predykcyjnych, aby pomóc rolnikom. Techniki sztucznej inteligencji w rolnictwie pomagają zwiększyć produktywność i plony.
4. Bankowość: Banki używają chatbotów do świadczenia usług i oferowania swoim klientom oraz do obsługi transakcji bez udziału człowieka. Wirtualni asystenci AI usprawniają usługi i obniżają koszty placówek. Organizacje finansowe wykorzystują sztuczną inteligencję, aby usprawnić podejmowanie decyzji dotyczących pożyczek, śledzić zatwierdzone pożyczki, ustalać limity kredytowe, a także podkreślać możliwości inwestycyjne swoim klientom (Tucci, 2020).
5. Biznes: Biznes może wykorzystywać rozwiązania oparte na sztucznej inteligencji do oceny słabych i mocnych stron, aby między innymi poprawić zarządzanie finansami i relacjami z klientami (CRM). AI może pomóc w automatyzacji prac, oszczędzając znaczną ilość czasu i siły roboczej. Algorytmy ML, które mogą lepiej służyć klientom, są zintegrowane z platformami analitycznymi i CRM. Jednostki produkcyjne mogą poprawić ilość i jakość swojej produkcji, wykorzystując sztuczną inteligencję wymaganą do oceny popytu i podaży, montażu części itp. AI jest wykorzystywana w biznesie e-commerce w dużym stopniu, aby zapewnić konkurencję dla branży e-commerce . Pomaga swoim klientom znaleźć powiązane produkty o sugerowanym rozmiarze, kolorze lub marce. Chatboty są wykorzystywane na stronach firm, aby zapewnić niemal natychmiastową obsługę klienta. Na przykład McDonald’s wykorzystuje sztuczną inteligencję do analizowania trendów zamówień klientów. Co więcej, klienci mogą składać zamówienia bezpośrednio, korzystając z kiosków lub terminali interaktywnych, zamiast zajmować się kasjerem na żywo; zmniejszyło to liczbę błędów w zamówieniach i zwiększyło sprzedaż.
6. Bezpieczeństwo danych: w świecie cyfrowym cyberataki rosną bardzo szybko, a bezpieczeństwo danych stało się kluczowe dla wszystkich organizacji. Sztuczna inteligencja służy do zwiększania bezpieczeństwa tych danych. Sztuczna inteligencja i ML w produktach z zakresu cyberbezpieczeństwa zapewniają wartość dodaną w identyfikowaniu ataków złośliwego oprogramowania. Sztuczna inteligencja jest w stanie ocenić nowe ataki szkodliwego oprogramowania znacznie szybciej niż operatorzy. Oparta na sztucznej inteligencji technologia bezpieczeństwa zapewnia organizacjom zaawansowane informacje umożliwiające podjęcie środków ostrożności przed zagrożeniami, zanim wystąpią rzeczywiste szkody. Technologia, taka jak bot AEG czy platforma AI2, odgrywa ważną rolę w pomaganiu organizacjom w walce z cyberatakami; mogą być również wykorzystywane do wykrywania błędów oprogramowania, które umożliwiają cyberataki.
7. Edukacja: sztuczna inteligencja może dostosować uczenie się zgodnie z wymaganiami każdego ucznia i zapewnić dobre wrażenia z nauki. Ponadto zapewnia powszechny dostęp wszystkim studentom, a także pomaga im pracować we własnym tempie. System automatyzuje również systemy oceniania egzaminów poprzez zmniejszenie zaangażowania edukatorów, dając im więcej czasu na nauczanie. Chatbot AI, jako asystent nauczyciela, może skutecznie komunikować się z uczniami. Opiekun AI może uczyć przedmiotu zgodnie z wymaganiami uczniów. Sztuczna inteligencja może w przyszłości działać jako osobisty wirtualny nauczyciel dla studentów, który będzie łatwo dostępny dla studentów w dowolnym miejscu i czasie.
8. Rozrywka: aplikacje oparte na sztucznej inteligencji, takie jak Netflix czy Amazon, świadczą usługi rozrywkowe na całym świecie. Za pomocą algorytmów sztucznej inteligencji opartych na ML usługi te polecają również użytkownikom określone programy lub programy.
9. Finanse: Aplikacje finansowe wymagają gromadzenia danych osobowych osób fizycznych i zapewniają pomoc, porady i sugestie związane z finansami, a nawet mogą pomóc w obrocie papierami wartościowymi. Dziś handel na Wall Street odbywa się za pomocą oprogramowania AI. Branże finansowe wykorzystują ML w automatyzacji, chatbocie, inteligencji adaptacyjnej, handlu algorytmami itp. w procesach finansowych. Systemy sztucznej inteligencji, takie jak Intuit Mint czy TurboTax, są wykorzystywane przez instytucje finansowe do osobistych aplikacji finansowych, podczas gdy inne programy, takie jak IBM Watson, są wykorzystywane do kupowania domów.
10. Gry: Sztuczna inteligencja może być wykorzystywana do celów gier do generowania alternatywnych rozwiązań w grze na podstawie decyzji podejmowanych przez użytkowników w grze, takich jak ruchy gracza, odnajdywanie ścieżek itp. Programowanie oparte na sztucznej inteligencji jest obecnie używane w wielu grach wideo, takie jak Minecraft i Tom Clancy’s Splinter Cell. Maszyny AI mogą odgrywać kluczową rolę w grach, takich jak poker, szachy itp.
11. Rząd: Rządy wykorzystują sztuczną inteligencję do opracowywania odpowiednich polityk i usług, analizowania wypadków drogowych i znajdowania rozwiązań wielu innych problemów. Aplikacje oparte na sztucznej inteligencji zmniejszają koszty, minimalizują błędy, przejmują duże obciążenia i pomagają rozładować zaległości.
12. Opieka zdrowotna: AI pomaga lekarzom na wiele sposobów i zapewnia szybszy powrót do zdrowia pacjentów. Sztuczna inteligencja może pomóc lekarzom i pacjentom w diagnozowaniu i informowaniu pacjentów o najnowszych stanach chorobowych, a jeśli stan jest poważny, zapewnia szybsze dotarcie pomocy medycznej do pacjentów. Sztuczna inteligencja ma kilka zalet i oczekuje się, że będzie miała pozytywny wpływ na branżę opieki zdrowotnej. Opracowywane są roboty AI, które będą w stanie opiekować się osobami starszymi i przypominać im o zażyciu leków, a nawet lokalizować zagubione przedmioty, takie jak okulary. Różne aplikacje AI mogą obejmować korzystanie przez pacjentów z wirtualnych asystentów medycznych i chatbotów online, zbieranie historii medycznej, ustalanie wizyt i pomoc w zadaniach administracyjnych. Technologie sztucznej inteligencji są również pomocne w zrozumieniu pandemii, takich jak COVID-19. Na przykład kanadyjska firma BlueDot wykorzystała technologię sztucznej inteligencji do wykrycia epidemii COVID-19 w Wuhan w Chinach wkrótce po wykryciu kilku pierwszych przypadków. IBM Watson potrafi zrozumieć język naturalny i udzielać odpowiedzi na zapytania. System może przeszukiwać dane pacjentów w celu opracowania ram do prezentacji wyników ze względną punktacją. Ale chociaż algorytmy predykcyjne mogą być pomocne w kontrolowaniu pandemii lub innych globalnych zagrożeń, ostateczny wpływ sztucznej inteligencji jest niemożliwy do przewidzenia. Wiadomo, że roboty coraz częściej pomagają chirurgom na sali operacyjnej. Wyspecjalizowane roboty są produkowane do przeprowadzania eksperymentów i zapewniania realistycznych doświadczeń bez przeprowadzania jakichkolwiek praktycznych eksperymentów na pacjentach. Na przykład Gaumard, firma zajmująca się edukacją zdrowotną, produkuje obecnie roboty, które mogą być wykorzystywane do przeprowadzania różnych eksperymentów przez studentów medycyny i lekarzy w celu praktycznej nauki. Te realistyczne roboty mogą wchodzić w interakcje z opiekunami i symulować mimikę twarzy i inne fizyczne reakcje na pytania i działania lekarzy lub studentów medycyny, gdy zostaną o to poproszone, porozmawiane lub dotknięte. Pracownicy medyczni mogą nie tylko wchodzić w interakcje z robotami, ale można również obsługiwać roboty, aby uczyć procedury, a także podejmować kroki naprawcze w przypadku popełnienia jakichkolwiek błędów podczas operacji. Korzystając z takiego systemu opartego na sztucznej inteligencji, studenci medycyny mogą z łatwością wykonywać nacięcia, przeprowadzać operacje, pobierać krew, monitorować oddech itp.
13. Prawo: Wykorzystanie AI okazuje się oszczędzać czas, aby zautomatyzować pracochłonne procesy branży prawniczej, a tym samym przyczynić się do poprawy usług klientów. Firmy prawnicze i specjaliści wykorzystują sztuczną inteligencję opartą na ML do analizowania danych i przewidywania wyników. Ponadto do wydobywania informacji służy wizja komputerowa, a NLP służy do interpretowania żądań informacji.
14. Przetwarzanie języka naturalnego: NLP wykorzystuje możliwości maszyn do rozumienia języków naturalnych. Dwa z najczęściej używanych przykładów NLP, dostępnych w wielu smartfonach i oprogramowaniu komputerowym, to sprawdzanie pisowni i autokorekta. W 2019 roku dwie AI stworzone przez Alibaba i Microsoft pokonały zespół osób w teście czytania ze zrozumieniem Stanforda. Algorytmy mogły „przeczytać” serię wpisów z Wikipedii na ten temat i skutecznie odpowiedzieć na szereg pytań dotyczących tego tematu dokładniej niż ludzie.
15. Osobisty asystent: osobisty asystent oparty na sztucznej inteligencji może wykonywać kilka zadań na podstawie poleceń ustnych lub pisemnych, takich jak nawigacja w zapisach lub ocena, czy dana osoba doznała zawału serca podczas połączeń alarmowych. To dobry przykład słabej AI, ponieważ algorytm został stworzony do wykonania określonego zadania. Najbardziej znanymi przykładami asystentów AI są Google, Alexa i Siri (Kowalewskisays, 2019). Jednym z najbardziej korzystnych punktów dotyczących asystenta AI jest to, że służy on jako świetna pomoc w różnych zastosowaniach AI. Ponieważ coraz więcej konsumentów korzysta z wirtualnych asystentów osobistych, rozpoznawanie mowy stało się niezbędne w naszym życiu. Telefony, komputery i sprzęt AGD zwiększają naszą zależność od AI i ML poprzez głos. Według najnowszych statystyk rynek asystentów AI będzie się dalej rozwijał i do 2025 r. będzie wart 25 miliardów dolarów.
16. Robotyka: sztuczna inteligencja odgrywa niezwykłą rolę w robotyce. Branże produkcyjne dostosowują się do włączenia robotów do swoich przepływów pracy. Wcześniej roboty przemysłowe zostały oddzielone od pracowników ludzkich i zaprogramowane do wykonywania pojedynczych zadań. Dziś roboty przemysłowe funkcjonują jako coboty, które są mniejszymi i wielozadaniowymi robotami. Takie coboty mogą być wykorzystywane do wykonywania zadań w magazynach, przemyśle i innych miejscach pracy. Zwykle roboty są zaprogramowane do wykonywania zadań, które mają charakter powtarzalny, ale roboty oparte na sztucznej inteligencji są używane do wykonywania kilku zadań z własnym wcześniejszym doświadczeniem, a nawet bez wcześniejszego programowania. Roboty humanoidalne są najlepszymi przykładami inteligentnych robotów opartych na sztucznej inteligencji; tak jak Erica i Sophia potrafią mówić i zachowywać się jak ludzie. Ich czujniki mogą wykrywać dane fizyczne ze świata rzeczywistego, takie jak światło, dźwięk, temperatura, ruch i ciśnienie, a systemy te mogą uczyć się na podstawie swojej przeszłości i stosować tę wiedzę w nowym środowisku . Roboty przemysłowe są wykorzystywane w branży produkcyjnej jako alternatywa dla ludzi. Na przykład takie roboty są używane w sektorze produkcji samochodów od dłuższego czasu, ponieważ niektóre procesy w produkcji samochodów mogą nie być bezpieczne dla ludzi. W 1961 r. Unimate, pierwszy robot przemysłowy, został wykorzystany przez General Motors na linii montażowej. Obecnie roboty są wykorzystywane w magazynach również do wielu innych zadań. W 2014 roku Amazon wdrożył w magazynach swoich centrów roboty Kiva, które pomagają pracownikom bardzo szybko realizować zamówienia (15 minut), którymi mogą zarządzać sami ludzie (90 minut). Roboty te mogą podnosić przedmioty i transportować zapasy bezpośrednio do pracowników. Zaprogramowane z technologią wykrywania obiektów, roboty te mogą swobodnie poruszać się po magazynie, unikając potencjalnych kolizji z innymi robotami Kiva lub pracownikami ludzkimi.
17. Media społecznościowe: sztuczną inteligencję można wykorzystać do efektywnego organizowania dużych ilości danych i zarządzania nimi. Serwisy społecznościowe, takie jak Facebook, Twitter i Snapchat, mogą zawierać profile dużej liczby użytkowników, które muszą być efektywnie przechowywane i zarządzane. Sztuczna inteligencja może analizować ten ogromny blok danych, aby zidentyfikować najnowsze trendy, hashtagi i wymagania, między innymi, różnych użytkowników.
18. Supermarkety (sprzedaż detaliczna): Niektóre duże branże w sektorze handlu detalicznego zaczęły używać robotów opartych na sztucznej inteligencji do wykonywania zadań wykonywanych wcześniej przez ludzkich współpracowników klientów. Zapasy magazynowe są zazwyczaj czasochłonne i wymagają wielu pracowników śledzenia towarów, które wymagają uzupełnienia, aby można było je ponownie zamówić. Kilka supermarketów i innych rynków detalicznych używa teraz robotów do inwentaryzacji. Na przykład Walmart, gigant branży detalicznej i Bossa Nova, firma zajmująca się robotyką, połączyły siły, aby stworzyć aplikację dla supermarketów. Robot Bossa Nova byłby używany do skanowania półek w czasie rzeczywistym w celu zbierania danych o produktach, robiąc to znacznie szybciej niż mógłby to zrobić człowiek. Taki robot ma na celu poprawę dostępności produktów, poprawę obsługi klienta i zmniejszenie obciążenia współpracowników klienta.
19. Transport i podróże: Zapotrzebowanie na sztuczną inteligencję rośnie również w branży turystycznej. Poza sztuczną inteligencją wykorzystywaną w pojazdach autonomicznych, służy do zarządzania ruchem, szacowania opóźnień lotów i wielu innych zadań. Jest również stosowany w sektorze ubezpieczeń turystycznych, aby szybciej i sprawniej zgłaszać roszczenia po wypadkach. Sztuczna inteligencja może być wykorzystywana do organizowania podróży i sugerowania swoim klientom zakwaterowania, lotów i najlepszych tras. Biura podróży wykorzystują chatboty oparte na sztucznej inteligencji w celu szybszej reakcji i lepszej obsługi swoich klientów.
20. Systemy wizyjne: Opracowywane są algorytmy oparte na wizji, aby przewidywać przyszłe działania jednostek. Widzenie maszynowe może przechwytywać i analizować informacje wizualne za pomocą kamery oraz przetwarzania wideo i sygnału cyfrowego. Systemy te mogą rozumieć, interpretować, analizować i wyświetlać wizualizacje. Na przykład lekarze mogą wykorzystać system ekspercki do operowania pacjentów. Policja może ich użyć do rozpoznawania twarzy przestępców na podstawie rysunków wykonanych przez kryminalistę.
21. Rozpoznawanie mowy: Niektóre systemy oparte na sztucznej inteligencji mogą być używane do słuchania i rozumienia zdań oraz ich znaczenia, gdy osoba mówi. Systemy te są w stanie poradzić sobie z różnymi akcentami, slangiem, hałasem w tle, zmianami w głosie osoby z powodu choroby i wieloma innymi aspektami.
22. Rozpoznawanie pisma ręcznego: Algorytm jest w stanie odczytać tekst napisany na papierze za pomocą długopisu lub na ekranie za pomocą rysika. Ponadto potrafi również rozpoznawać kształty liter i konwertować je na tekst do edycji

Kolejną klasą mechanizmów, którym się przyglądamy, są procedury głosowania, które są używane do podejmowania decyzji politycznych w społeczeństwach demokratycznych. Badanie procedur głosowania wywodzi się z dziedziny teorii wyboru społecznego.

Podstawowe ustawienie jest następujące. Jak zwykle mamy zbiór N = {1,…,n} agentów, którzy w tym dziale będą wyborcami. Wyborcy ci chcą podejmować decyzje w odniesieniu do zbioru Ω = {ω₁,ω₂,…} możliwych wyników. W wyborach politycznych każdy element W może reprezentować innego kandydata, który wygrywa wybory. Każdy wyborca ​​będzie miał preferencje nad Ω. Zazwyczaj wyraża się je nie jako użyteczność ilościową, ale raczej jako jakościowe porównania: piszemy 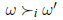oznacza ten wynik ω  jest w rankingu powyżej wyniku ω’ według agenta i. W wyborach z trzema kandydatami agent i może mieć 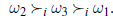Podstawowym problemem teorii wyboru społecznego jest połączenie tych preferencji za pomocą funkcji dobrobytu społecznego w celu uzyskania porządku preferencji społecznych: rankingu kandydatów, od najbardziej preferowanych do najmniej preferowanych. W niektórych przypadkach interesuje nas tylko wynik społeczny – najbardziej preferowany przez grupę jako całość. Będziemy pisać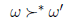

oznacza, że ​​ω znajduje się powyżej ω’ w kolejności preferencji społecznych. Prostsze ustawienie to sytuacja, w której nie chodzi nam o uzyskanie całej kolejności kandydatów, ale po prostu chcemy wybrać zestaw zwycięzców. Funkcja wyboru społecznego przyjmuje jako dane wejściowe kolejność preferencji dla każdego wyborcy, a jako dane wyjściowe tworzy zbiór zwycięzców. Społeczeństwa demokratyczne chcą wyniku społecznego, który odzwierciedla preferencje wyborców. Niestety nie zawsze jest to proste. Rozważmy Paradoks Condorceta, słynny przykład przedstawiony przez markiza de Condorcet (1743-1794). Załóżmy, że mamy trzy wyniki, Ω = {ω_a,ωb,ω_c} i trzech wyborców, N = {1,2,3}, z następującymi preferencjami. 

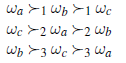
Załóżmy teraz, że musimy wybrać jednego z trzech kandydatów na podstawie tych preferencji. Paradoks polega na tym, że:

• 2=3 głosujących preferuje ω₃ nad ω₁.
• 2=3 głosujących preferuje ω₁ nad ω₂.
• 2=3 głosujących preferuje ω₂ nad ω₃.

Tak więc dla każdego możliwego zwycięzcy możemy wskazać innego kandydata, którego preferowałyby co najmniej 2/3 elektoratu. To oczywiste, że w demokracji nie możemy liczyć na zadowolenie każdego wyborcy. To pokazuje, że istnieją scenariusze, w których niezależnie od tego, jaki wynik wybierzemy, większość głosujących będzie wolała inny wynik. Naturalnym pytaniem jest, czy istnieje jakakolwiek „dobra” procedura wyboru społecznego, która naprawdę odzwierciedla preferencje wyborców. Aby na to odpowiedzieć, musimy sprecyzować, co mamy na myśli, gdy mówimy, że reguła jest „dobra”. Wymienimy niektóre właściwości, które chcielibyśmy, aby spełniała dobra funkcja dobrobytu społecznego:

• Warunek Pareto: Warunek Pareto mówi po prostu, że jeśli każdy głosujący ma pozycję ω_i powyżej ω_j, to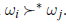

• Warunek zwycięzcy programu Condorcet: wynik jest uważany za zwycięzcę programu Condorcet, jeśli większość kandydatów woli go od wszystkich innych wyników. Innymi słowy, zwycięzca Condorceta to kandydat, który pokonałby każdego innego kandydata w wyborach parami. Warunek zwycięzcy Condorcet mówi, że jeśli ω_i jest zwycięzcą Condorcet, to ω_i powinno zająć pierwsze miejsce.

• Niezależność od nieistotnych alternatyw (IIA): Załóżmy, że jest wielu kandydatów, w tym ω_i i ω_j, a preferencje wyborców są takie, że 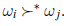  Załóżmy teraz, że jeden głosujący zmienił w jakiś sposób swoje preferencje, ale nie w odniesieniu do względnego rankingu ω_i oraz ω_j. Warunek IIA mówi, że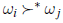

nie powinno się zmieniać.

• Brak dyktatur: Nie powinno być tak, że funkcja opieki społecznej po prostu przedstawia preferencje jednego wyborcy i ignoruje wszystkich innych wyborców.

Te cztery warunki wydają się rozsądne, ale podstawowe twierdzenie teorii wyboru społecznego zwane twierdzeniem Arrowa (ze względu na Kennetha Arrowa) mówi nam, że spełnienie wszystkich czterech warunków jest niemożliwe (w przypadkach, w których są co najmniej trzy wyniki). Oznacza to, że dla jakikolwiek mechanizm wyboru społecznego, który zechcemy wybrać, pojawią się sytuacje (być może nietypowe lub patologiczne), które doprowadzą do kontrowersyjnych wyników. Nie oznacza to jednak, że demokratyczne podejmowanie decyzji jest w większości przypadków beznadziejne. Nie widzieliśmy jeszcze żadnych rzeczywistych procedur głosowania, więc przyjrzyjmy się teraz niektórym.

• Przy zaledwie dwóch kandydatach głosowanie zwykłą większością (standardowa metoda w USA i Wielkiej Brytanii) jest preferowanym mechanizmem. Pytamy każdego wyborcę, którego z dwóch kandydatów preferuje, a ten z największą liczbą głosów jest zwycięzcą.

• W przypadku więcej niż dwóch wyników głosowanie wieloosobowe jest powszechnym systemem. Pytamy każdego wyborcę o jego najlepszy wybór i wybieramy kandydata(ów) (więcej niż jednego w przypadku remisu), który otrzyma najwięcej głosów, nawet jeśli nikt nie uzyska większości. Chociaż jest to powszechne, głosowanie pluralistyczne jest krytykowane za dostarczanie niepopularnych wyników. Kluczowym problemem jest to, że uwzględnia tylko najwyżej sklasyfikowanego kandydata w preferencjach każdego wyborcy.
• Licznik Borda (po Jean-Charles de Borda, współczesnym rywalu Condorceta) to procedura głosowania, która uwzględnia wszystkie informacje w kolejności preferencji wyborcy. Załóżmy, że mamy k kandydatów. Następnie dla każdego wyborcy i ustalamy jego preferencje w kolejności i i przyznajemy wynik k pierwszemu kandydatowi w rankingu, wynik k􀀀1 kandydatowi na drugim miejscu i tak dalej aż do najmniej uprzywilejowanego kandydata w zamawiam. Całkowity wynik dla każdego kandydata to ich liczba Borda, a aby uzyskać wynik społeczny , wyniki są uporządkowane według ich liczby Borda — od najwyższego do najniższego. Jednym z praktycznych problemów tego systemu jest to, że wymaga on od wyborców wyrażenia preferencji dotyczących wszystkich kandydatów, a niektórych wyborców może obchodzić tylko podzbiór kandydatów.
• W głosowaniu zatwierdzającym wyborcy zgłaszają podzbiór kandydatów, których aprobują. Zwycięzcami są ci, którzy zostali zatwierdzeni przez największą liczbę głosujących. Ten system jest często używany, gdy zadaniem jest wyłonienie wielu zwycięzców.
• W natychmiastowej drugiej turze głosowania wyborcy klasyfikują wszystkich kandydatów, a jeśli kandydat ma większość głosów pierwszego miejsca, zostają ogłoszeni zwycięzcą. Jeśli nie, kandydat z najmniejszą liczbą głosów pierwszego miejsca zostaje wyeliminowany. Ten kandydat jest usuwany ze wszystkich rankingów preferencji (a więc ci wyborcy, którzy wyeliminowali kandydata jako pierwszy wybór, mają teraz innego kandydata jako swój nowy pierwszy wybór) i proces jest powtarzany. W końcu jakiś kandydat będzie miał większość głosów pierwszego miejsca (chyba że jest remis).
• W głosowaniu na zasadzie prawdziwej większości zwycięzcą jest kandydat, który pokona każdego innego kandydata w porównaniach parami. Wyborcy proszeni są o pełny ranking preferencji wszystkich kandydatów. Tak mówimy! bije !0, jeśli więcej wyborców ma ! !0 niż mieć !0!. Ten system ma tę przyjemną właściwość, że większość zawsze zgadza się na zwycięzcę, ale ma tę złą właściwość, że nie wszystkie wybory będą rozstrzygane: na przykład w paradoksie Condorceta żaden kandydat nie wygrywa większości.

Inteligentne gadżety mogą sprawić, że codzienne zadania będą proste i szybkie. Na przykład Alexa jest w stanie prowadzić rejestr naszych codziennych spotkań, listę przedmiotów do kupienia, odtwarzać wybraną muzykę, czytać wiadomości i grać w innowacyjne gry. Oto kilka innych przykładów:

1. Echo: Echo, uruchomione przez Amazon, to asystent głosowy w chmurze, Alexa. Jest w stanie słyszeć, rozumieć i odpowiadać na polecenia lub pytania użytkowników i oferować możliwe rozwiązania. Na przykład możesz zapytać Alexę, czy potrzebujesz parasola przed wyjściem, i może to zasugerować, żebyś go wziął, ponieważ po południu może padać.
2. Flipkart: Flipkart, platforma zakupów e-commerce, może być używana do sugerowania produktów swoim klientom na podstawie ich przeszłych zakupów lub historii przeglądania przedmiotów.
3. Pandora: Platforma Pandora wykorzystuje sztuczną inteligencję do określania muzyki, której potrzebują użytkownicy. Nie daje jednak możliwości wyboru utworów.
4. Netflix: Netflix jest obecnie najpopularniejszą platformą Over The Top (OTT), znaną również jako platforma Other Than Television, do której należą Amazon Prime, Hulu i inne. Platformy OTT świadczą usługi, które dostarczają treści swoim klientom przez Internet, płacąc opłatę abonamentową. Zalecają również dodatkowe treści na podstawie wcześniejszych wyborów użytkownika.

5. Siri: Opracowany przez Apple, Siri to interaktywny asystent aktywowany głosem. Wykorzystuje technologię ML, aby zrozumieć, w jaki sposób użytkownicy poruszają się po swoich telefonach, wysyłają wiadomości i wykonują połączenia telefoniczne. Aby skorzystać z tej funkcji, zacznij od powiedzenia „Hello Siri”, a następnie żądania działania.

Rozważmy teraz inny rodzaj gry, w której kraje ustalają swoją politykę kontrolowania zanieczyszczenia powietrza. Każdy kraj ma wybór: mogą zmniejszyć zanieczyszczenie kosztem -10 punktów za wdrożenie niezbędnych zmian lub mogą nadal zanieczyszczać, co daje im użyteczność netto -5 (w dodanych kosztach zdrowia itp.), a także dodaje -1 punktów każdemu innemu krajowi (ponieważ powietrze jest dzielone między kraje). Oczywiście dominującą strategią dla każdego kraju jest „kontynuowanie zanieczyszczania”, ale jeśli jest 100 krajów i każdy postępuje zgodnie z tą polityką, wówczas każdy kraj uzyskuje całkowitą użyteczność wynoszącą -104, podczas gdy jeśli każdy kraj zmniejszyłby zanieczyszczenie, każdy z nich miałby użyteczność -10. Ta sytuacja nazywana jest tragedią wspólnego dobra: jeśli nikt nie musi płacić za korzystanie ze wspólnego zasobu, może on zostać wykorzystany w sposób, który prowadzi do niższej ogólnej użyteczności dla wszystkich agentów. Jest to podobne do dylematu więźnia: istnieje inne rozwiązanie gry, które jest lepsze dla wszystkich stron, ale wydaje się, że racjonalni agenci nie mogą znaleźć takiego rozwiązania w obecnej grze. Jednym ze sposobów radzenia sobie z tragedią wspólnego dobra jest zmiana mechanizmu na taki, który obciąża każdego agenta za korzystanie z tego wspólnego. Mówiąc bardziej ogólnie, musimy zapewnić, że wszystkie efekty zewnętrzne – wpływy na globalną użyteczność, które nie są rozpoznawane w transakcjach poszczególnych agentów – są jasno określone. Prawidłowe ustalenie cen to trudna część. Podejście to sprowadza się do stworzenia mechanizmu, w którym każdy agent jest faktycznie wymagany do maksymalizacji globalnej użyteczności, ale może to zrobić, podejmując lokalną decyzję. W tym przykładzie podatek węglowy byłby przykładem mechanizmu, który pobiera opłaty za korzystanie z dóbr wspólnych w sposób, który, jeśli zostanie dobrze wdrożony, maksymalizuje globalną użyteczność.

Okazuje się, że istnieje konstrukcja mechanizmu, znana jako mechanizm Vickrey-Clarke-Groves lub VCG, który ma dwie korzystne właściwości. Po pierwsze, jest to maksymalizacja użyteczności – to znaczy maksymalizuje użyteczność globalną, która jest sumą użyteczności dla wszystkich stron, Σ_iv_i. Po drugie, mechanizm polega na ujawnianiu prawdy – dominującą strategią wszystkich agentów jest ujawnianie ich prawdziwej wartości. Nie muszą angażować się w skomplikowane kalkulacje licytacji strategicznych. Podamy przykład wykorzystując problem alokacji niektórych dóbr wspólnych. Załóżmy, że miasto zdecyduje, że chce zainstalować bezpłatne bezprzewodowe urządzenia nadawczo-odbiorcze do Internetu. Jednak liczba dostępnych nadajników-odbiorników jest mniejsza niż liczba dzielnic, które ich potrzebują. Miasto chce zmaksymalizować globalną użyteczność, ale jeśli powie każdej radzie sąsiedzkiej: „Ile cenisz darmowy nadajnik-odbiornik (a przy okazji oddamy go stronom, które cenią je najbardziej)?” wtedy każda dzielnica będzie miała motywację do zgłoszenia bardzo wysokiej wartości. Mechanizm VCG zniechęca do tej sztuczki i daje im motywację do zgłaszania ich prawdziwej wartości. Działa w następujący sposób:

1. Centrum prosi każdego agenta o zgłoszenie wartości przedmiotu, v_i.
2. Centrum przydziela towary do zestawu zwycięzców,W, aby zmaksymalizować Σ_iεW v_i.
3. Centrum oblicza dla każdego zwycięskiego agenta, jaką stratę spowodowała jego indywidualna obecność w grze u przegranych (z których każdy otrzymał 0 użyteczności, ale mógłby otrzymać v_j, gdyby był zwycięzcą).
4. Każdy zwycięski agent płaci następnie do centrum podatek równy tej stracie.

Załóżmy na przykład, że dostępne są 3 transceivery i 5 licytujących, którzy licytują 100, 50, 40, 20 i 10. Zatem zestaw 3 zwycięzców, W, to ci, którzy licytują 100, 50 i 40, a globalna użyteczność od przydzielenia tych dóbr wynosi 190. W przypadku każdego zwycięzcy, gdyby nie był w grze, zwycięzcą byłaby oferta 20. W ten sposób każdy zwycięzca płaci do centrum podatek w wysokości 20. Wszyscy zwycięzcy powinni być szczęśliwi, ponieważ płacą podatek niższy niż ich wartość, a wszyscy przegrani są tak szczęśliwi, jak tylko mogą, ponieważ wyceniają towary mniej niż wymagany podatek. Dlatego mechanizm ujawnia prawdę. W tym przykładzie kluczowa wartość to 20; byłoby irracjonalne licytować powyżej 20, jeśli twoja prawdziwa wartość była w rzeczywistości poniżej 20 i na odwrót. Ponieważ kluczową wartością może być dowolna (w zależności od innych oferentów), oznacza to, że licytowanie czegokolwiek innego niż Twoja prawdziwa wartość jest zawsze irracjonalne. Mechanizm VCG jest bardzo ogólny i można go zastosować do wszelkiego rodzaju gier, nie tylko aukcji, z lekkim uogólnieniem opisanego powyżej mechanizmu. Na przykład w aukcji kombinatorycznej dostępnych jest wiele różnych przedmiotów, a każdy licytujący może złożyć wiele ofert, każda na podzbiór przedmiotów. Na przykład w licytacji działek jeden oferent może chcieć wybrać działkę X lub działkę Y, ale nie obie; inny może chcieć dowolnych trzech sąsiadujących działek i tak dalej. Mechanizm VCG można wykorzystać do znalezienia optymalnego wyniku, chociaż przy 2^N podzbiorach N dóbr, z którymi trzeba się zmagać, obliczenie optymalnego wyniku jest NPkompletne. Z kilkoma zastrzeżeniami mechanizm VCG jest wyjątkowy: każdy inny optymalny mechanizm jest zasadniczo równoważny.