Być może najprostszym i najbardziej znanym przykładem problemu bandytów jest bandyta Bernoulliego, w którym każde ramię Mi daje nagrodę w wysokości 0 lub 1 z ustalonym, ale nieznanym prawdopodobieństwem μi. Stan ramienia Mi jest zdefiniowany przez si i fi, dotychczasowe liczby sukcesów (1s) i niepowodzeń (0s) dla tego ramienia; prawdopodobieństwo przejścia przewiduje, że następny wynik będzie równy 1 z prawdopodobieństwem (si)=(si + fi) i 0 z prawdopodobieństwem ( fi)=(si + fi). Liczby są inicjowane na 1, więc początkowe prawdopodobieństwa wynoszą 1/2, a nie 0/0 Proces nagrody Markowa pokazano na rysunku (a).
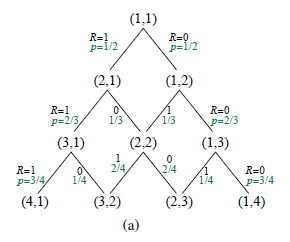
Nie możemy całkowicie zastosować transformacji z poprzedniej sekcji do obliczenia wskaźnika Gittinsa ramienia Bernoulliego, ponieważ ma nieskończenie wiele stanów. Możemy jednak uzyskać bardzo dokładne przybliżenie, rozwiązując obcięty MDP ze stanami do si + fi=100 i γ=0,9. Wyniki przedstawiono na rysunku (b).
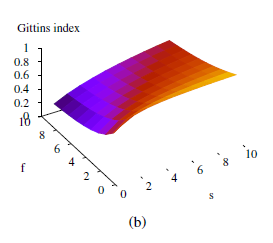
Wyniki są intuicyjnie rozsądne: widzimy, że ogólnie rzecz biorąc, preferowane są odmiany o wyższym prawdopodobieństwie wypłaty, ale istnieje również premia eksploracyjna związana z ramionami, które zostały wypróbowane tylko kilka razy. Premia eksploracyjna Na przykład wskaźnik dla stanu (3,2) jest wyższy niż wskaźnik dla stanu (7,4) (0,7057 vs 0,6922), mimo że szacowana wartość (3,2) jest niższa (0,6 w porównaniu do 0,6364).