Aby lepiej wyczuć indeks, obliczmy wartość licznika, mianownika i współczynnika w równaniu (16.15) dla różnych możliwych czasów zatrzymania w deterministycznej sekwencji nagrody 0,2,0,7,2,0;,0 ,0,…,
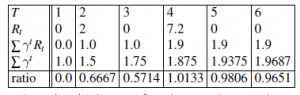
Oczywiście od tego momentu stosunek będzie się zmniejszał, ponieważ licznik pozostaje stały, podczas gdy mianownik nadal rośnie. Tak więc indeks Gittinsa dla tego ramienia wynosi 1,0133, maksymalna wartość osiągnięta przez wskaźnik. W połączeniu ze stałym ramieniem Mλ z 0 < λ ≤ 1,0133, optymalna polisa zbiera pierwsze cztery nagrody od M, a następnie przełącza się na Mλ . Dla λ > 1,0133 optymalna polityka zawsze wybiera Mλ . Aby obliczyć indeks Gittinsa dla ramienia ogólnego M przy obecnym stanie s, po prostu dokonujemy następującej obserwacji: w punkcie krytycznym, w którym optymalna polityka jest obojętna między wyborem ramienia M a wyborem ramienia stałego Mλ , wartość wyboru M wynosi tyle samo jak wartość wyboru nieskończonej sekwencji λ-nagród. Załóżmy, że powiększamy M tak, że w każdym stanie w M agent ma dwie możliwości: albo kontynuować z M jak poprzednio, albo zakończyć i otrzymać nieskończoną sekwencję λ-nagród.
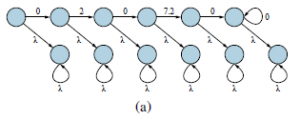
To zamienia M w MDP, którego optymalna polityka jest po prostu optymalną regułą zatrzymania dla M. Stąd wartość optymalnej polityki w tym nowym MDP jest równa wartości nieskończonej sekwencji λ-nagród, czyli λ/(1 – γ). Więc możemy po prostu rozwiązać ten MDP. . . ale niestety nie znamy wartości λ, jaką należy umieścić w MDP, ponieważ właśnie to próbujemy obliczyć. Wiemy jednak, że w punkcie krytycznym optymalna polityka jest obojętna między M i M , więc możemy zastąpić wybór uzyskania nieskończonej sekwencji λ-rewards wyborem powrotu i ponownego uruchomienia M od stanu początkowego s. (Dokładniej, dodajemy nową akcję w każdym stanie, która ma takie same nagrody i wyniki jak akcja dostępna w s.) Ten nowy MDP Ms, zwany restartem MDP, jest przedstawiony na rysunku (b).
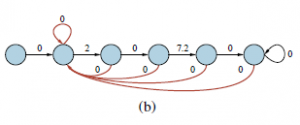
Mamy ogólny wynik, że indeks Gittinsa dla ramienia M w stanie s jest równy 1 razy wartość optymalnej polityki dla restartu MDP Ms. Ten MDP można rozwiązać za pomocą dowolnego algorytmu z wcześniejszej sekcji . Iteracja wartości zastosowana do Ms na rysunku (b) daje wartość 2,0266 dla stanu początkowego, więc mamy λ=2,0266 (1-γ)=1,0133 jak poprzednio.