W Las Vegas jednoręki bandyta jest automatem do gry. Gracz może wrzucić monetę, pociągnąć za dźwignię i odebrać wygrane (jeśli są). N-ręki bandyta ma n dźwigni. Za każdą dźwignią znajduje się stały, ale nieznany rozkład prawdopodobieństwa wygranych; każdy pobiera próbki z tej nieznanej dystrybucji. Hazardzista musi wybrać, jaką dźwignią zagrać na każdej kolejnej monecie – tej, która najbardziej się opłaciła, a może takiej, której jeszcze nie wypróbowano? To jest przykład wszechobecnego kompromisu między eksploatacją obecnie najlepszych działań w celu uzyskania nagród a eksploracją wcześniej nieznanych stanów i działaniami w celu uzyskania informacji, które w niektórych przypadkach można przekształcić w lepszą politykę i lepsze długoterminowe nagrody. W prawdziwym świecie nieustannie trzeba wybierać między kontynuowaniem wygodnej egzystencji, a wyruszeniem w nieznane w nadziei na lepsze życie. Problem n-rękich bandytów jest formalnym modelem rzeczywistych problemów w wielu niezwykle ważnych obszarach, takich jak decydowanie, które z n możliwych nowych sposobów leczenia choroby, które z n możliwych inwestycji, w które należy przeznaczyć część swoich oszczędności, n możliwych projektów badawczych do sfinansowania lub które z n możliwych reklam wyświetlić, gdy użytkownik odwiedza daną stronę internetową.
Wczesne prace nad tym problemem rozpoczęły się w USA podczas II wojny światowej; okazał się tak krnąbrny, że alianccy naukowcy zaproponowali, aby „problem zrzucić na Niemcy, jako ostateczne narzędzie intelektualnego sabotażu” . Okazuje się, że naukowcy, zarówno w czasie wojny, jak i po jej zakończeniu, próbowali udowodnić „oczywiście prawdziwe” fakty dotyczące problemów bandytów, które w rzeczywistości są fałszywe. Jak to ujął Bradt i inni: „Istnieje wiele fajnych właściwości, których optymalne strategie nie posiadają”. Na przykład, ogólnie zakładano, że optymalna polityka ostatecznie oprze się na najlepszym ramieniu w dłuższej perspektywie; w rzeczywistości istnieje skończone prawdopodobieństwo, że optymalna polityka będzie się opierać na części nieoptymalnej. Mamy teraz solidną wiedzę teoretyczną na temat problemów bandytów, a także przydatne algorytmy do ich rozwiązywania. Istnieje kilka różnych definicji problemów bandytów; jeden z najczystszych i najbardziej ogólnych to:
* Każde ramię Mi to proces nagradzania Markowa lub MRP, czyli MDP z tylko jednym możliwym działaniem ai. Ma stany Si, model przejścia Pi(s’ |s,ai) i nagrodę Ri(s,ai,s’). Ramię określa rozkład w sekwencjach nagród Ri,0,Ri,1,Ri,2,…, gdzie każdy Ri,t jest zmienną losową.
- Ogólnym problemem bandytów jest MDP: przestrzeń stanów jest dana przez iloczyn kartezjański S=S1 x … x Sn; akcje to a1,…,an jakiś; model przejściowy aktualizuje stan wybranego ramienia Mi, zgodnie z jego konkretnym modelem przejściowym, pozostawiając pozostałe ramiona niezmienione; a współczynnik dyskontowy to γ.
Ta definicja jest bardzo ogólna i obejmuje szeroki zakres przypadków. Kluczową właściwością jest to, że ramiona są niezależne, połączone tylko faktem, że agent może jednocześnie pracować tylko na jednym ramieniu. Możliwe jest zdefiniowanie jeszcze bardziej ogólnej wersji, w której ułamkowe wysiłki można zastosować do wszystkich ramion jednocześnie, ale łączny wysiłek we wszystkich ramionach jest ograniczony; podstawowe wyniki opisane tutaj przenoszą się na ten przypadek. Wkrótce zobaczymy, jak sformułować typowy problem bandytów w tych ramach, ale rozgrzejmy się prostym szczególnym przypadkiem deterministycznych sekwencji nagród. Niech γ=0:5 i załóżmy, że istnieją dwa ramiona oznaczone M i M1. Wielokrotne ciągnięcie M daje sekwencję nagród 0,2,0,7,2,0,0, …, podczas gdy ciągnięcie M1 daje 1,1,1,…,
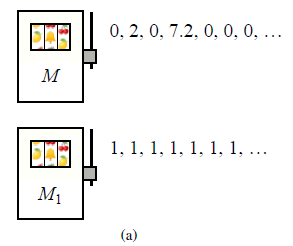
Gdyby na początku trzeba było zobowiązać się do jednej lub drugiej gałęzi i trzymać się jej, wybór zostałby dokonany poprzez obliczenie użyteczności (całkowita zdyskontowana nagroda) dla każdej odmiany:
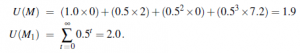
Można by pomyśleć, że najlepszym wyborem jest wybór M1, ale chwila zastanowienia pokazuje, że rozpoczęcie od M, a następnie przejście do M1 po czwartej nagrodzie daje sekwencję S=0,2,0,7,2,1,1, 1,…,, dla którego
![]()
Dlatego strategia S, która we właściwym czasie przechodzi z M do M1 jest lepsza niż każda z odmian osobno. W rzeczywistości S jest optymalny dla tego problemu: wszystkie inne czasy przełączania dają mniejszą nagrodę. Uogólnijmy nieco ten przypadek, aby teraz pierwsze ramię M dało dowolną sekwencję R0,R1,R2,… (które może być znane lub nieznane), a drugie ramię Mλ oddaje λ,λ,λ, … dla pewnej znanej stałej stałej λ .
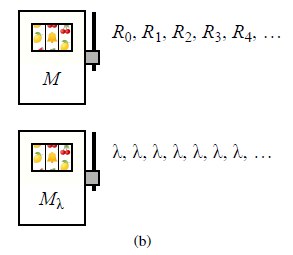
W literaturze nazywa się to jednorękim bandytą, ponieważ formalnie jest to odpowiednik przypadku, w którym istnieje jedno ramię M, które wytwarza nagrody R0 ,R1,R2, … i koszty λ za każde pociągnięcie. (Pociągnięcie ramienia M jest równoznaczne z nieciągnięciem Mλ , więc za każdym razem rezygnuje z nagrody.) Mając tylko jedno ramię, jedynym wyjściem jest czy pociągnąć ponownie, czy przestać. Jeśli pociągniesz pierwsze ramię T razy (tzn. w chwilach 0,1,…,T – 1 mówimy, że czas zatrzymania to T. Czas zatrzymania Wracając do naszej wersji z M i Mλ , załóżmy, że po T ciągnie pierwszą rękę, optymalna strategia ostatecznie ciągnie drugą rękę po raz pierwszy. Ponieważ z tego ruchu nie uzyskuje się żadnych informacji (już wiemy, że wypłata będzie λ ), w momencie T+1 będziemy w tym samym sytuacji, a zatem optymalna strategia musi dokonać tego samego wyboru. Równoważnie możemy powiedzieć, że optymalną strategią jest uruchomienie ramienia M do czasu T, a następnie przejście do Mλ przez resztę czasu. Możliwe, że T =0, jeśli strategia wybiera Mλ natychmiast lub T =∞ jeśli strategia nigdy nie wybiera M lub gdzieś pomiędzy. Rozważmy teraz wartość takiej λ, że optymalna strategia jest dokładnie obojętna między (a) uruchomieniem M aż do najlepszego możliwego zatrzymania czas, a następnie przełączenie na Mλ na zawsze i (b) natychmiastowe wybranie Mλ. W punkcie krytycznym mamy
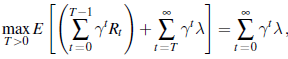
co upraszcza do
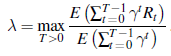
To równanie definiuje rodzaj „wartości” dla M pod względem jego zdolności do dostarczania strumienia nagród w odpowiednim czasie; licznik ułamka reprezentuje użyteczność, podczas gdy mianownik można traktować jako „zdyskontowany czas”, więc wartość opisuje maksymalną możliwą do uzyskania użyteczność na jednostkę zdyskontowanego czasu. (Ważne jest, aby pamiętać, że T w równaniu jest czasem zatrzymania, który jest regulowany przez regułę zatrzymania, a nie jest prostą liczbą całkowitą; redukuje się do prostej liczby całkowitej tylko wtedy, gdy M jest deterministyczną sekwencją nagrody.) Wartość zdefiniowana w Równanie nazywa się indeksem Gittinsa M. Niezwykłą cechą indeksu Gittinsa jest to, że zapewnia bardzo prostą, optymalną politykę dla każdego problemu z bandytami: pociągnij ramię, które ma najwyższy indeks Gittinsa, a następnie zaktualizuj indeksy Gittinsa J. Ponadto, ponieważ indeks ramienia Mi zależy tylko od właściwości tego ramienia, optymalną decyzję dotyczącą pierwszej iteracji można obliczyć w czasie O(n), gdzie n jest liczbą ramion. A ponieważ indeksy Gittinsa ramion, które nie zostały wybrane, pozostają niezmienione, każdą decyzję po pierwszej można obliczyć w czasie O(1).