Iteracja wartości i iteracja polityki to algorytmy offline: podobnie jak algorytm A* w rozdziale 3 generują optymalne rozwiązanie problemu, które może być następnie wykonane przez prostego agenta. W przypadku wystarczająco dużych MDP, takich jak Tetris MDP z 1062 stanami, dokładne rozwiązanie offline, nawet za pomocą algorytmu wielomianowego, nie jest możliwe. Opracowano kilka technik przybliżonego rozwiązania MDP w trybie offline. W tym miejscu rozważymy algorytmy online, analogiczne do tych używanych w grach , w których agent wykonuje znaczną ilość obliczeń w każdym punkcie decyzji, zamiast operować głównie na podstawie wcześniej obliczonych informacji. Najprostszym podejściem jest w rzeczywistości uproszczenie algorytmu EXPECTIMINIMAX dla drzew gier z węzłami losowymi: algorytm EXPECTIMAX buduje drzewo naprzemiennych węzłów maksymalnych i losowych, jak pokazano na rysunku.
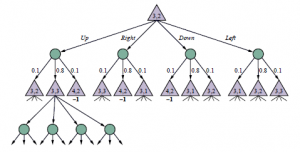
(Istnieje niewielka różnica w stosunku do standardowego EXPECTIMINIMAX w tym, że istnieją nagrody za przejścia nieterminalne i terminalne). Funkcję oceny można zastosować do nieterminalnych liści drzewa lub można im nadać wartość domyślną. Decyzję można wydobyć z drzewa poszukiwań, tworząc kopię zapasową wartości użyteczności z liści, biorąc średnią w węzłach szansy i biorąc maksimum w węzłach decyzyjnych.
W przypadku problemów, w których współczynnik dyskontowania γ nie jest zbyt bliski 1, przydatna jest koncepcja ε-horyzont. Niech ε będzie pożądanym ograniczeniem błędu bezwzględnego w narzędziach obliczonych z drzewa expectimax o ograniczonej głębokości, w porównaniu z dokładnymi narzędziami w MDP. Wtedy ε-horyzont to głębokość drzewa H tak, że suma nagród poza dowolnym liściem na tej głębokości jest mniejsza niż ε– ogólnie rzecz biorąc, wszystko, co dzieje się po H, jest nieistotne, ponieważ jest tak odległe w przyszłości. Ponieważ suma nagród poza H jest ograniczona przez γHRmax=(1- γ), głębokość z H=[logγε(1- γ)/Rmaxe] jest wystarczające. Tak więc zbudowanie drzewa na taką głębokość daje prawie optymalne decyzje. Na przykład przy γ=0:5, ε=0:1 i Rmax=1, znajdujemy H=5, co wydaje się rozsądne. Z drugiej strony, jeśli γ=0:9, H=44, co wydaje się mniej rozsądne! Oprócz ograniczania głębokości, możliwe jest również uniknięcie potencjalnie ogromnego współczynnika rozgałęzień w węzłach losowych. (Na przykład, jeśli wszystkie prawdopodobieństwa warunkowe w modelu przejścia DBN są niezerowe, prawdopodobieństwa przejścia, które są podane przez iloczyn prawdopodobieństw warunkowych, są również niezerowe, co oznacza, że każdy stan ma pewne prawdopodobieństwo przejścia do każdego innego stanu. ) Oczekiwania w odniesieniu do rozkładu prawdopodobieństwa P można aproksymować, generując N próbek z P i używając średniej próbki. W formie matematycznej mamy
![]()
Tak więc, jeśli współczynnik rozgałęzienia jest bardzo duży, co oznacza, że istnieje bardzo wiele możliwych wartości x, dobre przybliżenie wartości węzła szansy można uzyskać, próbując ograniczoną liczbę wyników działania. Zazwyczaj próbki skupiają się na najbardziej prawdopodobnych wynikach, ponieważ są one najbardziej prawdopodobne do wygenerowania. Jeśli przyjrzysz się uważnie drzewu na rysunku, zauważysz coś: tak naprawdę nie jest to drzewo. Na przykład korzeń (3,2) jest również liściem, więc należy traktować to jako wykres i ograniczyć wartość liścia (3,2) do wartości pierwiastka (3,2), ponieważ są to ten sam stan. W rzeczywistości ten sposób myślenia szybko sprowadza nas z powrotem do równań Bellmana, które wiążą wartości stanów z wartościami stanów sąsiednich. Zbadane stany faktycznie stanowią sub-MDP oryginalnego MDP, a ten sub-MDP można rozwiązać za pomocą dowolnego algorytmu w tym rozdziale, aby uzyskać decyzję dla bieżącego stanu. (Stany graniczne mają zwykle stałą szacunkową wartość. To ogólne podejście nazywa się programowaniem dynamicznym w czasie rzeczywistym (RTDP) i jest dość analogiczne do LRTA w Rozdziale 4. Algorytmy tego rodzaju mogą być całkiem skuteczne w domenach o umiarkowanej wielkości, takich jak światy gridowe ; w większych domenach, takich jak Tetris, są dwa problemy. Po pierwsze, przestrzeń stanów jest taka, że każdy możliwy do zarządzania zbiór eksplorowanych stanów zawiera bardzo mało powtarzających się stanów, więc równie dobrze można użyć prostego drzewa oczekiwanych. Po drugie, prosta heurystyka dla węzły graniczne mogą nie wystarczyć do prowadzenia agenta, zwłaszcza jeśli nagrody są nieliczne.
Jednym z możliwych rozwiązań jest zastosowanie uczenia się przez wzmacnianie w celu wygenerowania znacznie dokładniejszej heurystyki .Innym podejściem jest dalsze spojrzenie w MDP przy użyciu podejścia Monte Carlo. W rzeczywistości algorytm UCT z rysunku został pierwotnie opracowany dla MDP, a nie dla gier. Zmiany wymagane do rozwiązywania MDP, a nie gier, są minimalne: wynikają przede wszystkim z faktu, że przeciwnik (natura) jest stochastyczny i z potrzeby śledzenia nagród, a nie tylko wygranych i przegranych. W zastosowaniu do świata 4×3 osiągi UCT nie są specjalnie imponujące. Jak pokazuje Rysunek,
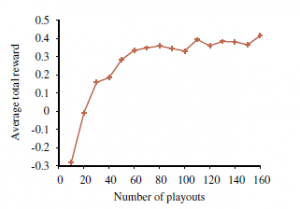
potrzeba średnio 160 odtworzeń, aby osiągnąć całkowitą nagrodę 0,4, podczas gdy optymalna polityka ma oczekiwaną całkowitą nagrodę 0,7453 od stanu początkowego (patrz Rysunek 16.3). Jednym z powodów, dla których UCT może mieć trudności, jest to, że buduje drzewo, a nie wykres i używa (w przybliżeniu) expectimax zamiast programowania dynamicznego. Świat 4×3 jest bardzo „zapętlony”: chociaż istnieje tylko 9 stanów nieterminalnych, playouty UCT często trwają ponad 50 akcji. UCT wydaje się lepiej pasować do Tetris, gdzie playouty idą na tyle daleko w przyszłość, aby dać agentowi poczucie, czy potencjalnie ryzykowny ruch w końcu zadziała, czy też spowoduje ogromne nagromadzenie. Szczególnie interesującym pytaniem jest, jak bardzo może pomóc prosta polityka symulacji – na przykład taka, która unika tworzenia nawisów i umieszcza elementy tak nisko, jak to możliwe.