Zauważono, że skala użyteczności jest arbitralna: transformacja afiniczna pozostawia niezmienioną decyzję optymalną. Możemy zastąpić U(s) przez U’(s) = mU(s)+b, gdzie m i b są dowolnymi stałymi takimi, że m > 0. Łatwo zauważyć, z definicji użyteczności jako zdyskontowanych sum nagród, że podobne transformacja nagród pozostawi optymalną politykę niezmienioną w MDP:
R’(s,a,s’) = mR(,a,s’)+b:
Okazuje się jednak, że addytywna dekompozycja nagrody użyteczności prowadzi do znacznie większej swobody w definiowaniu nagród. Niech Φ(s) będzie dowolną funkcją stanu s. Następnie, zgodnie z twierdzeniem o kształtowaniu, następująca transformacja pozostawia bez zmian optymalną politykę:
![]()
Aby pokazać, że to prawda, musimy udowodnić, że dwa programy MDP, M i M’, mają identyczne optymalne polityki, o ile różnią się tylko funkcjami nagrody, jak określono w równaniu . Zaczynamy od równania Bellmana dla Q, funkcji Q dla MDP M:
![]()
Teraz niech Q’(s,a)=Q(s,a)-Φ(s) i wstawić to do tego równania; dostajemy
![]()
co następnie upraszcza się do
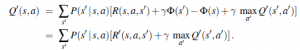
Innymi słowy, Q’(s,a) spełnia równanie Bellmana dla MDP M’. Teraz możemy wyodrębnić optymalną politykę dla M’ za pomocą równania
![]()
Funkcja Φ(s) jest często nazywana potencjałem, przez analogię do potencjału elektrycznego (napięcia), który powoduje powstawanie pól elektrycznych. Termin γΦ(s’)-Φ(s) funkcjonuje jako gradient potencjału. Tak więc, jeśli Φ(s) ma większą wartość w stanach o większej użyteczności, dodanie γ Φ(s’)-Φ(s) do nagrody skutkuje prowadzeniem agenta „pod górę” użyteczności. Na pierwszy rzut oka może wydawać się dość sprzeczne z intuicją, że możemy w ten sposób modyfikować nagrodę bez zmiany optymalnej polityki. Dobrze, jeśli pamiętamy, że wszystkie zasady są optymalne, a funkcja nagrody jest wszędzie zerowa. Oznacza to, zgodnie z twierdzeniem o kształtowaniu, że wszystkie taktyki są optymalne dla dowolnej nagrody opartej na potencjale postaci R(s,a,s’) = γΦ(s’)- Φ(s). Intuicyjnie dzieje się tak, ponieważ przy takiej nagrodzie nie ma znaczenia, w którą stronę przechodzi agent z A do B. (Najłatwiej to zobaczyć, gdy γ=1: wzdłuż dowolnej ścieżki suma nagród spada do Φ(B)-Φ(A), więc wszystkie ścieżki są równie dobre.) Zatem dodanie nagrody opartej na potencjale do jakiejkolwiek innej nagrody nie powinno zmieniać optymalnej polityki. Elastyczność zapewniana przez twierdzenie o kształtowaniu oznacza, że możemy faktycznie pomóc agentowi, sprawiając, że natychmiastowa nagroda bardziej bezpośrednio odzwierciedla to, co agent powinien zrobić. W rzeczywistości, jeśli ustawimy Φ(s)=U(s), to zachłanna polityka G w odniesieniu do zmodyfikowanej nagrody R’ jest również optymalną polityką:
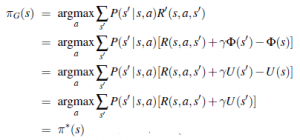
Oczywiście, aby ustawić Φ(s)=U(s), musielibyśmy znać U(s); więc nie ma darmowego lunchu, ale nadal istnieje znaczna wartość w zdefiniowaniu funkcji nagrody, która jest pomocna w możliwym zakresie. To jest dokładnie to, co robią trenerzy zwierząt, kiedy zapewniają zwierzęciu mały smakołyk na każdym etapie sekwencji docelowej