Załóżmy, że agent znajduje się w środowisku 4x 3 pokazanym na rysunku (a).
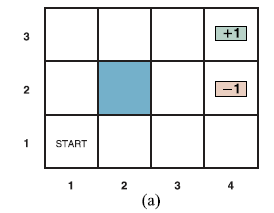
Począwszy od stanu początkowego, musi wybrać akcję w każdym kroku czasowym. Interakcja z otoczeniem kończy się, gdy agent osiągnie jeden ze stanów docelowych, oznaczonych jako +1 lub –1. Podobnie jak w przypadku problemów z wyszukiwaniem, działania dostępne dla agenta w każdym stanie są podane jako ACTIONS, czasami skracane do A(s); w środowisku 4 3 działania w każdym stanie to Góra, Dół, Lewo i Prawo. Na razie zakładamy, że środowisko jest w pełni obserwowalne, dzięki czemu agent zawsze wie, gdzie się znajduje. Gdyby środowisko było deterministyczne, rozwiązanie byłoby proste: [W górę, W górę, W prawo, W prawo, W prawo]. Niestety, środowisko nie zawsze przyjmie takie rozwiązanie, ponieważ działania są zawodne. Konkretny model ruchu stochastycznego, który przyjmujemy, ilustruje rysunek (b).
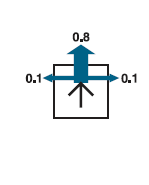
Każde działanie osiąga zamierzony efekt z prawdopodobieństwem 0,8, ale przez resztę czasu działanie przesuwa agenta pod kątem prostym do zamierzonego kierunku. Co więcej, jeśli agent wpadnie na ścianę, pozostanie na tym samym kwadracie. Na przykład od pola początkowego (1,1) akcja Up przesuwa agenta do (1,2) z prawdopodobieństwem 0,8, ale z prawdopodobieństwem 0,1 przesuwa się w prawo do (2,1), a z prawdopodobieństwem 0,1 porusza się w lewo, uderza w ścianę i pozostaje w (1,1). W takim środowisku sekwencja [Up;Up; Prawidłowy; Prawidłowy; Po prawej] wznosi się wokół bariery i osiąga stan docelowy na poziomie (4,3) z prawdopodobieństwem 0,85=0:32768. Istnieje również niewielka szansa na przypadkowe osiągnięcie celu, postępując w drugą stronę z prawdopodobieństwem 0,14 0:8, co daje całkowitą sumę 0,32776. Podobnie jak w rozdziale 3, model przejścia (lub po prostu „model”, gdy znaczenie jest jasne) opisuje wynik każdego działania w każdym stanie. Tutaj wynik jest stochastyczny, więc zapisujemy P(s’| s,a) dla prawdopodobieństwa osiągnięcia stanu s’, jeśli akcja a jest wykonana w stanie s. (Niektórzy autorzy piszą T(s,a,s’) dla modelu przejścia.) Założymy, że przejścia są markowskie: prawdopodobieństwo osiągnięcia s’ z s zależy tylko od s, a nie od historii wcześniejszych stanów. Aby zakończyć definicję środowiska zadań, musimy określić funkcję użytkową dla agenta. Ponieważ problem decyzyjny jest sekwencyjny, funkcja użyteczności będzie zależeć od sekwencji stanów i działań – historii środowiska – a nie od pojedynczego stanu. W dalszej części tej sekcji zbadamy naturę funkcji użyteczności na historiach; na razie po prostu zakładamy, że za każde przejście od s do s’ poprzez akcję a agent otrzymuje nagrodę R(s,a,s’). Nagrody mogą być pozytywne lub negatywne, ale są ograniczone przez ±Rmax.
W naszym konkretnym przykładzie nagroda wynosi -0,04 dla wszystkich przejść z wyjątkiem tych, które wchodzą w stany końcowe (które mają nagrody +1 i -1). Użyteczność historii środowiska to tylko (na razie) suma otrzymanych nagród. Na przykład, jeśli agent osiągnie stan +1 po 10 krokach, jego całkowita użyteczność wyniesie (9 x -0,04)+1=0,64. Negatywna nagroda -0,04 daje agentowi motywację do szybkiego dotarcia do (4,3), więc nasze środowisko jest stochastycznym uogólnieniem problemów wyszukiwania z rozdziału 3. Innym sposobem powiedzenia tego jest to, że agent nie lubi żyć w tym środowiska i dlatego chce jak najszybciej wyjechać. Podsumowując: sekwencyjny problem decyzyjny dla w pełni obserwowalnego, stochastycznego środowiska z modelem przejścia Markowa i addytywnymi nagrodami nazywa się procesem decyzyjnym Markowa lub MDP i składa się ze zbioru stanów (ze stanem początkowym s0); zestaw działań w każdym stanie; model przejściowy P(s’ | s,a); oraz funkcję nagrody R(s,a,s’). Metody rozwiązywania MDP zwykle obejmują programowanie dynamiczne: uproszczenie problemu poprzez rekurencyjne dzielenie go na mniejsze części i zapamiętywanie optymalnych rozwiązań dla części. Kolejne pytanie brzmi: jak wygląda rozwiązanie problemu? Żadna ustalona sekwencja działań nie może rozwiązać problemu, ponieważ agent może znaleźć się w stanie innym niż cel. Dlatego rozwiązanie musi określać, co agent powinien zrobić dla dowolnego stanu, do którego agent może dotrzeć. Tego rodzaju rozwiązanie polityczne nazywa się polityką. Tradycyjnie oznacza się politykę przez π , a π(s) jest działaniem zalecanym przez politykę dla stanu s. Bez względu na wynik działania, wynikowy stan znajdzie się w polisie, a agent będzie wiedział, co dalej. Za każdym razem, gdy dana polityka jest realizowana od stanu początkowego, stochastyczny charakter środowiska może prowadzić do innej historii środowiska. Jakość polityki jest zatem mierzona oczekiwaną użytecznością możliwych historii środowiskowych generowanych przez tę politykę. Polityka optymalna to polityka, która zapewnia najwyższą oczekiwaną użyteczność. Używamy π* do określenia optymalnej polityki. Biorąc pod uwagę π*, agent decyduje, co zrobić, sprawdzając swoją bieżącą percepcję, która informuje go o bieżącym stanie s, a następnie wykonuje akcję π*(s). Strategia jawnie reprezentuje funkcję agenta, a zatem jest opisem prostego agenta odruchowego, obliczonym na podstawie informacji używanych dla agenta opartego na narzędziach. Optymalne polityki dla świata z rysunku pierwszego pokazano na rysunku (a).
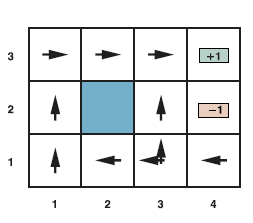
Istnieją dwie zasady, ponieważ agentowi jest dokładnie obojętne, czy pójdzie w lewo, czy w górę z (3,1): przejście w lewo jest bezpieczniejsze, ale dłuższe, podczas gdy wchodzenie w górę jest szybsze, ale ryzykuje przypadkowe wpadnięcie w (4,2). Ogólnie rzecz biorąc, często istnieje wiele optymalnych polityk.
Bilans ryzyka i nagrody zmienia się w zależności od wartości r=R(s,a,s’) dla przejść między stanami nieterminalnymi. Zasady przedstawione na rysunku (a) są optymalne dla -0,0850 < r < -0,0273. Rysunek (b) pokazuje optymalne polityki dla czterech innych zakresów r.
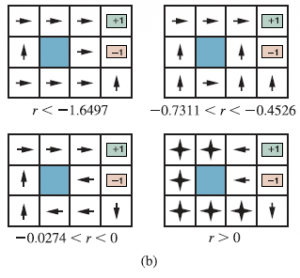
Gdy r < -1,6497, życie jest tak bolesne, że agent kieruje się prosto do najbliższego wyjścia, nawet jeśli wyjście jest warte –1. Gdy -0,7311 < r < -0,4526, życie jest dość nieprzyjemne; agent wybiera najkrótszą drogę do stanu +1 z (2,1), (3,1) i (3,2), ale z (4,1) koszt osiągnięcia +1 jest tak wysoki, że agent woli zanurkować prosto w -1. Kiedy życie jest tylko trochę posępne (-0,0274 < r < 0), optymalna polityka nie wiąże się z żadnym ryzykiem. W (4,1) i (3,2) agent odchodzi bezpośrednio od stanu –1, aby nie wpaść przez przypadek, mimo że oznacza to kilkakrotne uderzenie głową o ścianę. Wreszcie, jeśli r > 0, to życie jest pozytywnie przyjemne i agent unika obu wyjść. Dopóki działania w (4,1), (3,2) i (3,3) są takie, jak pokazano, każda polityka jest optymalna, a agent otrzymuje nieskończoną całkowitą nagrodę, ponieważ nigdy nie wchodzi w stan terminalny. Okazuje się, że w sumie istnieje dziewięć optymalnych taktyk dla różnych zakresów r; Ćwiczenie 16.THRC prosi cię o ich odnalezienie. Wprowadzenie niepewności przybliża MDP do świata rzeczywistego niż problemy wyszukiwania deterministycznego. Z tego powodu MDP badano w kilku dziedzinach, w tym w sztucznej inteligencji, badaniach operacyjnych, ekonomii i teorii sterowania.