Przejdźmy teraz do drugiego z wyżej wymienionych przypadków: maszyny, która ma pomagać człowiekowi, ale nie jest pewna, czego człowiek chce. Pełne rozpatrzenie tej sprawy należy odroczyć do rozdziału 17, w którym omawiamy decyzje dotyczące więcej niż jednego agenta. Tutaj zadajemy jedno proste pytanie: w jakich okolicznościach taka maszyna będzie podporządkowywać się człowiekowi. Aby zbadać to pytanie, rozważmy bardzo prosty scenariusz, jak pokazano na rysunku
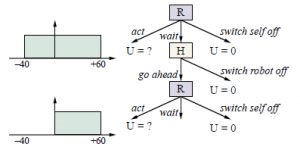
Robbie to robot programowy pracujący dla Harriet, zapracowanego człowieka, jako jej osobisty asystent. Harriet potrzebuje pokoju w hotelu na następne spotkanie biznesowe w Genewie. Robbie może teraz działać – powiedzmy, że może zarezerwować Harriet w bardzo drogim hotelu w pobliżu miejsca spotkania. Nie jest pewien, jak bardzo Harriet spodoba się hotel i jego cena; powiedzmy, że ma jednolite prawdopodobieństwo jego wartości netto dla Harriet między -40 a +60, ze średnią +10. Mógł też „wyłączyć się” – mniej melodramatycznie, całkowicie wyłączyć się z procesu rezerwacji hotelu – który definiujemy (bez utraty ogólności), że ma wartość 0 dla Harriet. Gdyby to były jego dwie możliwości, poszedłby dalej i zarezerwował hotel, ponosząc znaczne ryzyko, że unieszczęśliwi Harriet. (Gdyby zakres wynosił od -60 do +40, przy średniej -10, zamiast tego wyłączyłby się.) Damy Robbie jednak trzeci wybór: wyjaśnij jego plan, poczekaj i pozwól Harriet go wyłączyć. Harriet może go wyłączyć lub pozwolić mu zarezerwować hotel. Ktoś mógłby zapytać, co mogłoby z tego wyniknąć, skoro sam mógł dokonać obu tych wyborów? Chodzi o to, że wybór Harriet – wyłączyć Robbiego lub pozwolić mu iść dalej – zapewnia:
Robbie z informacją o preferencjach Harriet. Na razie założymy, że Harriet jest racjonalna, więc jeśli Harriet pozwoli Robbiemu iść dalej, oznacza to, że wartość dla Harriet jest dodatnia. Teraz, jak pokazano na rysunku 15.11, przekonanie Robbiego zmienia się: jest jednolite od 0 do +60, ze średnią +30. Jeśli więc ocenimy początkowe wybory Robbiego z jego punktu widzenia:
- Działając teraz i rezerwując hotel ma oczekiwaną wartość +10.
- Wyłączenie się ma wartość 0.
- Czekanie i pozwolenie Harriet na wyłączenie go prowadzi do dwóch możliwych rezultatów:
(a) Istnieje 40% szans, w oparciu o niepewność Robbiego co do preferencji Harriet, że znienawidzi plan i wyłączy Robbiego, z wartością 0.
(b) Istnieje 60% szans, że Harriet spodoba się plan i pozwoli Robbiemu kontynuować, z oczekiwaną wartością +30.
Zatem czekanie ma wartość oczekiwaną (0:4 0)+(0:6 30)= +18, co jest lepsze niż +10, których Robbie oczekuje, jeśli zadziała teraz.
W rezultacie Robbie ma pozytywną motywację, by poddać się Harriet – to znaczy pozwolić sobie na wyłączenie. Ta zachęta pochodzi bezpośrednio z niepewności Robbiego co do preferencji Harriet. Robbie zdaje sobie sprawę, że istnieje szansa (w tym przykładzie 40%), że może zrobić coś, co sprawi, że Harriet będzie nieszczęśliwa, w takim przypadku wyłączenie byłoby lepsze niż kontynuowanie. Gdyby Robbie był już pewien preferencji Harriet, po prostu podjąłby decyzję (lub wyłączyłby się); konsultując się z Harriet, nie dałoby się absolutnie nic zyskać, ponieważ zgodnie z przekonaniami Robbiego, Robbie może już przewidzieć, co ona zdecyduje. W rzeczywistości możliwe jest udowodnienie tego samego wyniku w ogólnym przypadku: dopóki Robbie nie jest całkowicie pewien, że ma zamiar zrobić to, co zrobiłaby sama Harriet, lepiej pozwolić jej się wyłączyć. Intuicyjnie jej decyzja dostarcza Robbiemu informacji, a oczekiwana wartość informacji jest zawsze nieujemna. I odwrotnie, jeśli Robbie jest pewien decyzji Harriet, jej decyzja nie dostarcza nowych informacji, a więc Robbie nie ma motywacji, by pozwolić jej na podjęcie decyzji. Formalnie niech P(u) będzie wcześniejszą gęstością prawdopodobieństwa Robbiego nad użytecznością Harriet dla proponowanego działania a. Wtedy wartość kontynuacji z a jest
![]()
(Niedługo zobaczymy, dlaczego całka jest podzielona w ten sposób.) Z drugiej strony, wartość działania d, odnosząc się do Harriet, składa się z dwóch części: jeśli u > 0, to Harriet pozwala Robbiemu kontynuować, więc wartość to u, ale jeśli u < 0, Harriet wyłącza Robbiego, więc wartość wynosi 0:
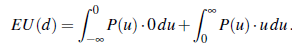
Porównując wyrażenia na EU(a) i EU(d), od razu widzimy, że
![]()
ponieważ wyrażenie dla EU(d) ma wyzerowany obszar użyteczności ujemnej. Te dwa wybory mają jednakową wartość tylko wtedy, gdy obszar ujemny ma zerowe prawdopodobieństwo — to znaczy, gdy Robbie jest już pewien, że Harriet podoba się proponowane działanie. Istnieje kilka oczywistych opracowań modelu, które warto natychmiast zbadać. Pierwszym opracowaniem jest nałożenie kosztów na czas Harriet. W takim przypadku Robbie jest mniej skłonny do zawracania sobie głowy Harriet, jeśli ryzyko pogorszenia sytuacji jest niewielkie. Tak powinno być. A jeśli Harriet jest naprawdę zrzędliwa, że ktoś jej przerywa, nie powinna być zbyt zdziwiona, jeśli Robbie od czasu do czasu robi rzeczy, których nie lubi. Drugie opracowanie uwzględnia pewne prawdopodobieństwo błędu ludzkiego – to znaczy, że Harriet może czasami wyłączyć Robbiego, nawet jeśli jego proponowane działanie jest rozsądne, a czasami może pozwolić Robbiemu kontynuować, nawet jeśli jego proponowane działanie jest niepożądane. Łatwo jest umieścić to prawdopodobieństwo błędu w modelu. Jak można się spodziewać, rozwiązanie pokazuje, że Robbie jest mniej skłonny do podporządkowywania się irracjonalnej Harriet, która czasami działa wbrew jej własnym interesom. Im bardziej przypadkowo się zachowuje, tym bardziej Robbie musi być niepewny co do jej preferencji, zanim się jej podporządkowuje. Znowu tak powinno być: na przykład, jeśli Robbie jest samojezdnym samochodem, a Harriet jest jego niegrzecznym dwuletnim pasażerem, Robbie nie powinien pozwolić Harriet wyłączyć go na środku autostrady.