Wyprowadzenie ogólnego wzoru matematycznego na wartość informacji jest proste. Zakładamy, że można uzyskać dokładne dowody o wartości jakiejś zmiennej losowej Ej (czyli uczymy się Ej = ej), więc użyto wyrażenia wartość doskonałej informacji (VPI) W początkowym stanie informacyjnym agenta wartość aktualna najlepsza akcja α to, z równania,
![]()
a wartość nowego najlepszego działania (po uzyskaniu nowego dowodu Ej = ej) będzie
![]()
Ale Ej jest zmienną losową, której wartość jest obecnie nieznana, więc aby określić wartość odkrycia Ej, musimy uśrednić wszystkie możliwe wartości ej, które możemy odkryć dla Ej, korzystając z naszych obecnych przekonań na temat jej wartości:
![]()
Aby uzyskać intuicję dla tego wzoru, rozważ prosty przypadek, w którym do wyboru są tylko dwie akcje, a1 i a2. Ich obecne oczekiwane media to U1 i U2. Informacja Ej = ej da pewne nowe oczekiwane użyteczności U0 1 i U0 2 dla działań, ale zanim uzyskamy Ej, będziemy mieć pewne rozkłady prawdopodobieństwa nad możliwymi wartościami U’1 i U’2 (które zakładamy, że są niezależne). Załóżmy, że a1 i a2 reprezentują dwie różne trasy przez łańcuch górski zimą: a1 to ładna, prosta autostrada przez tunel, a a2 to kręta droga gruntowa biegnąca przez szczyt. Biorąc pod uwagę te informacje, a1 jest wyraźnie preferowane, ponieważ jest całkiem możliwe, że a2 jest blokowane przez śnieg, podczas gdy jest mało prawdopodobne, aby cokolwiek blokowało a1. U1 jest więc wyraźnie wyższy niż U2. Możliwe jest uzyskanie raportów satelitarnych Ej o aktualnym stanie każdej drogi, które dałyby nowe oczekiwania, U’1 i U’2, dla obu skrzyżowań. Rozkłady tych oczekiwań przedstawiono na rysunku (a).
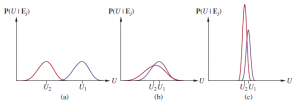
Oczywiście w tym przypadku nie warto ponosić kosztów pozyskiwania raportów satelitarnych, ponieważ jest mało prawdopodobne, aby informacje z nich czerpane zmieniły plan. Bez zmian informacja nie ma wartości. Załóżmy teraz, że wybieramy między dwiema różnymi krętymi drogami gruntowymi o nieco różnych długościach i przewozimy ciężko rannego pasażera. Wtedy, nawet gdy U1 i U2 są dość zbliżone, rozkłady U’1 i U’2 są bardzo szerokie. Istnieje duże prawdopodobieństwo, że druga trasa okaże się pusta, podczas gdy pierwsza będzie zablokowana, a w tym przypadku różnica w mediach będzie bardzo duża. Formuła VPI wskazuje, że warto byłoby uzyskać raporty satelitarne. Taka sytuacja jest pokazana na rysunku (b). Na koniec załóżmy, że wybieramy między dwiema drogami gruntowymi latem, kiedy zablokowanie przez śnieg jest mało prawdopodobne. W tym przypadku raporty satelitarne mogą wskazywać, że jedna trasa jest bardziej malownicza niż druga z powodu kwitnących łąk alpejskich lub być może bardziej wilgotna z powodu niedawnego deszczu. Jest zatem całkiem prawdopodobne, że gdybyśmy mieli te informacje, zmienilibyśmy nasz plan. W tym przypadku jednak różnica w wartości między tymi dwiema trasami prawdopodobnie nadal będzie bardzo mała, więc nie będziemy zawracać sobie głowy otrzymywaniem raportów. Ta sytuacja jest pokazana na rysunku (c). Podsumowując, informacja ma wartość do tego stopnia, że prawdopodobnie spowoduje zmianę planu, a J do tego stopnia, że nowy plan będzie znacznie lepszy niż stary.