Załóżmy, że teren lotniska S1 kosztuje mniej, generuje mniej hałasu i jest bezpieczniejszy niż teren S2. Nie zawahałoby się odrzucić S2. Mówimy wtedy, że istnieje ścisła dominacja S1 nad S2. Ogólnie rzecz biorąc, jeśli opcja ma niższą wartość we wszystkich atrybutach niż jakaś inna opcja, nie trzeba jej dalej rozważać. Ścisła dominacja jest często bardzo przydatna w zawężaniu pola wyboru do prawdziwych rywali, chociaż rzadko daje unikalny wybór. Rysunek (a) przedstawia schematyczny diagram dla przypadku z dwoma atrybutami.
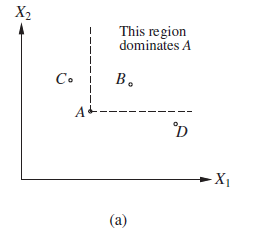
To dobrze w przypadku deterministycznym, w którym wartości atrybutów są na pewno znane. A co z ogólnym przypadkiem, w którym wyniki są niepewne? Można skonstruować bezpośredni analog ścisłej dominacji, w której pomimo niepewności wszystkie możliwe konkretne wyniki dla S1 ściśle dominują nad wszystkimi możliwymi wynikami dla S2. (Patrz rysunek (b))
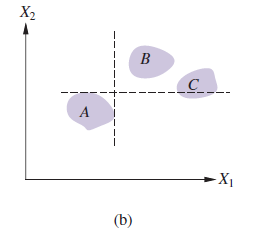
Oczywiście będzie to prawdopodobnie zdarzać się nawet rzadziej niż w przypadku deterministycznym. Na szczęście istnieje bardziej przydatne uogólnienie zwane dominacją stochastyczną, która występuje bardzo często w rzeczywistych problemach. Dominację stochastyczną najłatwiej zrozumieć w kontekście pojedynczego atrybutu. Załóżmy, że wierzymy, że koszt umieszczenia lotniska w S1 jest równomiernie rozłożony między 2,8 miliarda a 4,8 miliarda USD, a koszt w S2 jest równomiernie rozłożony między 3 miliardami a 5,2 miliarda USD. Zdefiniuj atrybut Oszczędność jako koszt ujemny. Rysunek (a) pokazuje rozkłady oszczędności miejsc S1 i S2. Następnie, mając tylko informację, że oszczędniejszy wybór jest lepszy (wszystkie inne czynniki są równe), możemy powiedzieć, że S1 stochastycznie dominuje nad S2 (tj. S2 można odrzucić). Należy zauważyć, że nie wynika to z porównania oczekiwanych kosztów. Na przykład, gdybyśmy wiedzieli, że koszt S1 wynosi dokładnie 3,8 miliarda dolarów, nie bylibyśmy w stanie podjąć decyzji bez dodatkowych informacji o użyteczności pieniędzy. (Może wydawać się dziwne, że więcej informacji na temat kosztu S1 może sprawić, że agent będzie mniej zdolny do podjęcia decyzji. Paradoks rozwiązuje się, zauważając, że przy braku dokładnych informacji o kosztach decyzja jest łatwiejsza do podjęcia, ale jest bardziej prawdopodobne, że będzie błędna .) Dokładny związek między rozkładami atrybutów potrzebnymi do ustalenia dominacji stochastycznej najlepiej widać, badając rozkłady skumulowane, pokazane na rysunku (b). Jeśli rozkład skumulowany dla S1 jest zawsze na prawo od rozkładu skumulowanego dla S2, to, mówiąc stochastycznie, S1 jest tańszy niż S2. Formalnie, jeśli dwa działania A1 i A2 prowadzą do rozkładów prawdopodobieństwa p1(x) i p2(x) na atrybucie X, to A1 stochastycznie dominuje A2 na X, jeśli
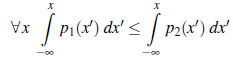
Znaczenie tej definicji dla wyboru optymalnych decyzji wynika z następującej własności: jeśli A1 stochastycznie dominuje nad A2, to dla dowolnej monotonicznie nie malejącej funkcji użyteczności U(x), oczekiwana użyteczność A1 jest co najmniej tak wysoka, jak oczekiwana użyteczność A2 . Aby zobaczyć, dlaczego tak jest, rozważmy dwie oczekiwane narzędzia, ∫p1(x)U(x)dx i ∫p2(x)U(x)dx. Początkowo nie jest oczywiste, dlaczego pierwsza całka jest większa niż druga, biorąc pod uwagę, że warunek dominacji stochastycznej ma całkę p1, która jest mniejsza niż całka p2.
Jednak zamiast myśleć o całce przez x, pomyśl o całce przez y, skumulowanym prawdopodobieństwie, jak pokazano na rysunku (b).
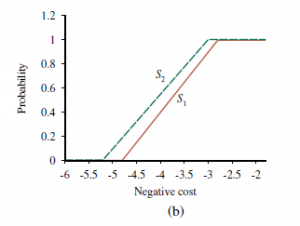
Dla dowolnej wartości y, odpowiadająca jej wartość x (a zatem U(x)) jest większa dla S1 niż dla S2; więc jeśli scałkujemy większą ilość w całym zakresie y, otrzymamy większy wynik. Formalnie jest to po prostu podstawienie y=P1(x) w całce za wartość oczekiwaną S1 i y=P2(x) w całce dla S2. Z tego podstawienia, mamy dy= d/dx (P1(x))dx=p1(x)dx dla S1 i dy=p2(x)dx dla S2, stąd
![]()
Ta nierówność pozwala nam preferować A1 do A2 w problemie jednoatrybutowym. Mówiąc bardziej ogólnie, jeśli działanie jest stochastycznie zdominowane przez inne działanie dotyczące wszystkich atrybutów w problemie wieloatrybutowym, można je odrzucić. Warunek dominacji stochastycznej może wydawać się raczej techniczny i być może nie tak łatwy do oceny bez rozległych obliczeń prawdopodobieństwa. W rzeczywistości w wielu przypadkach można to bardzo łatwo rozstrzygnąć. Na przykład, czy wolisz paść głową na beton z 3 milimetrów czy 3 metrów? Zakładając, że wybrałeś 3 milimetry – dobry wybór! Dlaczego jest to koniecznie lepsza decyzja? Istnieje duża niepewność co do stopnia szkód, które poniesiesz w obu przypadkach; ale dla dowolnego poziomu obrażeń prawdopodobieństwo, że poniesiesz co najmniej ten poziom obrażeń, jest wyższe, gdy spadniesz z 3 metrów niż z 3 milimetrów. Innymi słowy, 3 milimetry stochastycznie dominują 3 metry w atrybucie Bezpieczeństwo. Ten rodzaj rozumowania jest dla ludzi drugą naturą; to tak oczywiste, że nawet o tym nie myślimy. Stochastyczna dominacja obfituje również w problem lotniska. Załóżmy na przykład, że koszt transportu budowlanego zależy od odległości do dostawcy. Sam koszt jest niepewny, ale im większa odległość, tym większy koszt. Jeśli S1 jest bliżej niż S2, to S1 zdominuje S2 pod względem oszczędności. Chociaż nie będziemy ich tutaj przedstawiać, istnieją algorytmy propagowania tego rodzaju informacji jakościowych wśród zmiennych niepewnych w jakościowych sieciach probabilistycznych, umożliwiające systemowi podejmowanie racjonalnych decyzji opartych na dominacji stochastycznej, bez użycia wartości liczbowych.