Racjonalnym sposobem wyboru najlepszego działania a* , jest maksymalizacja oczekiwanej użyteczności:
Jeśli poprawnie obliczyliśmy oczekiwaną użyteczność zgodnie z naszym modelem prawdopodobieństwa i jeśli model prawdopodobieństwa poprawnie odzwierciedla procesy stochastyczne, które generują wyniki, to średnio otrzymamy oczekiwaną użyteczność, jeśli cały proces zostanie powtórzony wiele razy . W rzeczywistości jednak nasz model zwykle nadmiernie upraszcza rzeczywistą sytuację, ponieważ albo nie wiemy wystarczająco dużo (np. przy podejmowaniu złożonej decyzji inwestycyjnej), albo dlatego, że obliczenie rzeczywistej oczekiwanej użyteczności jest zbyt trudne (np. podczas wykonywania ruchu w tryktraku, należy wziąć pod uwagę wszystkie możliwe przyszłe rzuty kośćmi). W takim przypadku naprawdę pracujemy z oszacowaniami 
rzeczywistej oczekiwanej użyteczności. Być może uprzejmie założymy, że szacunki są bezstronne — to znaczy, że oczekiwana wartość błędu 
wynosi zero. W takim przypadku nadal wydaje się rozsądne, aby wybrać akcję o najwyższej oszacowanej użyteczności i oczekiwać, że akcja zostanie przeciętnie otrzymana, gdy akcja jest wykonywana. Niestety rzeczywisty wynik będzie zwykle znacznie gorszy niż szacowaliśmy, mimo że szacunki były obiektywne! Aby zobaczyć dlaczego, rozważmy problem decyzyjny, w którym istnieje k wyborów, z których każdy ma prawdziwą oszacowaną użyteczność równą 0. Załóżmy, że błąd w każdym oszacowaniu użyteczności jest niezależny i ma jednostkowy rozkład normalny – to jest gaussowski ze średnią zerową a odchylenie standardowe 1, pokazane jako pogrubiona krzywa na rysunku . Teraz, kiedy faktycznie zaczniemy generować szacunki, niektóre błędy będą ujemne (pesymistyczne), a inne dodatnie (optymistyczne). Ponieważ wybieramy działanie o najwyższej ocenie użyteczności, faworyzujemy zbyt optymistyczne szacunki i to jest źródłem błędu. Łatwo jest obliczyć rozkład maksimum oszacowań k, a tym samym określić ilościowo zakres naszego rozczarowania. (To obliczenie jest szczególnym przypadkiem obliczania statystyki rzędów, rozkładu dowolnego określonego uszeregowanego elementu próbki.) Załóżmy, że każde oszacowanie Xi ma funkcję gęstości prawdopodobieństwa f(x) i skumulowany rozkład F(x). Teraz niech X będzie największym oszacowaniem, tj. max{X1,…,Xk}. Wtedy skumulowany rozkład dla X* to
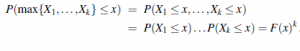
Funkcja gęstości prawdopodobieństwa jest pochodną funkcji rozkładu skumulowanego, więc gęstość dla X* , maksimum k oszacowań, wynosi
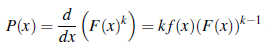
Te gęstości są pokazane dla różnych wartości k na rysunku 15.3 dla przypadku, w którym f(x) jest jednostką normalną.
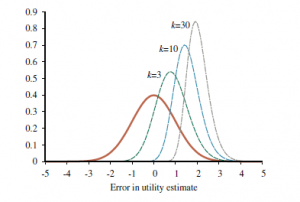
Dla k=3 gęstość dla X ma średnią około 0,85, więc średnie rozczarowanie wyniesie około 85% odchylenia standardowego w szacunkach użyteczności. Przy większej liczbie wyborów, bardziej prawdopodobne jest pojawienie się skrajnie optymistycznych szacunków: dla k=30 rozczarowanie będzie około dwukrotnością odchylenia standardowego w szacunkach. Ta tendencja do zbyt wysokiej szacowanej oczekiwanej użyteczności najlepszego wyboru nazywana jest przekleństwem optymalizatora . Dręczy nawet najbardziej doświadczonych analityków decyzyjnych i statystyków. Poważne przejawy obejmują przekonanie, że nowy, ekscytujący lek, który wyleczył 80% pacjentów w badaniu, wyleczy 80% pacjentów (został wybrany spośród tysięcy kandydatów na leki) lub że fundusz powierniczy reklamowany jako przynoszący ponadprzeciętne zyski nadal je mieć (został wybrany do wyświetlenia w reklamie spośród k=dziesiątek funduszy w całym portfelu firmy). Może się nawet zdarzyć, że to, co wydaje się być najlepszym wyborem, może nie być najlepszym wyborem, jeśli rozbieżność w ocenie użyteczności jest duża: lek, który wyleczył 9 na 10 pacjentów i został wybrany spośród tysięcy wypróbowanych, jest prawdopodobnie gorszy niż ten, który wyleczył 800 z 1000. Klątwa optymalizatora pojawia się wszędzie z powodu wszechobecności procesów selekcji maksymalizujących użyteczność, więc przyjmowanie oszacowań użyteczności według wartości nominalnej jest złym pomysłem. Możemy uniknąć klątwy dzięki podejściu bayesowskiemu, które wykorzystuje jawny model prawdopodobieństwa 
błędu w oszacowaniach użyteczności. Biorąc pod uwagę ten model i wcześniejszy opis tego, czego możemy racjonalnie oczekiwać od użyteczności, traktujemy oszacowanie użyteczności jako dowód i obliczamy rozkład a posteriori dla prawdziwej użyteczności, stosując regułę Bayesa.