Teoria użyteczności ma swoje korzenie w ekonomii, a ekonomia dostarcza jednego oczywistego kandydata na miarę użyteczności: pieniądza (a dokładniej, całkowitych aktywów netto agenta). Niemal powszechna wymienialność pieniądza na wszelkiego rodzaju dobra i usługi sugeruje, że pieniądz odgrywa znaczącą rolę w funkcjach użyteczności człowieka. Zwykle będzie tak, że agent woli więcej pieniędzy niż mniej, przy wszystkich innych rzeczach bez zmian. Mówimy, że agent wykazuje monotonną preferencję do większej ilości pieniędzy. Nie oznacza to, że pieniądz zachowuje się jak funkcja użyteczności, ponieważ nie mówi nic o preferencjach między loteriami z pieniędzmi. Załóżmy, że triumfowałeś nad innymi konkurentami w telewizyjnym teleturnieju. Gospodarz oferuje teraz wybór: albo możesz odebrać nagrodę w wysokości 1 000 000 $, albo postawić ją na jeden rzut monetą. Jeśli moneta wypadnie rewersem, nie otrzymasz nic, ale jeśli wypadnie reszek, otrzymasz 2 500 000 $. Jeśli jesteś jak większość ludzi, odrzuciłbyś hazard i zgarnął milion. Czy zachowujesz się irracjonalnie? Zakładając, że moneta jest uczciwa, oczekiwana wartość pieniężna (EMV) hazardu wynosi 1/2 (0 USD) + 1/2 (2 500 000 USD) = 1 250 000 USD, czyli więcej niż pierwotny 1 000 000 USD. Ale to niekoniecznie oznacza, że akceptacja hazardu jest lepszą decyzją. Załóżmy, że używamy Sn do oznaczenia stanu posiadania całkowitego bogactwa $n i że twoje obecne bogactwo wynosi k $. Oczekiwana użyteczność obu czynności przyjęcia i odrzucenia hazardu to:
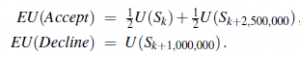
Aby określić, co zrobić, musimy przypisać narzędzia do stanów wynikowych. Użyteczność nie jest wprost proporcjonalna do wartości pieniężnej, ponieważ użyteczność pierwszego miliona jest bardzo wysoka (tak mówią), podczas gdy użyteczność dodatkowego miliona jest mniejsza. Załóżmy, że przypisujesz użyteczność 5 do swojego obecnego statusu finansowego (Sk), 9 do stanu Sk+2;500;000, a 8 do stanu Sk+1;000;000. Wtedy racjonalnym działaniem byłoby odrzucenie, ponieważ oczekiwana użyteczność akceptacji wynosi tylko 7 (mniej niż 8 dla odmowy). Z drugiej strony miliarder najprawdopodobniej miałby funkcję użyteczności, która jest lokalnie liniowa w zakresie kilku milionów więcej, a zatem zaakceptowałby ryzyko. W pionierskim badaniu rzeczywistych funkcji użyteczności Grayson (1960) odkrył, że użyteczność pieniądza była prawie dokładnie proporcjonalna do logarytmu wierzchowca. (Pomysł ten został po raz pierwszy zasugerowany przez Bernoulliego). Jedną szczególną krzywą użyteczności, dla pewnego pana Bearda, pokazano na rysunku (a).
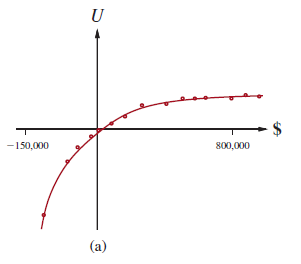
Dane uzyskane dla preferencji pana Bearda są zgodne z funkcją użyteczności
U(Sk+n) = -263:31+22:09log(n+150;000)
dla zakresu od n = – 150 000 $ do n = 800 000$. Nie powinniśmy zakładać, że jest to ostateczna funkcja użyteczności dla wartości pieniężnej, ale prawdopodobnie większość ludzi ma funkcję użyteczności wklęsłą dla pozytywnego bogactwa. Zadłużanie się jest złe, ale preferencje między różnymi poziomami zadłużenia mogą wskazywać na odwrócenie wklęsłości związanej z pozytywnym bogactwem. Na przykład ktoś, kto ma już 10 000 000 dolarów długu, może zgodzić się na grę na uczciwą monetę z zyskiem 10 000 000 w przypadku orła i stratą w wysokości 20 000 000 w przypadku reszka. Daje to krzywą w kształcie litery S pokazaną na rysunku (b).
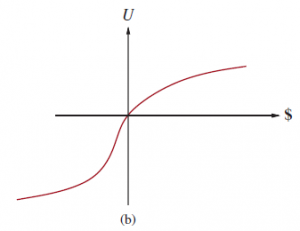
Jeśli ograniczymy naszą uwagę do dodatniej części krzywych, gdzie nachylenie maleje, to dla każdej loterii L użyteczność zmierzenia się z tą loterią jest mniejsza niż użyteczność otrzymania oczekiwanej wartości pieniężnej loterii jako pewna rzecz:
U(L) <U(SEMV(L)) :
Oznacza to, że agenci z krzywymi w tym kształcie mają awersję do ryzyka: wolą pewne rzeczy, których wypłata jest mniejsza niż oczekiwana wartość pieniężna zakładu. Z drugiej strony, w „rozpaczliwym” regionie na ogół ujemnym bogactwem na rysunku (b), zachowanie to poszukiwanie ryzyka. Wartość, jaką agent zaakceptuje zamiast loterii, nazywana jest ekwiwalentem pewności loterii. Badania wykazały, że większość ludzi zaakceptuje około 400 USD zamiast zakładu, który daje 1000 USD w połowie czasu, a 0 USD w drugiej połowie — to znaczy, że odpowiednik loterii wynosi 400 USD, podczas gdy EMV wynosi 500 USD. Różnica między EMV loterii a jej ekwiwalentem pewności nazywana jest składką ubezpieczeniową. Awersja do ryzyka jest podstawą branży ubezpieczeniowej, ponieważ oznacza to, że składki ubezpieczeniowe są dodatnie. Ludzie woleliby zapłacić niewielką składkę ubezpieczeniową, niż postawić cenę swojego domu na wypadek pożaru. Z punktu widzenia firmy ubezpieczeniowej cena domu jest bardzo niska w porównaniu z całkowitymi rezerwami firmy. Oznacza to, że krzywa użyteczności ubezpieczyciela jest w przybliżeniu liniowa na tak małym regionie, a hazard prawie nic nie kosztuje firmę. Zauważ, że w przypadku niewielkich zmian bogactwa w stosunku do obecnego bogactwa, prawie każda krzywa będzie w przybliżeniu liniowa. Mówi się, że agent, który ma krzywą liniową, jest neutralny pod względem ryzyka. W przypadku zakładów na małe sumy oczekujemy zatem neutralności ryzyka. W pewnym sensie uzasadnia to uproszczoną procedurę, która proponowała małe zakłady do oceny prawdopodobieństw i uzasadnienia aksjomatów prawdopodobieństwa