Opisano dwa algorytmy aproksymacji: ważenie wiarygodności i Monte Carlo łańcucha Markowa . Z tych dwóch ten pierwszy jest najłatwiej dostosowany do kontekstu DBN. Zobaczymy jednak, że przed pojawieniem się praktycznej metody wymagane jest kilka ulepszeń w stosunku do standardowego algorytmu ważenia wiarygodności. Przypomnijmy, że ważenie wiarygodności polega na próbkowaniu węzłów sieci w kolejności topologicznej, przy czym każda próbka jest ważona według prawdopodobieństwa, które odpowiada obserwowanym zmiennym dowodowym. Podobnie jak w przypadku dokładnych algorytmów, moglibyśmy zastosować ważenie prawdopodobieństwa bezpośrednio do rozwiniętego DBN, ale wiązałoby się to z tymi samymi problemami związanymi z rosnącymi wymaganiami czasowymi i przestrzennymi na aktualizację w miarę wzrostu sekwencji obserwacji. Problem polega na tym, że standardowy algorytm uruchamia po kolei każdą próbkę, przez całą sieć. Zamiast tego możemy po prostu uruchomić wszystkie N próbek razem przez DBN, po jednym wycinku na raz. Zmodyfikowany algorytm pasuje do ogólnego wzorca algorytmów filtrowania, z zestawem N próbek jako wiadomością do przodu. Pierwszą kluczową innowacją jest zatem wykorzystanie samych próbek jako przybliżonej reprezentacji obecnego rozkładu stanu. Spełnia to wymóg „stałego” czasu na aktualizację, chociaż stała zależy od liczby próbek wymaganych do utrzymania dokładnego przybliżenia. Nie ma również potrzeby rozwijania DBN, ponieważ musimy mieć w pamięci tylko bieżący i następny wycinek. Takie podejście nazywa się próbkowaniem według ważności sekwencyjnej lub SIS. W naszej dyskusji na temat ważenia prawdopodobieństwa w Rozdziale 13 zwróciliśmy uwagę, że dokładność algorytmu ucierpi, jeśli zmienne dowodowe znajdują się „poniżej” badanych zmiennych, ponieważ w takim przypadku próbki są generowane bez żadnego wpływu dowodów i prawie wszystkie mają bardzo niską wagę. Teraz, jeśli spojrzymy na typową strukturę DBN – powiedzmy, parasol DBN – widzimy, że rzeczywiście zmienne stanu wczesnego będą próbkowane bez korzyści z późniejszych dowodów. W rzeczywistości, przyglądając się uważniej, widzimy, że żadna ze zmiennych stanu nie ma żadnych zmiennych dowodowych wśród swoich przodków! Stąd, chociaż waga każdej próbki będzie zależeć od dowodów, rzeczywisty zestaw wygenerowanych próbek będzie całkowicie niezależny od dowodów. Na przykład, nawet jeśli szef codziennie przynosi parasol, proces pobierania próbek może nadal wywoływać halucynacje niekończących się słonecznych dni. W praktyce oznacza to, że ułamek próbek, które pozostają dość blisko rzeczywistej serii zdarzeń (a zatem mają nie pomijalne wagi) spada wykładniczo z t, długością sekwencji. Innymi słowy, aby utrzymać dany poziom dokładności, musimy zwiększać liczbę próbek wykładniczo z t. Biorąc pod uwagę, że algorytm filtrowania w czasie rzeczywistym może używać tylko ograniczonej liczby próbek, w praktyce błąd pojawia się po bardzo małej liczbie kroków aktualizacji. Rysunek
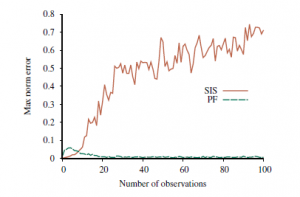
pokazuje ten efekt dla SIS zastosowany do problemu lokalizacji w świecie siatki: nawet przy 100 000 próbek aproksymacja SIS zawodzi całkowicie po około 20 krokach. Oczywiście potrzebujemy lepszego rozwiązania. Drugą kluczową innowacją jest skupienie zestawu próbek na obszarach o wysokim prawdopodobieństwie wystąpienia w przestrzeni stanów. Można to zrobić, wyrzucając próbki, które mają bardzo niską wagę, zgodnie z obserwacjami, podczas replikacji tych, które mają dużą wagę. W ten sposób populacja próbek pozostanie dość zbliżona do rzeczywistości. Jeśli myślimy o próbkach jako o zasobach do modelowania rozkładu a posteriori, sensowne jest użycie większej liczby próbek w obszarach przestrzeni stanów, w których a posteriori jest wyższa. Rodzina algorytmów zwana filtrowaniem cząstek jest przeznaczona właśnie do tego. (Inną wczesną nazwą było próbkowanie sekwencyjne z ponownym próbkowaniem, ale z jakiegoś powodu nie udało się to złapać.) Filtrowanie cząstek działa w następujący sposób: Najpierw generujemy populację N próbek z wcześniejszego rozkładu P(X0). Następnie cykl aktualizacji jest powtarzany dla każdego kroku czasowego:
- Każda próbka jest propagowana do przodu przez próbkowanie następnej wartości stanu xt+1 przy danej bieżącej wartości xt próbki, w oparciu o model przejścia P(Xt+1 | xt).
- Każda próbka jest ważona prawdopodobieństwem, które przypisuje nowemu dowodowi, P(et+1 | xt+1).
- Populacja jest ponownie próbkowana w celu wygenerowania nowej populacji N próbek. Każda nowa próbka jest wybierana z aktualnej populacji; prawdopodobieństwo wybrania określonej próbki jest proporcjonalne do jej wagi. Nowe próbki są nieważone.
Algorytm pokazano szczegółowo tu

a jego działanie dla parasola DBN pokazano na rysunku
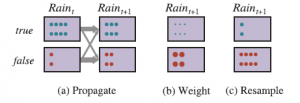
Możemy pokazać, że ten algorytm jest spójny — daje prawidłowe prawdopodobieństwa, ponieważ N dąży do nieskończoności — badając operacje w jednym cyklu aktualizacji. Zakładamy, że populacja próbek zaczyna się od poprawnej reprezentacji komunikatu przekazującego — to znaczy f1:t =P(Xt | e1:t) w czasie t. Zapisując N(xt | e1:t) dla liczby próbek zajmujących stan xt po przetworzeniu obserwacji e1:t, mamy zatem
![]()
dla dużego N. Teraz propagujemy każdą próbkę do przodu, próbkując zmienne stanu w czasie t +1, biorąc pod uwagę wartości dla próbki w t. Liczba próbek osiągających stan xt+1 z każdego xt jest prawdopodobieństwem przejścia pomnożonym przez populację xt ; stąd całkowita liczba próbek osiągających xt+1 wynosi
![]()
Teraz ważymy każdą próbkę według jej prawdopodobieństwa dla dowodu w t +1. Próbka w stanie xt+1 otrzymuje wagę P(et+1 | xt+1). Całkowita waga próbek w xt+1 po zobaczeniu et+1 wynosi zatem
![]()
Teraz czas na ponowne próbkowanie. Ponieważ każda próbka jest replikowana z prawdopodobieństwem proporcjonalnym do jej wagi, liczba próbek w stanie xt+1 po resamplingu jest proporcjonalna do całkowitej wagi w xt+1 przed resamplingiem:
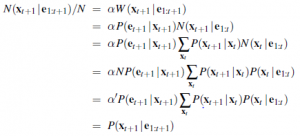
Dlatego populacja próbek po jednym cyklu aktualizacji prawidłowo reprezentuje komunikat do przodu w czasie t+1. Filtrowanie cząstek jest zatem spójne, ale czy jest skuteczne? W wielu praktycznych przypadkach wydaje się, że odpowiedź brzmi tak: filtrowanie cząstek wydaje się utrzymywać dobre przybliżenie do prawdziwego a posteriori przy użyciu stałej liczby próbek. Rysunek pokazuje, że filtrowanie cząstek dobrze radzi sobie z problemem lokalizacji w świecie siatki przy zaledwie tysiącu próbek.
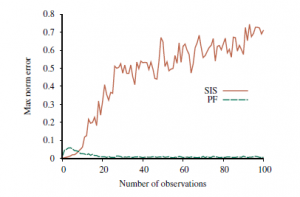
Działa również w rzeczywistych problemach: algorytm obsługuje tysiące zastosowań w nauce i inżynierii. (Niektóre odniesienia podano na końcu rozdziału.) Obsługuje kombinacje zmiennych dyskretnych i ciągłych, a także modele nieliniowe i niegaussowskie dla zmiennych ciągłych. Przy pewnych założeniach – w szczególności, że prawdopodobieństwa w modelach przejścia i czujników są ograniczone od 0 i 1 – można również wykazać, że aproksymacja utrzymuje błąd ograniczony z dużym prawdopodobieństwem, jak sugeruje rysunek. Algorytm filtrowania cząstek ma jednak słabości. Zobaczmy, jak radzi sobie w świecie próżni z dodanym brudem. Przypomnijmy, że zwiększa to rozmiar przestrzeni stanów o współczynnik 242, czyniąc dokładne wnioskowanie HMM niewykonalne. Chcemy, aby robot wędrował po okolicy i budował mapę lokalizacji brudu. (Jest to prosty przykład jednoczesnej lokalizacji i mapowania lub SLAM, który omówimy bardziej szczegółowo w rozdziale 26.) Niech Dirti;t oznacza, że kwadrat i jest brudny w czasie t i niech DirtSensort będzie prawdziwe wtedy i tylko wtedy, gdy robot wykryje brud w czasie t. Założymy, że w dowolnym kwadracie brud pozostaje z prawdopodobieństwem p, podczas gdy czysty kwadrat staje się brudny z prawdopodobieństwem 1p (co oznacza, że każdy kwadrat jest brudny średnio przez połowę czasu). Robot posiada czujnik zabrudzenia dla swojej aktualnej lokalizacji; czujnik jest dokładny z prawdopodobieństwem 0,9. Rysunek przedstawia DBN.
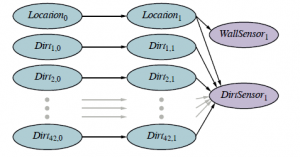
Dla uproszczenia zaczniemy od założenia, że robot ma doskonały czujnik lokalizacji, a nie zaszumiony czujnik ścienny. Działanie algorytmu pokazano na rysunku (a), gdzie jego oszacowania dla zabrudzenia są porównywane z wynikami dokładnego wnioskowania.
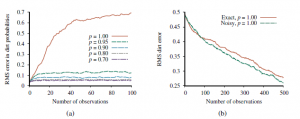
(Niedługo zobaczymy, jak dokładne jest możliwe wnioskowanie.) Przy niskich wartościach trwałości brudu p błąd pozostaje mały – ale nie jest to wielkie osiągnięcie, ponieważ dla każdego kwadratu prawdziwy a posteriori dla brudu jest bliski 0,5, jeśli robot nie odwiedził ostatnio tego placu. Przy wyższych wartościach p brud pozostaje dłużej, więc odwiedzenie kwadratu daje więcej przydatnych informacji, które są ważne przez dłuższy czas. Być może zaskakujące jest to, że filtrowanie cząstek działa gorzej dla wyższych wartości p. Zawodzi całkowicie, gdy p=1, chociaż wydaje się to najłatwiejszym przypadkiem: brud pojawia się w czasie 0 i zostaje na zawsze, więc po kilku wycieczkach po świecie robot powinien mieć prawie idealną mapę brudu. Dlaczego filtrowanie cząstek w tym przypadku nie działa?
Okazuje się, że teoretyczny warunek wymagający, aby „prawdopodobieństwa w modelach przejść i czujników były ściśle większe od 0 i mniejsze od 1” jest czymś więcej niż tylko matematyczną pedantyzmem. Najpierw każda cząstka zawiera 42 domysły z P(X0) o tym, które kwadraty są brudne, a które nie. Następnie stan każdej cząstki jest rzutowany do przodu w czasie zgodnie z modelem przejściowym. Niestety, model przejściowy dla brudu deterministycznego jest deterministyczny: brud pozostaje dokładnie tam, gdzie jest. Tak więc początkowe domysły w każdej cząstce nigdy nie są aktualizowane przez dowody. Szansa, że wszystkie wstępne domysły są poprawne, wynosi 2-42 lub około 2×10-13, więc jest znikome prawdopodobieństwo, że tysiąc cząstek (lub nawet milion cząstek) będzie zawierało jedną z poprawną mapą brudu. Zazwyczaj najlepsza cząstka z tysiąca otrzyma około 32 dobrze, a 10 źle, i zwykle będzie tylko jedna taka cząstka, a może garść. Jedna z tych najlepszych cząstek zdominuje całkowite prawdopodobieństwo w miarę upływu czasu i załamie się różnorodność populacji cząstek. Następnie, ponieważ wszystkie cząstki zgadzają się na jednej, niepoprawnej mapie, algorytm nabiera przekonania, że mapa jest poprawna i nigdy nie zmienia zdania. Na szczęście problem jednoczesnej lokalizacji i mapowania ma szczególną strukturę: uzależnione od kolejności lokalizacji robotów, stany zabrudzenia poszczególnych kwadratów są niezależne. Dokładniej,
![]()
Oznacza to, że warto zastosować sztuczkę statystyczną o nazwie Rao-Blackwellization, która opiera się na prostym założeniu, że dokładne wnioskowanie jest zawsze dokładniejsze niż próbkowanie, nawet jeśli dotyczy tylko podzbioru zmiennych. (Patrz Ćwiczenie 14.RAOB.) W przypadku problemu SLAM uruchamiamy filtrowanie cząstek w lokalizacji robota, a następnie dla każdej cząstki wykonujemy dokładne wnioskowanie HMM dla każdego kwadratu brudu niezależnie, uwarunkowane sekwencją lokalizacji w tej cząstce. Każda cząstka zawiera zatem próbkowane położenie plus 42 dokładne a posteriori dla 42 kwadratów — dokładnie, zakładając, że hipotetyczna trajektoria położenia, po której następuje ta cząstka, jest poprawna. To podejście, zwane filtrem cząstek Rao-Blackwellized, bez problemu radzi sobie z deterministycznym zabrudzeniem, stopniowo budując dokładną mapę brudu z dokładnym wykrywaniem lokalizacji lub wykrywaniem zaszumionych ścian, jak pokazano na rysunku (b). W przypadkach, które nie spełniają rodzaju warunkowej struktury niezależności, Rao-Blackwellization nie ma zastosowania. W uwagach na końcu wymieniono szereg algorytmów, które zostały zaproponowane do rozwiązania ogólnego problemu filtrowania ze zmiennymi statycznymi. Żaden z nich nie ma takiej elegancji i szerokiego zastosowania jak filtr cząstek, ale kilka z nich jest skutecznych w praktyce w niektórych klasach problemów.