Aby skonstruować DBN, należy określić trzy rodzaje informacji: uprzedni rozkład względem zmiennych stanu, P(X0); model przejściowy P(Xt+1 | Xt); oraz model czujnika P(Et | Xt). Aby sprecyzować modele tranzytowe i sensorowe, należy również określić topologię połączeń pomiędzy kolejnymi warstwami oraz pomiędzy zmiennymi stanu i dowodu. Ponieważ zakłada się, że modele przejścia i czujniki są jednorodne w czasie — takie same dla wszystkich t — najwygodniej jest po prostu określić je dla pierwszego wycinka. Na przykład, pełna specyfikacja DBN dla świata parasolowego jest podana przez sieć trójwęzłową pokazaną na rysunku (a).
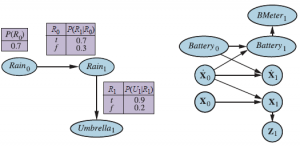
Na podstawie tej specyfikacji, kompletny DBN z nieograniczoną liczbą wycinków czasu może być skonstruowany według potrzeb poprzez skopiowanie pierwszego wycinka. Rozważmy teraz ciekawszy przykład: monitorowanie robota zasilanego bateryjnie poruszającego się w płaszczyźnie X–Y. Po pierwsze, potrzebujemy zmiennych stanu, które będą zawierać zarówno Xt =(Xt ,Yt) dla pozycji, jak i 
dla prędkości. Zakładamy, że pewna metoda pomiaru pozycji – na przykład kamera stała lub pokładowy GPS (Global Positioning System) – daje pomiary Zt . Pozycja w następnym kroku czasowym zależy od aktualnej pozycji i prędkości, tak jak w standardowym modelu filtra Kalmana. Prędkość w kolejnym kroku zależy od aktualnej prędkości i stanu baterii. Dodajemy Batteryt, aby przedstawić rzeczywisty poziom naładowania baterii, który ma za rodzica poprzedni poziom naładowania baterii i prędkość i dodajemy BMetert , który mierzy poziom naładowania baterii. Daje nam to podstawowy model pokazany na rysunku (b). Warto przyjrzeć się bliżej charakterowi modelu czujnika dla BMetert. Załóżmy dla uproszczenia, że zarówno Batteryt, jak i BMetert mogą przyjmować wartości dyskretne od 0 do 5. Jeśli miernik jest zawsze dokładny, wówczas CPT P(BMetert | Batteryt) powinien mieć prawdopodobieństwa 1,0 „wzdłuż przekątnej” i prawdopodobieństwa 0,0 w innych miejscach. W rzeczywistości do pomiarów zawsze wkrada się hałas. W przypadku pomiarów ciągłych można zastosować rozkład Gaussa z małą wariancją. W przypadku naszych zmiennych dyskretnych możemy przybliżyć rozkład Gaussa za pomocą rozkładu, w którym prawdopodobieństwo błędu spada w odpowiedni sposób, tak aby prawdopodobieństwo dużego błędu Jest bardzo mały. Używamy terminu model błędu Gaussa, aby objąć zarówno wersję ciągłą, jak i dyskretną. Model błędu Gaussa Każdy, kto ma praktyczne doświadczenie w robotyce, skomputeryzowanej kontroli procesu lub innych formach automatycznego wykrywania, z łatwością potwierdzi, że małe ilości szumu pomiarowego są często najmniejszym z problemów. Prawdziwe czujniki zawodzą. Kiedy czujnik ulegnie awarii, niekoniecznie wysyła sygnał mówiący: „A tak przy okazji, dane, które zamierzam wysłać, to stek bzdur”. Zamiast tego po prostu wysyła bzdury. Najprostszy rodzaj awarii nazywa się awarią przejściową, w której czujnik czasami decyduje się wysłać jakieś bzdury. W przypadku awarii przejściowej czujnik poziomu akumulatora może mieć zwyczaj wysyłania odczytu 0, gdy ktoś uderzy w robota, nawet jeśli akumulator jest w pełni naładowany. Zobaczmy, co się stanie, gdy wystąpi awaria przejściowa z modelem błędów Gaussa, który nie uwzględnia takich awarii. Załóżmy na przykład, że robot siedzi cicho i obserwuje 20 kolejnych odczytów baterii po 5. Następnie miernik baterii ma chwilowe zajęcie i następny odczyt to BMeter21=0. W co prosty model błędu Gaussa doprowadzi nas do przekonania o Battery21? Zgodnie z regułą Bayesa odpowiedź zależy zarówno od modelu czujnika P(BMeter21=0 | Battery21), jak i predykcji P(Battery21 | BMeter1:20). Jeśli prawdopodobieństwo dużego błędu czujnika jest znacznie mniejsze niż prawdopodobieństwo przejścia na Battery21=0, nawet jeśli to ostatnie jest bardzo mało prawdopodobne, to rozkład a posteriori przypisze wysokie prawdopodobieństwo rozładowania akumulatora. Drugi odczyt 0 przy t=22 sprawi, że ten wniosek będzie prawie pewny. Jeśli awaria przejściowa zniknie, a odczyt powróci do 5 od t=23 wzwyż, szacunkowy poziom baterii szybko powróci do 5. (Nie oznacza to, że algorytm myśli, że bateria została magicznie naładowana, co może być fizycznie niemożliwe; zamiast tego algorytm uważa teraz, że poziom naładowania baterii nigdy nie był niski, a skrajnie nieprawdopodobna hipoteza, że miernik baterii popełnił dwa kolejne ogromne błędy, musi być właściwym wyjaśnieniem). Ten przebieg wydarzeń ilustruje górna krzywa na rysunku (a), który pokazuje oczekiwaną wartość Batteryt w czasie, przy użyciu dyskretnego modelu błędu Gaussa.
Mimo powrotu do zdrowia jest czas (t=22), kiedy robot jest przekonany, że jego bateria jest rozładowana; przypuszczalnie w takim razie powinien wysłać sygnał mayday i zamknąć się. Niestety, zbyt uproszczony model czujnika sprowadził go na manowce.
Najprostszy model awarii czujnika pozwala na pewne prawdopodobieństwo, że czujnik zwróci zupełnie niepoprawną wartość, niezależnie od rzeczywistego stanu świata. Na przykład, jeśli miernik baterii zawiedzie, zwracając 0, możemy powiedzieć, że
P(Bmetert =0 |Batteryt =5)=0:03;
które jest prawdopodobnie znacznie większe niż prawdopodobieństwo przypisane przez prosty model błędu Gaussa. Nazwijmy to przejściowym modelem awarii. Jak to pomaga, gdy mamy do czynienia z odczytem 0? Zakładając, że przewidywane prawdopodobieństwo rozładowania baterii, zgodnie z dotychczasowymi odczytami, jest znacznie mniejsze niż 0,03, najlepszym wyjaśnieniem obserwacji BMeter21=0 jest chwilowa awaria czujnika. Intuicyjnie możemy myśleć o przekonaniu o poziomie naładowania baterii jako o pewnej „bezwładności”, która pomaga przezwyciężyć tymczasowe skoki w odczycie licznika. Górna krzywa na rysunku (b) pokazuje, że model awarii przejściowych może obsługiwać awarie przejściowe bez katastrofalnej zmiany przekonań. Tyle o tymczasowych błędach. A co z uporczywą awarią czujnika Niestety, tego rodzaju awarie są zbyt częste. Jeśli czujnik zwróci 20 odczytów na 5, a następnie 20 odczytów na 0, wówczas model tymczasowej awarii czujnika opisany w poprzednim akapicie spowoduje, że robot stopniowo zacznie wierzyć, że jego bateria jest rozładowana, podczas gdy w rzeczywistości może się okazać, że miernik przegrany. Dolna krzywa na rysunku 14.14(b) pokazuje „trajektorię” przekonania dla tego przypadku. Przy t=25 — pięciu odczytach równych 0 — robot jest przekonany, że jego bateria jest rozładowana. Oczywiście wolelibyśmy, aby robot uwierzył, że jego licznik baterii jest uszkodzony — jeśli rzeczywiście jest to bardziej prawdopodobne zdarzenie. Nic dziwnego, że do obsługi trwałych awarii potrzebujemy modelu trwałej awarii, który opisuje zachowanie czujnika w normalnych warunkach i po awarii. Aby to zrobić, musimy uzupełnić stan systemu o dodatkową zmienną, powiedzmy BMBroken, która opisuje stan miernika baterii. Utrzymywanie się awarii musi być modelowane przez łuk łączący BMBroken0 z BMBroken1. Ten łuk trwałości ma CPT, który daje małe prawdopodobieństwo awarii łuku trwałości w dowolnym kroku czasowym, powiedzmy 0,001, ale określa, że czujnik pozostaje uszkodzony po jego zerwaniu. Gdy czujnik jest w porządku, model czujnika dla BMeter jest identyczny z modelem awarii przejściowej; gdy czujnik jest uszkodzony, mówi, że BMeter zawsze wynosi 0, niezależnie od rzeczywistego poziomu naładowania baterii. Model trwałej awarii czujnika akumulatora pokazano na rysunku (a).
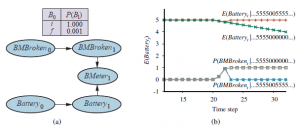
Jego działanie w dwóch sekwencjach danych (przejściowy impuls i trwała awaria) pokazano na rysunku (b). Jest kilka rzeczy, które należy zwrócić uwagę na te krzywe. Po pierwsze, w przypadku chwilowego piku prawdopodobieństwo uszkodzenia czujnika znacznie wzrasta po drugim odczycie 0, ale natychmiast spada do zera po zaobserwowaniu 5. Po drugie, w przypadku uporczywej awarii prawdopodobieństwo uszkodzenia czujnika szybko wzrasta do prawie 1 i tam pozostaje. Wreszcie, gdy wiadomo, że czujnik jest uszkodzony, robot może jedynie założyć, że jego bateria rozładowuje się w „normalnym” tempie. Świadczy o tym stopniowo obniżający się poziom E (Batteryt |…). Do tej pory jedynie zarysowaliśmy powierzchnię problemu przedstawiania złożonych procesów. Różnorodność modeli przejściowych jest ogromna i obejmuje tak różne tematy, jak modelowanie układu hormonalnego człowieka i modelowanie wielu pojazdów poruszających się po autostradzie. Modelowanie sensorów jest również samo w sobie obszernym poddziedziną. Jednak dynamiczne sieci bayesowskie mogą modelować nawet subtelne zjawiska, takie jak dryf czujnika, nagła dekalibracja i wpływ warunków egzogenicznych (takich jak pogoda) na odczyty czujnika.