Filtr Kalmana i jego opracowania są wykorzystywane w szerokiej gamie zastosowań. „Klasyczne” zastosowanie to radarowe śledzenie samolotów i pocisków. Powiązane zastosowania obejmują śledzenie akustyczne okrętów podwodnych i pojazdów naziemnych oraz wizualne śledzenie pojazdów i ludzi. W nieco bardziej ezoterycznej żyle filtry Kalmana służą do rekonstrukcji trajektorii cząstek na podstawie zdjęć z komór bąbelkowych i prądów oceanicznych z pomiarów powierzchni satelitów. Zakres zastosowań jest znacznie większy niż tylko śledzenie ruchu: wystarczy każdy system charakteryzujący się ciągłymi zmiennymi stanu i zaszumionymi pomiarami. Takie systemy obejmują celulozownie, zakłady chemiczne, reaktory jądrowe, ekosystemy roślinne i gospodarki narodowe. Fakt, że filtrowanie Kalmana można zastosować do systemu, nie oznacza, że wyniki będą prawidłowe lub użyteczne. Poczynione założenia — modele liniowego przejścia Gaussa i modele czujników — są bardzo mocne. Rozszerzony filtr Kalmana (EKF) próbuje przezwyciężyć nieliniowości w modelowanym systemie. System jest nieliniowy, jeśli modelu przejścia nie można opisać jako mnożenia macierzy wektora stanu, jak w równaniu .EKF działa poprzez modelowanie systemu jako lokalnie liniowego w xt w obszarze xt = μt , czyli średniej bieżącego rozkładu stanu. Działa to dobrze w przypadku płynnych, dobrze zachowujących się systemów i pozwala trackerowi utrzymywać i aktualizować rozkład stanu Gaussa, który jest rozsądnym przybliżeniem do prawdziwego a posteriori. Co to znaczy, że system jest „niegładki” lub „źle zachowywany”? Z technicznego punktu widzenia oznacza to, że istnieje znacząca nieliniowość w odpowiedzi systemu w obszarze, który jest „bliski” (zgodnie z kowariancją Σt ) do aktualnej średniej μt . Aby zrozumieć tę ideę w kategoriach nietechnicznych, rozważ przykład próby wyśledzenia ptaka przelatującego przez dżunglę. Wydaje się, że ptak zmierza z dużą prędkością prosto w pień drzewa. Filtr Kalmana, regularny lub rozszerzony, może jedynie przewidywać położenie ptaka, a średnia tego Gaussa będzie wyśrodkowana na pniu, jak pokazano na rysunku (a). Z drugiej strony, rozsądny model ptaka przewidziałby uniknięcie z jednej lub drugiej strony, jak pokazano na rysunku (b). Taki model jest wysoce nieliniowy, ponieważ decyzja ptaka jest bardzo zróżnicowana w zależności od jego dokładnego położenia względem pnia.
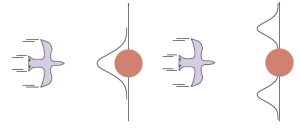
Do obsługi takich przykładów wyraźnie potrzebujemy bardziej wyrazistego języka do reprezentowania zachowania modelowanego systemu. W społeczności teorii sterowania, w przypadku której problemy, takie jak manewrowanie z wymijaniem przez samoloty, wiążą się z podobnymi trudnościami, standardowym rozwiązaniem jest przełączający filtr Kalmana. W tym podejściu wiele filtrów Kalmana działa równolegle, z których każdy wykorzystuje inny model systemu — na przykład jeden do lotu prostego, jeden do ostrych skrętów w lewo i jeden do ostrych skrętów w prawo. Używana jest ważona suma prognoz, w której waga zależy od tego, jak dobrze każdy filtr pasuje do bieżących danych. W następnej sekcji zobaczymy, że jest to po prostu szczególny przypadek ogólnego dynamicznego modelu sieci bayesowskiej, uzyskany przez dodanie dyskretnej zmiennej stanu „manewru” do sieci.