Powyższe wyprowadzenie ilustruje kluczową właściwość rozkładów Gaussa, która umożliwia działanie filtrowania Kalmana: fakt, że wykładnik jest formą kwadratową. Dotyczy to nie tylko przypadku jednowymiarowego; pełny wielowymiarowy rozkład Gaussa ma postać
![]()
Mnożąc wyrazy w wykładniku, widzimy, że wykładnik jest również funkcją kwadratową wartości xi w x. W ten sposób filtrowanie zachowuje gaussowski charakter rozkładu stanu. Najpierw zdefiniujmy ogólny model czasowy używany z filtrowaniem Kalmana. Zarówno model przejściowy, jak i model czujnika muszą być transformacją liniową z dodatkiem szumu Gaussa. Tak więc mamy
![]()
gdzie F i Σx są macierzami opisującymi model przejścia liniowego i kowariancją szumu przejścia, a H i Σz są odpowiednimi macierzami dla modelu czujnika. Teraz zaktualizowane równania dla średniej i kowariancji, w ich pełnej, włochatej okropności, to
![]()
gdzie
![]() jest macierzą wzmocnienia Kalmana. Niezależnie od tego, czy wierzysz czy nie , równania te mają jakiś intuicyjny sens. Rozważmy na przykład aktualizację oszacowania średniego stanu μ. Termin Fμt jest przewidywanym stanem w t +1, więc HFμt jest przewidywaną obserwacją. Dlatego termin zt+1 – HFμt reprezentuje błąd w przewidywanej obserwacji. Jest to mnożone przez Kt+1 w celu skorygowania przewidywanego stanu; stąd Kt+1 jest miarą tego, jak poważnie należy traktować nową obserwację w stosunku do przewidywania. Podobnie jak w równaniu , mamy również własność, że aktualizacja wariancji jest niezależna od obserwacji. Sekwencję wartości Σt i Kt można zatem obliczyć w trybie offline, a rzeczywiste obliczenia wymagane podczas śledzenia w trybie online są dość skromne. Aby zilustrować działanie tych równań, zastosowaliśmy je do problemu śledzenia obiektu poruszającego się na płaszczyźnie X–Y. Zmienne stanu to
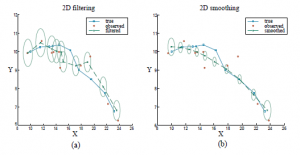
jest macierzą wzmocnienia Kalmana. Niezależnie od tego, czy wierzysz czy nie , równania te mają jakiś intuicyjny sens. Rozważmy na przykład aktualizację oszacowania średniego stanu μ. Termin Fμt jest przewidywanym stanem w t +1, więc HFμt jest przewidywaną obserwacją. Dlatego termin zt+1 – HFμt reprezentuje błąd w przewidywanej obserwacji. Jest to mnożone przez Kt+1 w celu skorygowania przewidywanego stanu; stąd Kt+1 jest miarą tego, jak poważnie należy traktować nową obserwację w stosunku do przewidywania. Podobnie jak w równaniu , mamy również własność, że aktualizacja wariancji jest niezależna od obserwacji. Sekwencję wartości Σt i Kt można zatem obliczyć w trybie offline, a rzeczywiste obliczenia wymagane podczas śledzenia w trybie online są dość skromne. Aby zilustrować działanie tych równań, zastosowaliśmy je do problemu śledzenia obiektu poruszającego się na płaszczyźnie X–Y. Zmienne stanu to ![]() więc F, Σx, H i Σz to macierze 4 x 4. Rysunek (a) pokazuje prawdziwą trajektorię, serię zaszumionych obserwacji i trajektorię oszacowaną przez filtrowanie Kalmana, wraz z kowariancjami wskazanymi przez kontury z jednym odchyleniem standardowym. Proces filtrowania dobrze sprawdza się w śledzeniu rzeczywistego ruchu i zgodnie z oczekiwaniami wariancja szybko osiąga ustalony punkt. Możemy również wyprowadzić równania do wygładzania i filtrowania za pomocą modeli liniowo-gaussowskich. Wyniki wygładzania pokazano na rysunku (b). Zwróć uwagę, jak wariancja oszacowania pozycji jest znacznie zmniejszona, z wyjątkiem końców trajektorii (dlaczego?) i że oszacowana trajektoria jest znacznie gładsza.
więc F, Σx, H i Σz to macierze 4 x 4. Rysunek (a) pokazuje prawdziwą trajektorię, serię zaszumionych obserwacji i trajektorię oszacowaną przez filtrowanie Kalmana, wraz z kowariancjami wskazanymi przez kontury z jednym odchyleniem standardowym. Proces filtrowania dobrze sprawdza się w śledzeniu rzeczywistego ruchu i zgodnie z oczekiwaniami wariancja szybko osiąga ustalony punkt. Możemy również wyprowadzić równania do wygładzania i filtrowania za pomocą modeli liniowo-gaussowskich. Wyniki wygładzania pokazano na rysunku (b). Zwróć uwagę, jak wariancja oszacowania pozycji jest znacznie zmniejszona, z wyjątkiem końców trajektorii (dlaczego?) i że oszacowana trajektoria jest znacznie gładsza.