Powiedzieliśmy, że operator FORWARD dla filtru Kalmana odwzorowuje gaussowskie na nowe gaussowskie. Przekłada się to na obliczenie nowej średniej i kowariancji z poprzedniej średniej i kowariancji. Wyprowadzenie reguły aktualizacji w ogólnym (wielowymiarowym) przypadku wymaga dość dużo algebry liniowej, więc na razie będziemy trzymać się bardzo prostego przypadku jednowymiarowego, a później podamy wyniki dla przypadku ogólnego. Nawet dla przypadku jednowymiarowego obliczenia są nieco żmudne, ale uważamy, że warto je zobaczyć, ponieważ użyteczność filtra Kalmana jest tak ściśle powiązana z matematycznymi właściwościami rozkładów Gaussa. Rozważany przez nas model czasowy opisuje błądzenie losowe pojedynczej ciągłej zmiennej stanu Xt z zaszumioną obserwacją Zt . Przykładem może być wskaźnik „zaufania konsumentów”, który można modelować jako przechodzący co miesiąc losową zmianę w rozkładzie gaussowskim i który jest mierzony za pomocą losowej ankiety konsumenckiej, która wprowadza również szum próbkowania gaussowski. Zakłada się, że poprzedni rozkład jest gaussowski z wariancją σ20:
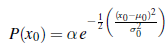
(Dla uproszczenia używamy tego samego symbolu α dla wszystkich stałych normalizujących w tej sekcji). Model przejściowy dodaje zaburzenie Gaussa o stałej wariancji σ2x do bieżącego stanu:
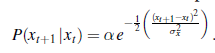
Model czujnika zakłada szum Gaussa z wariancją σ2z :
![]()
Teraz, biorąc pod uwagę poprzednie P(X0), jednostopniowy rozkład przewidziany pochodzi z równania
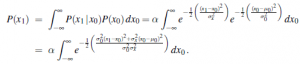
Ta całka wygląda na dość skomplikowaną. Kluczem do postępu jest zauważenie, że wykładnik jest sumą dwóch wyrażeń, które są kwadratowe w x0, a zatem sam jest kwadratem w x0. Prosta sztuczka znana jako uzupełnianie kwadratu pozwala na przepisanie dowolnego kwadratu ax20 +bx0+c jako Uzupełnienie kwadratu sumy kwadratu składnika a(x0 – -b/2a)2 i składnika resztkowego c – b2/4a, który jest niezależny od x0. W tym przypadku mamy a=( σ20 + σ2x )/( σ20 σ2 ), b = -2(σ20x1 + σ2x μ0)/( σ20 σ2x ) i c=( σ20x21 + σ2x μ20 )/( σ20 σ2x ). Człon resztkowy można wziąć poza całkę, co daje nam
![]()
Teraz całka jest po prostu całką Gaussa w całym jego zakresie, czyli po prostu 1. Tak więc pozostaje nam tylko człon rezydualny z kwadratu. Wstawiając z powrotem wyrażenia dla a, b i c i upraszczając, otrzymujemy
![]()
Oznacza to, że jednoetapowy rozkład przewidziany jest rozkładem Gaussa z taką samą średnią μ0 i wariancją równą sumie oryginalnej wariancji σ20 i wariancji przejścia σ2x . Aby zakończyć krok aktualizacji, musimy uzależnić obserwację w pierwszym kroku czasowym, czyli z1. Z równania jest to
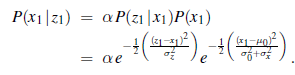
Jeszcze raz łączymy wykładniki i uzupełniamy kwadrat, otrzymując następujące wyrażenie dla tyłu:
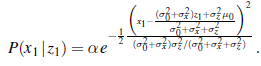
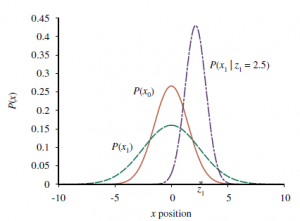
Tak więc po jednym cyklu aktualizacji mamy nowy rozkład Gaussa dla zmiennej stanu. Ze wzoru Gaussa w równaniu widzimy, że nową średnią i odchylenie standardowe można obliczyć na podstawie starej średniej i odchylenia standardowego w następujący sposób:
![]()
Rysunek przedstawia jeden cykl aktualizacji filtru Kalmana w przypadku jednowymiarowym dla poszczególnych wartości modeli przejścia i czujników.
Równanie pełni dokładnie taką samą rolę jak ogólne równanie filtrowania lub równanie filtrowania HMM . Jednak ze względu na szczególną naturę rozkładów Gaussa, równania te mają kilka interesujących dodatkowych właściwości. Po pierwsze, możemy zinterpretować obliczenia dla nowej średniej μt+1 jako średnią ważoną nowej obserwacji zt+1 i starej średniej μt . Jeśli obserwacja jest zawodna, to σ2z jest duże i zwracamy większą uwagę na starą średnią; jeśli stara średnia jest zawodna ( σ2t jest duża) lub proces jest wysoce nieprzewidywalny ( σ2x jest duża), to zwracamy większą uwagę na obserwację. Po drugie, zauważ, że aktualizacja wariancji σ2t+1 jest niezależna od obserwacji. Możemy zatem z góry obliczyć, jaka będzie kolejność wartości wariancji. Po trzecie, sekwencja wartości wariancji szybko zbliża się do stałej wartości, która zależy tylko od σ2x i σ2z, co znacznie upraszcza dalsze obliczenia.