Wygładzanie

Jak powiedzieliśmy wcześniej, wygładzanie jest procesem obliczania rozkładu po stanach przeszłych, których dane dotyczą do chwili obecnej – to znaczy P(X_k je_1:t) dla 0 ≤  k

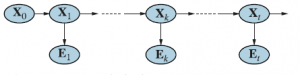
W oczekiwaniu na inne rekurencyjne podejście do przekazywania komunikatów, możemy podzielić obliczenia na dwie części — dowód do k i dowód od k+1 do t,

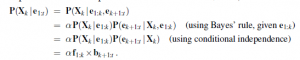
gdzie „X” oznacza punktowe mnożenie wektorów. Tutaj zdefiniowaliśmy komunikat „wstecz” b_k+1:t =P(e  | X_k), analogiczny do komunikatu w przód f_1:k. Komunikat do przodu f_1:k można obliczyć przez filtrowanie w przód od 1 do k, zgodnie z równaniem. Okazuje się, że wiadomość wstecz b_k+1:t może być obliczona przez proces rekurencyjny, który działa wstecz od t:

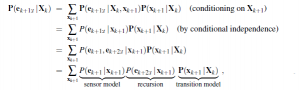
gdzie po ostatnim kroku następuje warunkowa niezależność e_k+1 i e_k+2:t , przy danym x_k+1. W tym wyrażeniu wszystkie terminy pochodzą albo z modelu, albo z poprzedniej wiadomości wstecznej. Stąd mamy pożądane sformułowanie rekurencyjne. W formie wiadomości mamy

gdzie BACKWARD implementuje aktualizację opisaną w Równaniu. Podobnie jak w przypadku rekurencji do przodu, czas i przestrzeń potrzebne do każdej aktualizacji są stałe, a zatem niezależne od t. Widzimy teraz, że oba wyrazy w równaniu  mogą być obliczone przez rekursje w czasie, jeden biegnący w przód od 1 do k i używający równania filtrującego  i drugi biegnący wstecz od t do k+1 i używający Równanie (14.9). Dla inicjalizacji fazy wstecznej mamy b_t+1:t =P(e_t+1:t | X_t)=P( |X_t)=1, gdzie 1 jest wektorem 1s. Powodem tego jest to, że e_t+1:t jest ciągiem pustym, więc prawdopodobieństwo jego zaobserwowania wynosi 1. Zastosujmy teraz ten algorytm do przykładu parasolowego, obliczając wygładzone oszacowanie prawdopodobieństwa deszczu w czasie k=1 , biorąc pod uwagę obserwacje parasola w dniach 1 i 2. Z równania, jest to podane przez

Pierwszym terminem, o którym już wiemy, jest <.818,.182>, z procesu filtrowania w przód opisanego wcześniej. Drugi składnik można obliczyć, stosując rekurencję wsteczną w równaniu:

Podstawiając to do równania, okazuje się, że wygładzone oszacowanie deszczu w dniu 1 wynosi

Zatem wygładzone oszacowanie dla deszczu pierwszego dnia jest w tym przypadku wyższe niż oszacowanie filtrowane (0,818). Dzieje się tak, ponieważ parasol w dniu 2 sprawia, że ​​bardziej prawdopodobne jest, że padał deszcz drugiego dnia; z kolei, ponieważ deszcz ma tendencję do utrzymywania się, jest bardziej prawdopodobne, że padał pierwszego dnia. Zarówno rekursja do przodu, jak i do tyłu zajmują stałą ilość czasu na krok; stąd złożoność czasowa wygładzania w odniesieniu do dowodu e_1:t wynosi O(t). Jest to złożoność wygładzania w określonym kroku czasowym k. Jeśli chcemy wygładzić całą sekwencję, jedną oczywistą metodą jest po prostu uruchomienie całego procesu wygładzania raz dla każdego kroku czasowego, który ma być wygładzony. Powoduje to złożoność czasową O(t²). Lepsze podejście wykorzystuje proste zastosowanie programowania dynamicznego w celu zmniejszenia złożoności do O(t). Wskazówka pojawia się w poprzedniej analizie przykładu parasolowego, w którym mogliśmy ponownie wykorzystać wyniki fazy filtrowania do przodu. Kluczem do algorytmu czasu liniowego jest rejestrowanie wyników filtrowania w przód w całej sekwencji. Następnie uruchamiamy rekursję wsteczną od t do 1, obliczając wygładzone oszacowanie w każdym kroku k z obliczonej wiadomości wstecznej b_k+1:t i zapisanej wiadomości przesyłanej do przodu f_1:k. Algorytm, trafnie nazywany algorytmem naprzód-wstecz, pokazano

Czytnik alertów zauważył, że struktura sieci bayesowskiej to wielodrzewo . Oznacza to, że proste zastosowanie algorytmu grupowania daje również algorytm czasu liniowego, który oblicza wygładzone szacunki dla całej sekwencji. Obecnie rozumie się, że algorytm naprzód-wstecz jest w rzeczywistości szczególnym przypadkiem algorytmu propagacji wielodrzewa używanego z metodami grupowania (chociaż oba zostały opracowane niezależnie). Algorytm naprzód-wstecz stanowi podstawę obliczeniową dla wielu aplikacji, które zajmują się sekwencjami zaszumionych obserwacji. Jak opisano do tej pory, ma dwie praktyczne wady. Po pierwsze, jego złożoność przestrzenna może być zbyt wysoka, gdy przestrzeń stanów jest duża, a sekwencje długie. Wykorzystuje przestrzeń O(|f|t), gdzie |f| jest rozmiarem reprezentacji przekazywanej wiadomości. Zapotrzebowanie na miejsce można zredukować do O(|f|logt) przy jednoczesnym wzroście złożoności czasowej o współczynnik logt, jak pokazano w ćwiczeniu. W niektórych przypadkach można użyć algorytmu przestrzeni stałej. Drugą wadą podstawowego algorytmu jest to, że wymaga on modyfikacji, aby działał w trybie online, w którym wygładzone oszacowania muszą być obliczane dla wcześniejszych przedziałów czasu, ponieważ nowe obserwacje są stale dodawane na końcu sekwencji. Najczęstszym wymaganiem jest wygładzanie ze stałym opóźnieniem, które wymaga obliczenia wygładzonej oceny P(Xt􀀀d je1:t) Wygładzanie ze stałym opóźnieniem dla stałego d. Oznacza to, że wygładzanie jest wykonywane dla odcinka czasu d o krok za bieżącym czasem t; wraz ze wzrostem t wygładzanie musi nadążyć. Oczywiście możemy uruchomić algorytm naprzód-wstecz w „oknie” kroku d, gdy dodawana jest każda nowa obserwacja, ale wydaje się to nieefektywne.