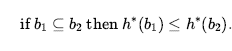Miesiąc: marzec 2022

Rozważmy przykład niepewnego rozumowania: diagnozowanie bólu zęba u dentysty. Diagnoza – czy to w medycynie, naprawie samochodu, czy cokolwiek – prawie zawsze wiąże się z niepewnością. Spróbujmy napisać zasady diagnostyki stomatologicznej za pomocą logiki zdań, abyśmy mogli zobaczyć, jak załamuje się podejście logiczne. Rozważ następującą prostą zasadę:

Problem w tym, że ta zasada jest błędna. Nie wszyscy pacjenci z bólami zębów mają ubytki; niektóre z nich mają chorobę dziąseł, ropień lub jeden z kilku innych problemów:

Niestety, aby reguła była prawdziwa, musimy dodać niemal nieograniczoną listę możliwych problemów. Możemy spróbować zmienić regułę w regułę przyczynową:

Ale ta zasada też nie jest słuszna; nie wszystkie ubytki powodują ból. Jedynym sposobem na naprawienie tej zasady jest uczynienie jej logicznie wyczerpującą: uzupełnić lewą stronę o wszystkie kwalifikacje wymagane do tego, aby ubytek powodował ból zęba. Próba użycia logiki do radzenia sobie z dziedziną, taką jak diagnoza medyczna, kończy się niepowodzeniem z trzech głównych powodów:

* LENISTWO: Wyliczenie pełnego zestawu poprzedników lub następników potrzebnych do zapewnienia bezwyjątkowej reguły jest zbyt dużo pracy i zbyt trudne jest stosowanie takich reguł.

* IGNORANCJA TEORETYCZNA: Medycyna nie ma pełnej teorii w tej dziedzinie.

* PRAKTYCZNA IGNORANCJA: Nawet jeśli znamy wszystkie zasady, możemy być niepewni co do konkretnego pacjenta, ponieważ nie wszystkie niezbędne testy zostały lub mogą być przeprowadzone.

Związek między bólami zębów a próchnicą nie jest ściśle logiczną konsekwencją w żadnym kierunku. Jest to typowe dla dziedziny medycyny, jak również większości innych dziedzin osądzania: prawa, biznesu, projektowania, naprawy samochodów, ogrodnictwa, randek i tak dalej. Wiedza agenta może w najlepszym razie zapewnić tylko pewien stopień wiary w odpowiednie zdania. Naszym głównym narzędziem do radzenia sobie ze stopniami wiary jest teoria prawdopodobieństwa. W terminologii zobowiązania ontologiczne logiki i teorii prawdopodobieństwa są takie same – że świat składa się z faktów, które obowiązują lub nie w żadnym konkretnym przypadku – ale zobowiązania epistemologiczne są różne: podmiot logiczny wierzy w każde zdanie być prawdziwe lub fałszywe lub nie ma opinii, podczas gdy czynnik probabilistyczny może mieć liczbowy stopień wiary między 0 (dla zdań, które są z pewnością fałszywe) a 1 (z pewnością prawdziwe). Teoria prawdopodobieństwa dostarcza sposobu podsumowania niepewności, która pochodzi z naszego lenistwa i ignorancji, rozwiązując w ten sposób problem kwalifikacji. Możemy nie wiedzieć na pewno, co dotyka konkretnego pacjenta, ale uważamy, że istnieje, powiedzmy, 80% prawdopodobieństwo, czyli prawdopodobieństwo 0,8, że pacjent, który cierpi na ból zęba, ma ubytek. Oznacza to, że oczekujemy, że spośród wszystkich sytuacji, które według naszej wiedzy są nie do odróżnienia od obecnej, pacjent będzie miał ubytek w 80% z nich. Przekonanie to można wyprowadzić z danych statystycznych — 80% pacjentów z bólem zęba, których do tej pory widziano, miało ubytki — lub z ogólnej wiedzy dentystycznej lub z kombinacji źródeł dowodowych. Mylące jest to, że w momencie postawienia diagnozy nie ma niepewności w rzeczywistym świecie: pacjent albo ma ubytek, albo go nie ma. Więc co to znaczy, że prawdopodobieństwo ubytku wynosi 0,8? Czy nie powinno być 0 czy 1? Odpowiedź brzmi, że twierdzenia prawdopodobieństwa są tworzone w odniesieniu do stanu wiedzy, a nie w odniesieniu do świata rzeczywistego. Mówimy: „Prawdopodobieństwo, że pacjentka ma ubytek, biorąc pod uwagę ból zęba, wynosi 0,8”. Jeśli później dowiemy się, że pacjentka cierpiała na chorobę dziąseł, możemy wypowiedzieć się inaczej: „Prawdopodobieństwo, że pacjentka ma ubytek, biorąc pod uwagę ból zęba i historię choroby dziąseł, wynosi 0,4”. Jeśli zbierzemy dalsze rozstrzygające dowody przeciwko ubytkowi, możemy powiedzieć: „Prawdopodobieństwo, że pacjent ma ubytek, biorąc pod uwagę wszystko, co wiemy, wynosi prawie 0”. Zauważ, że te stwierdzenia nie są ze sobą sprzeczne; każdy jest oddzielnym stwierdzeniem o innym stanie wiedzy.

Agenci w świecie rzeczywistym muszą radzić sobie z niepewnością, czy to z powodu częściowej obserwowalności, niedeterminizmu, czy przeciwników. Agent może nigdy nie wiedzieć na pewno, w jakim stanie się teraz znajduje lub dokąd trafi po wykonaniu sekwencji działań. Widzieliśmy, jak rozwiązujący problemy i logiczni agenci radzą sobie z niepewnością, śledząc stan przekonań – reprezentację zbioru wszystkich możliwych stanów świata, w których może się on znajdować – i generując plan awaryjny, który uwzględnia każdą możliwą ewentualność, którą mogą zgłaszać czujniki podczas wykonywania. To podejście działa w przypadku prostych problemów, ale ma wady:

* Agent musi rozważyć wszystkie możliwe wyjaśnienia swoich obserwacji czujnika, bez względu na to, jak mało prawdopodobne jest. Prowadzi to do dużego stanu wiary, pełnego nieprawdopodobnych możliwości.

* Prawidłowy plan warunkowy, który radzi sobie z każdą ewentualnością, może wzrosnąć dowolnie duży i musi rozważyć arbitralnie mało prawdopodobne sytuacje.

* Czasem nie ma planu gwarantującego osiągnięcie celu – a jednak agent musi działać. Musi mieć jakiś sposób na porównanie zalet planów, które nie są gwarantowane.

Załóżmy na przykład, że zautomatyzowana taksówka ma na celu dostarczenie pasażera na lotnisko na czas. Taksówka układa plan, A₉₀ , który zakłada opuszczenie domu 90 minut przed odlotem i jazdę z rozsądną prędkością. Mimo że lotnisko jest oddalone o zaledwie 8 mil, logiczny agent nie będzie w stanie stwierdzić z absolutną pewnością, że „Plan dowiezie nas na lotnisko na czas”. Zamiast tego dochodzi do słabszego wniosku „Plan dowiezie nas na lotnisko na czas, o ile samochód się nie zepsuje, a ja nie ulegnę wypadkowi, a droga nie jest zamknięta i nie ma meteorytu uderza w samochód i ….” Żaden z tych warunków nie może być wydedukowany na pewno, więc nie możemy wnioskować, że plan się powiedzie. Jest to problem logicznej kwalifikacji, dla którego do tej pory nie widzieliśmy żadnego realnego rozwiązania.

Niemniej jednak w pewnym sensie A90 jest w rzeczywistości słuszną rzeczą do zrobienia. Co przez to rozumiemy? Jak omówiliśmy w rozdziale 2, mamy na myśli, że spośród wszystkich planów, które można zrealizować, oczekuje się, że A90 zmaksymalizuje miarę wydajności agenta (gdzie oczekiwanie jest powiązane z wiedzą agenta o środowisku). Miara wydajności obejmuje dotarcie na lotnisko na czas przed lotem, unikanie długiego, bezproduktywnego oczekiwania na lotnisku oraz unikanie mandatów za przekroczenie prędkości po drodze. Wiedza agenta nie może zagwarantować żadnego z tych wyników dla A90, ale może zapewnić pewien stopień wiary, że zostaną one osiągnięte. Inne plany, takie jak A180, mogą zwiększyć przekonanie agenta, że ​​dotrze na lotnisko na czas, ale też zwiększyć prawdopodobieństwo długiego, nudnego oczekiwania. Właściwa rzecz do zrobienia – racjonalna decyzja – zależy zatem zarówno od względnej wagi różnych celów, jak i prawdopodobieństwa ich osiągnięcia oraz stopnia ich osiągnięcia. Pozostała część tej sekcji doskonali te idee, przygotowując się do rozwoju ogólnych teorii niepewnego rozumowania i racjonalnych decyzji.

Opisaliśmy reprezentację PDDL zarówno dla klasycznych, jak i rozszerzonych problemów planowania oraz przedstawiliśmy kilka algorytmicznych podejść do znajdowania rozwiązań. Punkty do zapamiętania:

* Systemy planowania to algorytmy rozwiązywania problemów, które operują na jawnie podzielonych na czynniki reprezentacjach stanów i działań. Reprezentacje te umożliwiają wyprowadzenie skutecznych heurystyk niezależnych od domeny oraz opracowanie potężnych i elastycznych algorytmów rozwiązywania problemów.

* PDDL, język definicji domeny planowania, opisuje stan początkowy i stan celu jako koniunkcje literałów i działań w kategoriach ich warunków wstępnych i skutków. Rozszerzenia reprezentują czas, zasoby, spostrzeżenia, plany warunkowe i plany hierarchiczne.

* Wyszukiwanie w przestrzeni stanów może działać w kierunku do przodu (postęp) lub do tyłu (regresja). Skuteczne heurystyki można wyprowadzić na podstawie założeń niezależności podrzędnych celów i różnych rozluźnień problemu planowania.

* Inne podejścia obejmują kodowanie problemu planowania jako problemu spełnialności Boole’a lub jako problemu spełniania ograniczeń; i jawne przeszukiwanie przestrzeni częściowo uporządkowanych planów.

* Hierarchiczne planowanie sieci zadań (HTN) pozwala agentowi uzyskać porady od projektanta domeny w postaci działań wysokiego poziomu (HLA), które można zaimplementować na różne sposoby za pomocą sekwencji działań niższego poziomu. Skutki HLA można zdefiniować za pomocą semantyki anielskiej, co pozwala na wyprowadzenie poprawnych planów wysokiego poziomu w sposób możliwy do udowodnienia bez uwzględniania implementacji niższego poziomu. Metody HTN mogą tworzyć bardzo duże plany wymagane przez wiele rzeczywistych aplikacji.

* Plany warunkowe pozwalają agentowi wyczuć świat podczas wykonywania, aby zdecydować, którą gałąź planu należy wykonać. W niektórych przypadkach planowanie bezczujnikowe lub zgodne może być wykorzystane do skonstruowania planu, który działa bez potrzeby percepcji. Zarówno plany zgodne, jak i warunkowe mogą być konstruowane poprzez poszukiwanie w przestrzeni stanów przekonań. Efektywna reprezentacja lub obliczanie stanów przekonań jest kluczowym problemem.

* Agent planowania online wykorzystuje monitorowanie wykonania i sploty w naprawach zgodnie z potrzebami, aby odzyskać sprawność po nieoczekiwanych sytuacjach, które mogą być spowodowane niedeterministycznymi działaniami, zdarzeniami egzogenicznymi lub nieprawidłowymi modelami środowiska.

* Wiele akcji zużywa zasoby, takie jak pieniądze, gaz lub surowce. Wygodnie jest traktować te zasoby jako miary liczbowe w puli, a nie próbować wnioskować na temat, powiedzmy, każdej monety i banknotu na świecie. Czas jest jednym z najważniejszych zasobów. Może być obsługiwany przez wyspecjalizowane algorytmy planowania lub planowanie może być zintegrowane z planowaniem.

* Rozszerzamy klasyczne planowanie na środowiska niedeterministyczne (gdzie wyniki działań są niepewne), ale nie jest to ostatnie słowo na temat planowania. Rozdział 17 opisuje techniki dla środowisk stochastycznych (w których wyniki działań mają związane z nimi prawdopodobieństwa): procesy decyzyjne Markowa, procesy decyzyjne Markowa częściowo obserwowalne oraz teoria gier.

Planowanie łączy dwa główne obszary sztucznej inteligencji, które omówiliśmy do tej pory: wyszukiwanie i logikę. Planista może być postrzegany albo jako program, który szuka rozwiązania, albo jako taki, który (konstruktywnie) udowadnia istnienie rozwiązania. Wzajemne inspirowanie się pomysłami z tych dwóch obszarów pozwoliło planistom na zwiększenie skali od problemów z zabawkami, w których liczba działań i stanów była ograniczona do kilkunastu, do rzeczywistych zastosowań przemysłowych z milionami stanów i tysiącami działań. Planowanie to przede wszystkim ćwiczenie w kontrolowaniu wybuchu kombinatorycznego. Jeżeli w domenie są zdania, to jest 2ⁿ stanów. W obliczu takiego pesymizmu identyfikacja niezależnych podproblemów może być potężną bronią. W najlepszym przypadku – pełnej dekompozycji problemu – otrzymujemy przyspieszenie wykładnicze. Rozkład jest jednak niszczony przez negatywne interakcje między działaniami. SATPLAN może kodować logiczne relacje między podproblemami. Wyszukiwanie do przodu rozwiązuje problem heurystycznie, próbując znaleźć wzorce (podzbiory zdań), które obejmują niezależne podproblemy. Ponieważ to podejście jest heurystyczne, może działać nawet wtedy, gdy podproblemy nie są całkowicie niezależne. Niestety, nie mamy jeszcze jasnego zrozumienia, które techniki najlepiej sprawdzają się w poszczególnych rodzajach problemów. Całkiem możliwe, że pojawią się nowe techniki, być może dostarczające syntezy wysoce ekspresyjnych reprezentacji pierwszego rzędu i hierarchicznych z wysoce wydajnymi reprezentacjami czynnikowymi i zdaniowymi, które dziś dominują. Widzimy przykłady systemów planowania portfela, w których dostępny jest zbiór algorytmów, które można zastosować do dowolnego problemu. Można to zrobić selektywnie (system klasyfikuje każdy nowy problem, aby wybrać najlepszy dla niego algorytm) lub równolegle (wszystkie algorytmy działają jednocześnie, każdy na innym procesorze) lub przeplatając algorytmy zgodnie z harmonogramem.

Zaczynamy od rozważenia tylko problemu harmonogramowania czasowego, ignorując ograniczenia zasobów. Aby zminimalizować makepan (czas trwania planu), musimy znaleźć najwcześniejsze czasy rozpoczęcia dla wszystkich działań zgodnych z ograniczeniami porządkowania dostarczonymi z problemem. Pomocne jest przeglądanie tych ograniczeń porządkowania jako ukierunkowanego wykresu związanego z działaniami, jak pokazano.

Do tego wykresu możemy zastosować metodę ścieżki krytycznej (CPM), aby określić możliwe czasy rozpoczęcia i zakończenia każdego działania. Ścieżka przez wykres przedstawiający plan częściowego zamówienia to liniowo uporządkowana sekwencja działań rozpoczynająca się od Start i kończąca się na Zakończ. (Na przykład w planie częściowego zamówienia na rysunku znajdują się dwie ścieżki.

Ścieżka krytyczna to ścieżka, której całkowity czas trwania jest najdłuższy; ścieżka jest „krytyczna”, ponieważ determinuje czas trwania całego planu – skrócenie innych ścieżek nie skraca planu jako całości, ale opóźnienie rozpoczęcia jakichkolwiek działań na ścieżce krytycznej spowalnia cały plan. Akcje, które znajdują się poza ścieżką krytyczną, mają określony czas, w którym można je wykonać. Okno jest określone jako najwcześniejszy możliwy czas rozpoczęcia, ES , i najpóźniejszy możliwy czas rozpoczęcia, LS . Wielkość LS – ES nazywana jest luzem akcji. Na rysunku powyżej widać, że cały plan zajmie 85 minut, że każda akcja w najwyższym zadaniu ma 15 minut przerwy i że każda akcja na ścieżce krytycznej nie ma luzu (z definicji). Razem czasy ES i LS dla wszystkich działań stanowią harmonogram dla problemu. Poniższe wzory definiują ES i LS i stanowią algorytm programowania dynamicznego do ich obliczania. A i B są akcjami a oznacza, że  A poprzedza B:

Pomysł polega na tym, że zaczynamy od przypisania ES(Start) do wartości 0. Następnie, gdy tylko otrzymamy akcję B taką, że wszystkie akcje, które pojawiają się bezpośrednio przed B, mają przypisane wartości ES, ustawiamy ES(B) jako maksimum najwcześniejszych czasów zakończenia tych bezpośrednio poprzedzających akcji, gdzie najwcześniejszy czas zakończenia akcji jest zdefiniowany jako najwcześniejszy czas rozpoczęcia plus czas trwania. Ten proces powtarza się, dopóki każdej akcji nie zostanie przypisana wartość ES. Wartości LS są obliczane w podobny sposób, działając wstecz od akcji Zakończ. Złożoność algorytmu ścieżki krytycznej wynosi po prostu O(Nb), gdzie N jest liczbą działań, a b jest maksymalnym współczynnikiem rozgałęzienia do lub z działania. (Aby to zobaczyć, zauważ, że obliczenia LS i ES są wykonywane raz dla każdego działania, a każde obliczenie wykonuje iterację po co najmniej b innych działaniach). Dlatego znalezienie harmonogramu o minimalnym czasie trwania, biorąc pod uwagę częściową kolejność działań i brak zasobów ograniczenia, jest dość łatwe. Mówiąc matematycznie, problemy ścieżki krytycznej są łatwe do rozwiązania, ponieważ są definiowane jako połączenie liniowych nierówności w czasie początkowym i końcowym. Kiedy wprowadzamy ograniczenia zasobów, wynikające z tego ograniczenia dotyczące czasu rozpoczęcia i zakończenia stają się bardziej skomplikowane. Na przykład akcje AddEngine, które rozpoczynają się w tym samym czasie na rysunku powyżej, wymagają tego samego EngineHoist i nie mogą się nakładać. Ograniczenie „nie może się nakładać” to alternatywa dwóch nierówności liniowych, po jednej dla każdego możliwego uporządkowania. Okazuje się, że wprowadzenie rozłączeń powoduje, że planowanie z ograniczeniami zasobów NPhard. Rysunek pokazuje rozwiązanie z najszybszym czasem realizacji, 115 minut.

To o 30 minut dłużej niż 85 minut wymagane dla harmonogramu bez ograniczeń zasobów. Zauważ, że nie ma czasu, w którym obaj inspektorzy są potrzebni, więc możemy natychmiast przenieść jednego z naszych dwóch inspektorów na bardziej produktywną pozycję.

Praca nad optymalnym harmonogramowaniem ma długą historię. Wyzwanie postawione w 1963 r. — aby znaleźć optymalny harmonogram dla problemu obejmującego zaledwie 10 maszyn i 10 zadań po 100 czynności każde — pozostawał nierozwiązany przez 23 lata . Wypróbowano wiele podejść, w tym rozgałęzione, symulowane wyżarzanie, przeszukiwanie tabu i spełnianie ograniczeń. Jednym z popularnych podejść jest heurystyka minimalnego luzu: w każdej iteracji należy zaplanować najwcześniejszy możliwy start, bez względu na to, które nieplanowane działanie ma zaplanowane wszystkie poprzednie i ma najmniej luzu; następnie zaktualizuj czasy ES i LS dla każdego działania, którego dotyczy problem, i powtórz. Ta zachłanna heurystyka przypomina heurystykę minimalnych pozostałych wartości (MRV) w spełnianiu ograniczeń. Często działa dobrze w praktyce, ale dla naszego problemu z montażem daje 130-minutowe rozwiązanie, a nie 115-minutowe rozwiązanie z powyższego rysunku. Do tego momentu zakładaliśmy, że zestaw akcji i ograniczeń porządkowych jest stały. Zgodnie z tymi założeniami każdy problem związany z planowaniem można rozwiązać za pomocą nienakładającej się sekwencji, która pozwala uniknąć wszelkich konfliktów zasobów, pod warunkiem, że każde działanie jest samo w sobie wykonalne. Jeśli jednak problem z planowaniem okazuje się bardzo trudny, rozwiązanie go w ten sposób może nie być dobrym pomysłem – może lepiej przemyśleć działania i ograniczenia, na wypadek gdyby prowadziło to do znacznie łatwiejszego problemu z planowaniem. Dlatego warto zintegrować planowanie i harmonogramowanie, biorąc pod uwagę czasy trwania i nakładanie się podczas konstruowania planu. Kilka algorytmów planowania można rozszerzyć, aby obsłużyć te informacje.

Typowy problem z planowaniem warsztatów składa się ze zbioru zadań, z których każde zawiera zbiór akcji z ograniczeniami kolejności. Każda akcja ma czas trwania i zestaw ograniczeń zasobów wymaganych przez akcję. Ograniczenie określa typ zasobu (np. śruby, klucze lub piloty), liczbę wymaganych zasobów oraz to, czy zasób nadaje się do użytku (np. śruby nie są już dostępne do użytku) czy wielokrotnego użytku (np. pilot jest zajęty podczas lotu, ale jest ponownie dostępny po zakończeniu lotu). Akcje mogą również produkować zasoby (np. akcje produkcji i zaopatrzenia). Rozwiązanie problemu z harmonogramem warsztatów określa czas rozpoczęcia każdego działania i musi spełniać wszystkie ograniczenia porządku czasowego i ograniczenia zasobów. Podobnie jak w przypadku problemów związanych z wyszukiwaniem i planowaniem, rozwiązania można oceniać według funkcji kosztu; może to być dość skomplikowane, z nieliniowymi kosztami zasobów, zależnymi od czasu kosztami opóźnień i tak dalej. Dla uproszczenia zakładamy, że funkcja kosztu to po prostu całkowity czas trwania planu, który nazywa się makespan. Poniżej pokazuje prosty przykład: problem związany z montażem dwóch samochodów. Problem składa się z dwóch zadań, każde w formie [AddEngine,AddWheels, Inspect]. Następnie oświadczenie Resources deklaruje, że istnieją cztery rodzaje zasobów i podaje liczbę każdego typu dostępnego na początku: 1 wciągnik silnikowy, 1 stacja kołowa, 2 inspektorów i 500 nakrętek. Schematy akcji podają czas trwania i zapotrzebowanie na zasoby każdej akcji. Nakrętki są zużywane, gdy koła są dodawane do samochodu, podczas gdy inne zasoby są „pożyczane” na początku akcji i uwalniane pod koniec akcji.

Reprezentacja zasobów jako ilości liczbowych, takich jak Inspectors(2), a nie jako nazwane jednostki, takie jak Inspector(I₁) i Inspector(I₂) , jest przykładem techniki zwanej agregacją: grupowanie pojedynczych obiektów w ilości, gdy wszystkie obiekty są nie do odróżnienia. W naszym problemie montażowym nie ma znaczenia, który inspektor sprawdza samochód, więc nie ma potrzeby robienia rozróżnienia. Agregacja jest niezbędna do zmniejszenia złożoności. Zastanów się, co się stanie, gdy proponowany harmonogram obejmuje 10 jednoczesnych działań kontrolnych, ale dostępnych jest tylko 9 inspektorów. Gdy inspektorzy są reprezentowani jako ilości, awaria jest wykrywana natychmiast, a algorytm cofa się, aby wypróbować inny harmonogram. W przypadku inspektorów reprezentowanych jako osoby, algorytm wypróbowałby wszystkie 9! sposoby przypisywania inspektorów do działań, zanim zauważą, że żaden z nich nie działa.

Klasyczne planowanie mówi o tym, co robić, w jakiej kolejności, ale nie mówi o czasie: jak długo trwa akcja i kiedy ma miejsce. Na przykład w domenie lotnisk moglibyśmy stworzyć plan mówiący, które samoloty dokąd lecą, przewożąc co, ale nie moglibyśmy określić czasu odlotu i przylotu. To jest przedmiot planowania. Rzeczywisty świat narzuca również ograniczenia zasobów: linia lotnicza ma ograniczoną liczbę pracowników, a pracownicy jednego lotu nie mogą być w tym samym czasie na drugim. W tej sekcji przedstawiono techniki planowania i harmonogramowania problemów z ograniczeniami zasobów. Podejście, które przyjmujemy, to „najpierw zaplanuj, zaplanuj później”: podziel ogólny problem na fazę planowania, w której wybierane są działania, z pewnymi ograniczeniami porządkowymi, aby osiągnąć cele problemu, oraz na późniejszą fazę planowania, w której informacje czasowe jest dodawany do planu, aby upewnić się, że spełnia on ograniczenia dotyczące zasobów i terminów. Takie podejście jest powszechne w rzeczywistych warunkach produkcyjnych i logistycznych, gdzie faza planowania jest czasami zautomatyzowana, a czasami wykonywana przez ekspertów.

Wyobraź sobie robota do zgrzewania punktowego w fabryce samochodów. Szybkie, dokładne ruchy robota są powtarzane w kółko, gdy każdy samochód przejeżdża wzdłuż linii. Choć technicznie imponujący, robot prawdopodobnie wcale nie wydaje się inteligentny, ponieważ ruch jest stałą, zaprogramowaną sekwencją; robot oczywiście nie „wie, co robi” w żadnym sensownym sensie. Załóżmy teraz, że źle przymocowane drzwi spadają z samochodu w chwili, gdy robot ma zamiar zastosować zgrzewanie punktowe. Robot szybko zastępuje siłownik spawalniczy chwytakiem, podnosi drzwi, sprawdza je pod kątem zarysowań, ponownie przyczepia je do samochodu, wysyła e-mail do nadzorcy hali, przełącza się z powrotem na siłownik spawalniczy i wznawia pracę. Nagle zachowanie robota wydaje się celowe, a nie rutynowe; zakładamy, że nie wynika to z rozległego, wstępnie obliczonego planu warunkowego, ale z procesu ponownego planowania online – co oznacza, że ​​robot musi wiedzieć, co próbuje zrobić. Ponowne planowanie zakłada pewną formę monitorowania wykonania w celu określenia potrzeby nowego planu. Jedna z takich potrzeb pojawia się, gdy agent planowania warunkowego zmęczy się planowaniem każdego najmniejszego zdarzenia, na przykład tego, czy niebo może spaść mu na głowę. Oznacza to, że plan warunkowy pozostaje w formie niekompletnej. Na przykład, niektóre gałęzie częściowo zbudowanego planu warunkowego mogą po prostu powiedzieć Replan; jeśli taka gałąź zostanie osiągnięta podczas wykonywania, agent powraca do trybu planowania. Jak wspomnieliśmy wcześniej, decyzja o tym, ile problemu rozwiązać wcześniej, a ile pozostawić do przeplanowania, to decyzja, która wiąże się z kompromisami między możliwymi zdarzeniami o różnych kosztach i prawdopodobieństwie wystąpienia. Nikt nie chce zepsuć samochodu na środku Sahary i dopiero wtedy pomyśleć o wystarczającej ilości wody. Ponowne planowanie może być konieczne, jeśli model świata agenta jest błędny. Model działania może mieć brakujący warunek wstępny — na przykład agent może nie wiedzieć, że zdjęcie wieczka puszki z farbą często wymaga śrubokręta. Model może mieć brakujący efekt — pomalowanie przedmiotu może również spowodować zabrudzenie podłogi. Lub model może mieć brakujący bieg, który jest po prostu nieobecny w reprezentacji — na przykład model podany wcześniej nie ma pojęcia o ilości farby w puszce, o tym, jak jej działania wpływają na tę ilość, ani o potrzebie kwota niezerowa. Model może również nie uwzględniać zdarzeń egzogenicznych, takich jak ktoś przewracający puszkę z farbą. Zdarzenia egzogeniczne mogą również obejmować zmiany celu, takie jak dodanie wymogu, aby stół i krzesło nie były pomalowane na czarno. Bez możliwości monitorowania i ponownego planowania zachowanie agenta może być kruche, jeśli opiera się na absolutnej poprawności swojego modelu.

Agent online ma do wyboru (co najmniej) trzy różne podejścia do monitorowania środowiska podczas wykonywania planu:

MONITOROWANIE AKCJI: przed wykonaniem akcji agent sprawdza, czy wszystkie warunki wstępne są nadal spełnione.

MONITOROWANIE PLANU: przed wykonaniem akcji agent sprawdza, czy pozostały plan nadal się powiedzie.

MONITOROWANIE CELÓW: przed wykonaniem działania agent sprawdza, czy istnieje lepszy zestaw celów, które mógłby osiągnąć.

Na rysunku widzimy schemat monitorowania działań. Agent śledzi zarówno swój pierwotny plan, cały plan, jak i część planu, która nie została jeszcze zrealizowana, co oznacza plan. Po wykonaniu kilku pierwszych kroków planu agent oczekuje, że znajdzie się w stanie E . Ale agent zauważa, że faktycznie jest w stanie O . Następnie musi naprawić plan, znajdując jakiś punkt P na pierwotnym planie, do którego może wrócić. (Być może P jest stanem docelowym G, .) Agent stara się zminimalizować całkowity koszt planu: część naprawczą (od O do P ) plus kontynuację (od P do G).

Wróćmy teraz do przykładowego problemu uzyskania krzesła i stołu w dopasowanym kolorze. Załóżmy, że agent wymyśli taki plan:

Teraz agent jest gotowy do wykonania planu. Agent zauważa, że stół i puszka farby są białe, a krzesło czarne. Następnie wykonuje 

W tym momencie klasyczny planista ogłosi zwycięstwo; plan został wykonany. Ale agent monitorowania wykonywania w trybie online musi sprawdzić, czy akcja się powiodła. Załóżmy, że agent dostrzega, że ​​krzesło jest nakrapiane szare, ponieważ prześwituje czarna farba. Następnie agent musi określić pozycję odzyskiwania w planie, do której ma dążyć, oraz sekwencję działań naprawczych, aby tam dotrzeć. Agent zauważa, że ​​bieżący stan jest identyczny z warunkiem wstępnym przed akcją więc wybiera pustą sekwencję do naprawy i ustawia swój plan jako taką samą sekwencję [Paint], którą właśnie próbował. Po wdrożeniu nowego planu monitorowanie wykonania jest wznawiane, a akcja Malowanie jest ponawiana. To zachowanie będzie się powtarzać, dopóki krzesło nie będzie postrzegane jako całkowicie pomalowane. Ale zauważ, że pętla jest tworzona przez proces planu-wykonaj-przeplanuj, a nie przez wyraźną pętlę w planie. Należy również zauważyć, że pierwotny plan nie musi obejmować wszystkich nieprzewidzianych okoliczności. Jeśli agent osiągnie krok oznaczony REPLAN, może wygenerować nowy plan (być może z udziałem Can2). Monitorowanie akcji to prosta metoda monitorowania wykonania, ale czasami może prowadzić do mniej niż inteligentnego zachowania. Załóżmy na przykład, że nie ma czarnej ani białej farby, a agent opracowuje plan rozwiązania problemu z malowaniem, malując zarówno krzesło, jak i stół na czerwono. Załóżmy, że na krzesło wystarczy tylko czerwonej farby. Dzięki monitorowaniu działań agent pomalowałby krzesło na czerwono, a następnie zauważyłby, że nie ma w nim farby i nie może pomalować stołu, po czym przeplanowałby naprawę – być może pomalował zarówno krzesło, jak i stół na zielono. Agent monitorowania planu może wykryć niepowodzenie, gdy obecny stan jest taki, że pozostały plan już nie działa. W ten sposób nie tracił czasu na malowanie krzesła na czerwono. Monitorowanie planu osiąga to poprzez sprawdzenie warunków wstępnych powodzenia całego pozostałego planu, to znaczy warunków wstępnych każdego etapu planu, z wyjątkiem warunków wstępnych, które zostały osiągnięte przez inny krok w pozostałym planie. Monitorowanie planu odcina wykonanie skazanego planu tak szybko, jak to możliwe, zamiast kontynuować aż do faktycznego wystąpienia awarii. Monitorowanie planu pozwala również na zbieg okoliczności – przypadkowy sukces. Jeśli ktoś przyjdzie i pomaluje stół na czerwono w tym samym czasie, gdy agent maluje na czerwono krzesło, to ostateczne warunki planu są spełnione (cel został osiągnięty) i agent może wcześniej wrócić do domu. Modyfikowanie algorytmu planowania w taki sposób, aby każde działanie w planie było opatrzone adnotacjami z warunkami wstępnymi działania, jest proste, umożliwiając w ten sposób monitorowanie działań. Nieco bardziej skomplikowane jest umożliwienie monitorowania planu. Planiści częściowego porządku mają tę zaletę, że zbudowali już struktury, które zawierają relacje niezbędne do monitorowania planu. Wzbogacanie planistów przestrzeni stanowej o niezbędne adnotacje można wykonać poprzez staranne prowadzenie ksiąg rachunkowych, ponieważ osoby biegle osiągające cele są cofane przez plan. Teraz, gdy opisaliśmy już metodę monitorowania i ponownego planowania, musimy zapytać: „Czy to działa?” To zaskakująco trudne pytanie. Jeśli mamy na myśli: „Czy możemy zagwarantować, że agent zawsze osiągnie cel?” wtedy odpowiedź brzmi nie, ponieważ agent może nieumyślnie dojść do ślepego zaułka, z którego nie ma naprawy. Na przykład odkurzacz może mieć wadliwy model samego siebie i nie wiedzieć, że jego baterie mogą się wyczerpać. Kiedy to zrobią, nie naprawią żadnych planów. Jeśli wykluczymy ślepe uliczki – załóżmy, że istnieje plan osiągnięcia celu z dowolnego stanu w środowisku – i załóżmy, że środowisko jest naprawdę niedeterministyczne, w tym sensie, że taki plan zawsze ma jakieś szanse powodzenia w danej realizacji próba, wtedy agent w końcu osiągnie cel. Problem pojawia się, gdy pozornie niedeterministyczne działanie nie jest w rzeczywistości przypadkowe, ale raczej zależy od jakiegoś warunku, o którym agent nie wie. Na przykład czasami puszka po farbie może być pusta, więc malowanie z niej może nie przynosić efektu. Żadna ilość ponownych prób tego nie zmieni. Jednym z rozwiązań jest losowy wybór z zestawu możliwych planów naprawczych, zamiast próbować za każdym razem tego samego. W takim przypadku plan naprawy otwarcia kolejnej puszki może zadziałać. Lepszym podejściem jest nauczenie się lepszego modelu. Każde niepowodzenie przewidywania jest okazją do nauki; podmiot powinien być w stanie modyfikować swój model świata, aby był zgodny z jego percepcjami. Od tego momentu osoba zajmująca się ponownym planowaniem będzie mogła wymyślić naprawę, która dotrze do źródła problemu, zamiast polegać na szczęściu w wyborze dobrej naprawy.

Widzieliśmy, że planowanie awaryjne – generowanie planów z warunkowym rozgałęzieniem w oparciu o spostrzeżenia – jest odpowiednie dla środowisk z częściową obserwowalnością, niedeterminizmem lub jednym i drugim. Dla częściowo obserwowalnego problemu malowania z podanymi wcześniej schematami percepcji, jedno z możliwych warunkowych rozwiązań jest następujące:

Zmienne w tym planie należy uznać za egzystencjalnie skwantyfikowane; druga linia mówi, że jeśli istnieje jakiś kolor, czyli kolor stołu i krzesła, to agent nie musi nic robić, aby osiągnąć cel. Wykonując ten plan, agent planowania warunkowego może zachować swój stan przekonań jako logiczną formułę i ocenić każdy warunek gałęzi, określając, czy stan przekonania pociąga za sobą formułę warunku, czy jego negację. (Do algorytmu planowania warunkowego należy upewnienie się, że agent nigdy nie znajdzie się w stanie przekonania, w którym wartość prawdy formuły warunku jest nieznana). Należy zauważyć, że w przypadku warunków pierwszego rzędu formuła może być spełniona w więcej niż jednokierunkowa; na przykład warunek może być spełniony przez i przez jeśli obie puszki są tego samego koloru co stół. W takim przypadku agent może wybrać dowolne satysfakcjonujące zastąpienie, aby zastosować się do reszty planu. Jak pokazano wcześniej, obliczanie nowego stanu przekonań po działaniu i następującym po nim spostrzeżeniu odbywa się w dwóch etapach. Pierwszy etap oblicza stan przekonania po działaniu, tak jak w przypadku agenta bezczujnikowego:

gdzie, jak poprzednio, przyjęliśmy stan wiary reprezentowany jako koniunkcja dosłownych. Drugi etap jest nieco trudniejszy. Załóżmy, że otrzymano literały perceptu p1…,pk. Można by pomyśleć, że po prostu musimy je dodać do stanu wiary; w rzeczywistości możemy również wywnioskować, że warunki wstępne wykrywania są spełnione. Teraz, jeśli percept p ma dokładnie jeden schemat percepcji,  , gdzie c jest koniunkcją literałów, to te literały mogą zostać wprowadzone do stanu przekonania razem z p . Z drugiej strony, jeśli p ma więcej niż jeden schemat percepcji, którego warunki wstępne mogą obowiązywać zgodnie z przewidywanym stanem przekonania b , wtedy musimy dodać alternatywę warunków wstępnych. Oczywiście prowadzi to do stanu przekonania poza 1-CNF i wywołuje te same komplikacje, co efekty warunkowe, z bardzo tymi samymi klasami rozwiązań. Dysponując mechanizmem obliczania dokładnych lub przybliżonych stanów przekonań, możemy generować plany warunkowe z rozszerzeniem wyszukiwania do przodu AND–OR względem stosowanych wcześniej stanów przekonań. Akcje z niedeterministycznymi efektami — które są definiowane po prostu za pomocą alternatywy w EFEKCIE schematu działania — mogą być uwzględnione z niewielkimi zmianami w obliczeniach aktualizacji stanu przekonań i bez zmian w algorytmie wyszukiwania. W przypadku funkcji heurystycznej wiele metod sugerowanych dla planowania bezczujnikowego ma również zastosowanie w przypadku częściowo obserwowalnym, niedeterministycznym.

Wcześniej wprowadziliśmy podstawową ideę poszukiwania w przestrzeni stanów przekonań, aby znaleźć rozwiązanie problemów bezczujnikowych. Zakładamy, że podstawowy problem planowania jest deterministyczny. Początkowy stan przekonania dotyczący problemu z malowaniem bezczujnikowym może zignorować płynność InView, ponieważ agent nie ma czujników. Ponadto przyjmujemy za niezmienne fakty ponieważ obowiązują one w każdym stanie wiary. Agent nie zna kolorów puszek lub przedmiotów, ani tego, czy puszki są otwarte, czy zamknięte, ale wie, że przedmioty i puszki mają kolory  Po Skolemizing otrzymujemy początkowy stan wiary:

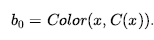
W planowaniu klasycznym, w którym przyjmuje się założenie o zamkniętym świecie, przyjęlibyśmy, że każdy płyn nie wymieniony w stanie jest fałszywy, ale w planowaniu bezczujnikowym (i częściowo obserwowalnym) musimy przełączyć się na założenie otwartego świata, w którym stany zawierają zarówno biegły pozytywny, jak i negatywny, a jeśli biegły się nie pojawia, jego wartość jest nieznana. Zatem stan przekonań odpowiada dokładnie zbiorowi możliwych światów, które spełniają formułę. Biorąc pod uwagę ten początkowy stan przekonań, następująca sekwencja działań jest rozwiązaniem:

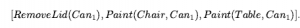
Pokażemy teraz, jak rozwinąć stan przekonań poprzez sekwencję działań, aby pokazać, że ostateczny stan przekonań spełnia cel. Po pierwsze, zauważ, że w danym stanie przekonania b , podmiot może rozważyć każde działanie, którego warunki wstępne są spełnione przez b . (Innych działań nie można użyć, ponieważ model przejścia nie definiuje skutków działań, których warunki wstępne mogą być niespełnione). Ogólna formuła aktualizacji stanu przekonania b przy odpowiednim działaniu w deterministycznym świecie jest następująca:

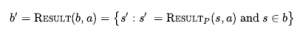
gdzie RESULT_P definiuje fizyczny model przejścia. Na razie zakładamy, że początkowy stan wiary jest zawsze koniunkcją literałów, czyli formułą 1-CNF. Aby skonstruować nowy stan przekonań b’ , musimy rozważyć, co dzieje się z każdym dosłownym l w każdym stanie fizycznym s w b, gdy stosowane jest działanie a. W przypadku literałów, których wartość logiczna jest już znana w b , wartość logiczna w b’ jest obliczana na podstawie wartości bieżącej oraz listy add i delete akcji. (Na przykład, jeśli l znajduje się na liście usuwania akcji, to ¬l jest dodawany  b’) A co z literałem a , którego wartość prawdy jest nieznana w b? Istnieją trzy przypadki:

1. Jeśli akcja dodaje l , to l będzie prawdziwe w b’ niezależnie od jego wartości początkowej.
2. Jeśli akcja usunie l , to l będzie fałszywe w b’ niezależnie od jego wartości początkowej.
3. Jeśli akcja nie wpływa na l , to l zachowa swoją początkową wartość (która jest nieznana) i nie pojawi się w b’ .

Widzimy więc, że obliczenie b’ jest prawie identyczne z obserwowalnym przypadkiem.

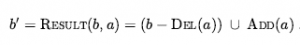
Nie możemy całkowicie użyć semantyki zbiorów, ponieważ (1) musimy upewnić się, że b’ nie zawiera zarówno l, jak i ¬l oraz (2) atomy mogą zawierać niezwiązane zmienne. Ale nadal tak jest że RESULT_P(b,a) jest obliczany zaczynając od b , ustawiając każdy atom, który pojawia się w Del(a) na false i ustawiając każdy atom, który pojawia się w ADD(a) na true. Na przykład, jeśli zastosujemy RemoveLid(Can₁) do początkowego stanu przekonania b₀ , otrzymamy

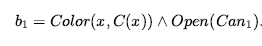
Kiedy wykonujemy akcję   ,warunek jest spełniony przez dosłowne z wiązaniem i nowym stanem wiary jest 

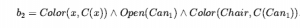
Na koniec stosujemy akcję aby uzyskać

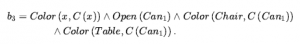
Ostateczny stan przekonania spełnia cel  ze  zmienną c przywiązaną do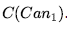

Poprzednia analiza reguły aktualizacji wykazała bardzo ważny fakt: rodzina stanów przekonań definiowanych jako koniunkcje literałów jest zamknięta pod aktualizacjami zdefiniowanymi przez schematy działania PDDL. Oznacza to, że jeśli stan przekonania zaczyna się jako koniunkcja literałów, to każda aktualizacja da koniunkcję literałów. Oznacza to, że w świecie z n biegłościami każdy stan przekonań może być reprezentowany przez koniunkcję rozmiaru O(n) . To bardzo pocieszający wynik, biorąc pod uwagę, że na świecie jest 2ⁿ stanów. Mówi, że możemy zwięźle przedstawić wszystkie podzbiory tych 2ⁿ stanów, których kiedykolwiek będziemy potrzebować. Co więcej, proces sprawdzania stanów przekonań, które są podzbiorami lub nadzbiorami wcześniej odwiedzonych stanów przekonań, jest również łatwy, przynajmniej w przypadku zdań. Istotą tego przyjemnego obrazu jest to, że działa on tylko w przypadku schematów działania, które mają takie same skutki dla wszystkich stanów, w których spełnione są ich warunki wstępne. To właśnie ta właściwość umożliwia zachowanie reprezentacji stanu przekonań 1-CNF. Gdy tylko efekt może zależeć od stanu, wprowadzane są zależności między biegłymi, a właściwość 1-CNF zostaje utracona. Rozważmy na przykład prosty świat próżni zdefiniowany wcześniej. Niech biegły to AtL i AtR dla lokalizacji robota oraz CleanL i CleanR dla stanu kwadratów. Zgodnie z definicją problemu działanie Ssania nie ma żadnego warunku wstępnego – zawsze można to zrobić. Trudność polega na tym, że jego efekt zależy od lokalizacji robota: gdy robot jest AtL, wynikiem jest CleanL, ale gdy jest AtR, wynikiem jest CleanR. W przypadku takich działań nasze schematy działania będą potrzebowały czegoś nowego: efektu warunkowego. Mają one składnię „gdy warunek: efekt”, gdzie warunek jest logiczną formułą porównywaną z bieżącym stanem, a efekt jest formułą opisującą stan wynikowy. Dla świata próżni:

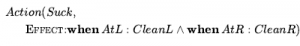
Po zastosowaniu do początkowego stanu przekonania True, wynikowym stanem przekonania jest  który nie jest już w 1-CNF. Ogólnie, efekty warunkowe mogą wywoływać arbitralne zależności między osobami biegłymi w stanie przekonań, prowadząc w najgorszym przypadku do stanów przekonań o wielkości wykładniczej. Ważne jest, aby zrozumieć różnicę między warunkami wstępnymi a efektami warunkowymi. Wszystkie efekty warunkowe, których warunki są spełnione, mają swoje efekty stosowane w celu wygenerowania wynikowego stanu przekonania; jeśli żaden nie jest spełniony, stan wynikowy pozostaje niezmieniony. Z drugiej strony, jeśli warunek wstępny nie jest spełniony, to akcja nie ma zastosowania, a stan wynikowy jest nieokreślony. Z punktu widzenia planowania bezczujnikowego lepiej jest mieć efekty warunkowe niż działanie nie dające się zastosować. Na przykład możemy podzielić Ssanie na dwie akcje z bezwarunkowymi skutkami w następujący sposób:

Teraz mamy tylko schematy bezwarunkowe, więc wszystkie stany przekonań pozostają w 1-CNF; niestety nie możemy określić stosowalności SuckL i SuckR w początkowym stanie wiary. Wydaje się zatem nieuniknione, że nietrywialne problemy będą obejmować niestabilne stany przekonań, podobnie jak te, które napotkaliśmy, gdy rozważaliśmy problem szacowania stanu dla świata wumpusów. Sugerowanym wówczas rozwiązaniem było użycie konserwatywnego przybliżenia do dokładnego stanu przekonań; na przykład stan przekonania może pozostać w 1-CNF, jeśli zawiera wszystkie literały, których wartości prawdy można określić i traktuje wszystkie inne literały jako nieznane. Chociaż to podejście jest słuszne, ponieważ nigdy nie generuje błędnego planu, jest niekompletne, ponieważ może nie być w stanie znaleźć rozwiązań problemów, które z konieczności wiążą się z interakcjami między literałami. Aby dać trywialny przykład, jeśli celem jest, aby robot znalazł się na czystym kwadracie, to [Ssanie] jest rozwiązaniem, ale agent bezczujnikowy, który nalega na stany przekonań 1-CNF, nie znajdzie go. Być może lepszym rozwiązaniem jest szukanie sekwencji działań, które utrzymają stan przekonań tak prosty, jak to tylko możliwe. W świecie próżni bezczujnikowej sekwencja działań [Prawo,Ssanie,Lewo,Ssanie] generuje następującą sekwencję stanów przekonań:

Oznacza to, że agent może rozwiązać problem, zachowując stan przekonania 1-CNF, nawet jeśli niektóre sekwencje (np. te zaczynające się od Suck) wychodzą poza 1-CNF. Ogólna lekcja nie jest stracona dla ludzi: zawsze wykonujemy drobne czynności (sprawdzamy czas, klepiemy po kieszeniach, aby upewnić się, że mamy kluczyki do samochodu, czytamy znaki drogowe podczas poruszania się po mieście), aby wyeliminować niepewność i zachować nasze przekonania do opanowania. Jest jeszcze inne, zupełnie inne podejście do problemu nieporadnie poruszających się stanów wiary: w ogóle nie zawracaj sobie głowy ich obliczaniem. Załóżmy, że początkowy stan przekonań b0 jest i chcielibyśmy poznać stan przekonań wynikający z sekwencji działania [a₁…a_m] . Zamiast obliczać to wprost, po prostu przedstaw to jako „b0, a następnie [a₁…a_m]”. Jest to leniwa, ale jednoznaczna reprezentacja stanu przekonań i jest dość zwięzła — O(n+m), gdzie n jest rozmiarem początkowego stanu przekonań (zakłada się, że jest w 1-CNF), a m jest maksymalną długością sekwencja działań. Jako reprezentacja stanu przekonań ma jednak jedną wadę: ustalenie, czy cel jest spełniony, czy działanie jest możliwe, może wymagać wielu obliczeń. Obliczenie można zaimplementować jako test implikacji: jeśli A_m reprezentuje zbiór aksjomatów stanu następcy wymaganych do zdefiniowania wystąpień akcji a₁ .. a_m — jak wyjaśniono dla SATPLAN — a G_m zapewnia, że ​​cel jest prawdziwy po m krokach, to plan osiąga cel, jeśli — to znaczy, jeśli  jest niezadowalające.

Biorąc pod uwagę nowoczesny solver SAT, może być możliwe zrobienie tego znacznie szybciej niż obliczenie pełnego stanu wiary. Na przykład, jeśli żadne z działań w sekwencji nie ma określonego celu płynnego na swojej liście dodawania, solver wykryje to natychmiast. Pomocne jest również, jeśli częściowe wyniki dotyczące stanu przekonań — na przykład biegły, o którym wiadomo, że są prawdziwe lub fałszywe — są zapisywane w pamięci podręcznej, aby uprościć kolejne obliczenia. Ostatnim elementem układanki planowania bezczujnikowego jest funkcja heurystyczna, która kieruje poszukiwaniami. Znaczenie funkcji heurystycznej jest takie samo jak w przypadku planowania klasycznego: oszacowanie (być może dopuszczalne) kosztu osiągnięcia celu z danego stanu wiary. W przypadku stanów przekonań mamy jeden dodatkowy fakt: rozwiązanie dowolnego podzbioru stanu przekonań jest z konieczności łatwiejsze niż rozwiązanie stanu przekonań: stąd każda dopuszczalna heurystyka obliczona dla podzbioru jest dopuszczalna dla samego stanu przekonań. Najbardziej oczywistymi kandydatami są podzbiory singletonów, czyli poszczególne stany fizyczne.

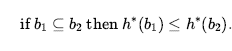
Stąd każda dopuszczalna heurystyka obliczona dla podzbioru jest dopuszczalna dla samego stanu przekonań. Najbardziej oczywistymi kandydatami są podzbiory singletonów, czyli poszczególne stany fizyczne. Możemy wziąć dowolny losowy zbiór stanów s₁, … s_N, które są w stanie przekonania b , zastosować dowolną dopuszczalną heurystykę h i zwrócić

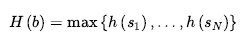
jako oszacowanie heurystyczne do rozwiązania. Możemy również użyć niedopuszczalnych heurystyk, takich jak heurystyka „ignoruj-usuń-listy”, która wydaje się działać całkiem dobrze w praktyce.