Miesiąc: marzec 2022

Widzieliśmy, że reguła Bayesa może być przydatna do odpowiadania na pytania probabilistyczne uwarunkowane jednym dowodem – na przykład sztywnością karku. W szczególności argumentowaliśmy, że informacja probabilistyczna jest często dostępna w postaci P(efekt | przyczyna) . Co się dzieje, gdy mamy dwa lub więcej dowodów? Na przykład, co może wyciągnąć dentysta, jeśli jej paskudna stalowa sonda zaczepi się o bolący ząb pacjenta? Jeśli znamy pełny rozkład łączny , możemy odczytać odpowiedź:

Wiemy jednak, że takie podejście nie skaluje się do większej liczby zmiennych. Możemy spróbować użyć reguły Bayesa do przeformułowania problemu:

Aby to przeformułowanie zadziałało, musimy znać prawdopodobieństwa warunkowe połączenia tothache Λ catch  dla każdej wartości Cavity . Może to być wykonalne dla zaledwie dwóch zmiennych dowodowych, ale znowu nie zwiększa się. Jeśli istnieje n możliwych zmiennych dowodowych (prześwietlenia, dieta, higiena jamy ustnej itp.), to istnieje O(2ⁿ) możliwych kombinacji obserwowanych wartości, dla których musielibyśmy znać prawdopodobieństwa warunkowe. Nie jest to lepsze niż korzystanie z pełnej dystrybucji łącznej. Aby zrobić postęp, musimy znaleźć dodatkowe twierdzenia dotyczące dziedziny, które pozwolą nam uprościć wyrażenia. Pojęcie niezależności dostarcza wskazówki, ale wymaga doprecyzowania. Byłoby miło, gdyby Toothach i Catch były niezależne, ale nie są: jeśli sonda zaczepi się o ząb, to prawdopodobnie ząb ma ubytek i ubytek powoduje ból zęba. Zmienne te są jednak niezależne, biorąc pod uwagę obecność lub brak wnęki. Każda z nich jest bezpośrednio spowodowana ubytkiem, ale żadna nie ma bezpośredniego wpływu na drugą: ból zęba zależy od stanu nerwów w zębie, natomiast dokładność sondy zależy przede wszystkim od umiejętności dentysty, dla którego ból zęba jest nieistotny. Matematycznie ta właściwość jest zapisana jako

Równanie to wyraża warunkową niezależność toothache i catch daego Cavity. Możemy to wstawić do równania, aby uzyskać prawdopodobieństwo Cavity:

Teraz wymagania informacyjne są takie same, jak w przypadku wnioskowania, przy czym każdy dowód jest używany oddzielnie: prawdopodobieństwo a priori P(Cavity) dla zmiennej zapytania oraz prawdopodobieństwo warunkowe każdego efektu, biorąc pod uwagę jego przyczynę. Ogólna definicja warunkowej niezależności dwóch zmiennych X i Y , przy danej trzeciej zmiennej Z, to

Na przykład w dziedzinie dentystycznej rozsądne wydaje się stwierdzenie warunkowej niezależności zmiennych Toothache i Catch , biorąc pod uwagę Cavity :

Zauważ, że to twierdzenie jest nieco silniejsze niż Equation (12.17) , które zapewnia niezależność tylko dla określonych wartości Toothache i Catch . Podobnie jak w przypadku absolutnej niezależności w Równaniu, równoważne formy

można również użyć. Sekcja wykazała, że twierdzenia o absolutnej niezależności pozwalają na rozkład pełnego wspólnego podziału na znacznie mniejsze części. Okazuje się, że to samo dotyczy warunkowych twierdzeń o niezależności. Na przykład, biorąc pod uwagę twierdzenie w Równaniu , możemy wyprowadzić dekompozycję w następujący sposób:

Z pozoru reguła Bayesa nie wydaje się zbyt użyteczna. Pozwala nam obliczyć pojedynczy wyraz P(b|a) w postaci trzech wyrazów: P(a| b) ,P(b) i P(a) . Wydaje się, że to dwa kroki w tył; ale reguła Bayesa jest przydatna w praktyce, ponieważ w wielu przypadkach mamy dobre oszacowania prawdopodobieństwa dla tych trzech liczb i musimy obliczyć czwartą. Często postrzegamy jako dowód skutek jakiejś nieznanej przyczyny i chcielibyśmy tę przyczynę ustalić. W takim przypadku reguła Bayesa staje się

Prawdopodobieństwo warunkowe P(skutek | przyczyna) określa ilościowo zależność w kierunku przyczynowym, natomiast P(przyczyna | skutek) opisuje kierunek diagnostyczny. W zadaniu takim jak diagnoza medyczna często mamy warunkowe prawdopodobieństwa dotyczące związków przyczynowych. Lekarz zna P(objawy | choroba) i chce postawić diagnozę, P(choroba | objawy).

. Na przykład lekarz wie, że zapalenie opon mózgowych powoduje, że pacjent ma sztywność karku, powiedzmy, w 70% przypadków. Lekarz zna również pewne bezwarunkowe fakty: wcześniejsze prawdopodobieństwo, że którykolwiek pacjent ma zapalenie opon mózgowych wynosi 1/50 000, a wcześniejsze prawdopodobieństwo, że pacjent ma sztywność karku, wynosi 1%. Przyjmując propozycję, że pacjent ma sztywność karku, im propozycję, że pacjent ma zapalenie opon mózgowo-rdzeniowych, mamy

Oznacza to, że spodziewamy się, że tylko 0,14% pacjentów ze sztywnością karku będzie miało zapalenie opon mózgowych. Zauważ, że chociaż sztywność karku jest dość silnie wskazana przez zapalenie opon mózgowo-rdzeniowych (z prawdopodobieństwem 0,7), prawdopodobieństwo zapalenia opon mózgowych u pacjentów ze sztywnością karku pozostaje niewielkie. Dzieje się tak, ponieważ wcześniejsze prawdopodobieństwo sztywności karku (z jakiejkolwiek przyczyny) jest znacznie wyższe niż wcześniejsze w przypadku zapalenia opon mózgowych. Sekcja 12.3 zilustrowała proces, dzięki któremu można uniknąć oceny wcześniejszego prawdopodobieństwa, dowód (tutaj, P(s) ) poprzez obliczenie prawdopodobieństwa a posteriori dla każdej wartości zmiennej zapytania (tutaj, m i ¬m), a następnie znormalizowanie wyników. Ten sam proces można zastosować podczas korzystania z reguły Bayesa. Mamy

Tak więc, aby użyć tego podejścia, musimy oszacować P(s |¬m) zamiast P(s). Nie ma darmowego obiadu – czasem jest to łatwiejsze, czasem trudniejsze. Ogólna postać reguły Bayesa z normalizacją to

gdzie α jest stałą normalizacyjną potrzebną do zsumowania wpisów w P(Y|X) do 1. Jednym z oczywistych pytań, jakie należy zadać w związku z regułą Bayesa, jest to, dlaczego można mieć dostępne prawdopodobieństwo warunkowe w jednym kierunku, ale nie w drugim. Jeśli chodzi o zapalenie opon mózgowych, być może lekarz wie, że sztywność karku oznacza zapalenie opon mózgowych w 1 na 5000 przypadków; oznacza to, że lekarz ma informacje ilościowe w kierunku diagnostycznym od objawów do przyczyn. Taki lekarz nie musi stosować reguły Bayesa.

Niestety wiedza diagnostyczna jest często bardziej krucha niż wiedza przyczynowa. W przypadku nagłej epidemii zapalenia opon mózgowych bezwarunkowe prawdopodobieństwo wystąpienia zapalenia opon mózgowo-rdzeniowych, P(m), wzrośnie. Lekarz, który wyprowadził prawdopodobieństwo diagnostyczne P(m|s) bezpośrednio z obserwacji statystycznych pacjentów przed epidemią, nie będzie miał pojęcia, jak zaktualizować tę wartość, ale lekarz, który obliczy P(m|s) z pozostałych trzech wartości, zobaczy że P(m|s) powinno wzrosnąć proporcjonalnie do P(m) . Co najważniejsze, epidemia nie ma wpływu na informację o przyczynie P(s|m), ponieważ odzwierciedla ona po prostu sposób działania zapalenia opon mózgowych. Wykorzystanie tego rodzaju bezpośredniej wiedzy o przyczynach lub wiedzy opartej na modelach zapewnia kluczową odporność niezbędną, aby systemy probabilistyczne były wykonalne w świecie rzeczywistym.

Zdefiniowaliśmy regułę iloczynu. Można ją zapisać w dwóch formach:

Porównując dwie prawe strony i dzieląc przez P(a) otrzymujemy

To równanie jest znane jako reguła Bayesa (również prawo Bayesa lub twierdzenie Bayesa). To proste równanie leży u podstaw większości nowoczesnych systemów sztucznej inteligencji do wnioskowania probabilistycznego. Bardziej ogólny przypadek reguły Bayesa dla zmiennych wielowartościowych można zapisać w P w następujący sposób:

Tak jak poprzednio, należy to traktować jako reprezentację zestawu równań, z których każde dotyczy określonych wartości zmiennych. Będziemy mieli również okazję skorzystać z bardziej ogólnej wersji, uzależnionej od pewnych podstawowych dowodów e:

Rozszerzmy pełny rozkład łączny na rysunku, dodając czwartą zmienną, Weather.

Pełny rozkład stawu staje się wtedy  P(Toothache, Catch, Cavity, Weather), który ma 2x2x2x4=32 wpisy. Zawiera cztery „edycje” tabeli pokazanej na powyższym rysunku, po jednej dla każdego rodzaju pogody. Jaki związek mają te wydania ze sobą i z oryginalną tabelą trzech zmiennych? Jak ma się wartość P(toothache, catch, cavity, cloud) do wartości P(toothache, catch, cavity)? Możemy zastosować regułę produktu :

O ile nie zajmujemy się bóstwami, nie powinniśmy wyobrażać sobie, że problemy z zębami wpływają na pogodę. A przynajmniej w przypadku stomatologii w pomieszczeniach można bezpiecznie powiedzieć, że pogoda nie wpływa na zmienne uzębienia. Dlatego uzasadnione wydaje się następujące stwierdzenie:

Z tego możemy wywnioskować

Podobne równanie istnieje dla każdego wpisu w P(Ból zęba, Złap, Jamy, Pogoda) . W rzeczywistości możemy napisać ogólne równanie

Tak więc tablicę 32-elementową dla czterech zmiennych można zbudować z jednej tabeli 8-elementowej i jednej tabeli 4-elementowej. Rozkład ten przedstawiono schematycznie na rysunku (a).

Własność, której użyliśmy w równaniu to niezależność (również niezależność marginalna i niezależność absolutna). W szczególności pogoda jest niezależna od Twojego problemu z zębami. Niezależność między zdaniami a i b można zapisać jako

Wszystkie te formy są równoważne. Niezależność między zmiennymi X i Y można zapisać w następujący sposób (ponownie wszystkie są równoważne):

Twierdzenia o niezależności są zwykle oparte na znajomości dziedziny. Jak pokazuje przykład bólu zęba – pogoda, mogą one radykalnie zmniejszyć ilość informacji niezbędnych do określenia pełnego rozmieszczenia stawów. Jeżeli cały zbiór zmiennych można podzielić na niezależne podzbiory, wówczas pełny łączny rozkład można rozłożyć na oddzielne łączne rozkłady na tych podzbiorach. Na przykład, pełny łączny rozkład wyniku n niezależnych rzutów monetą P(C₁,…,C_n) ma 2ⁿ wpisów, ale można go przedstawić jako iloczyn n rozkładów pojedynczej zmiennej P(Ci). Mówiąc bardziej praktycznie, niezależność stomatologii i meteorologii jest dobrą rzeczą, ponieważ w przeciwnym razie praktyka dentystyczna może wymagać gruntownej znajomości meteorologii i na odwrót. Gdy są one dostępne, wówczas twierdzenia o niezależności mogą pomóc w zmniejszeniu rozmiaru reprezentacji domeny i złożoności problemu wnioskowania. Niestety, czyste oddzielenie całych zbiorów zmiennych przez niezależność jest dość rzadkie. Za każdym razem, gdy istnieje związek, jakkolwiek pośredni, między dwiema zmiennymi, niezależność nie zostanie utrzymana. Co więcej, nawet niezależne podzbiory mogą być dość duże – na przykład stomatologia może obejmować dziesiątki chorób i setki objawów, z których wszystkie są ze sobą powiązane. Aby poradzić sobie z takimi problemami, potrzebujemy bardziej subtelnych metod niż prosta koncepcja niezależności.

W tej sekcji opisujemy prostą metodę wnioskowania probabilistycznego – to jest obliczanie prawdopodobieństw a posteriori dla propozycji zapytań na podstawie zaobserwowanych dowodów. Pełną dystrybucję łączną wykorzystujemy jako „bazę wiedzy”, z której można uzyskać odpowiedzi na wszystkie pytania. Po drodze wprowadzamy również kilka przydatnych technik manipulowania równaniami obejmującymi prawdopodobieństwa. Zaczynamy od prostego przykładu: domeny składającej się tylko z trzech zmiennych logicznych Toothache, Cavity i Catch (paskudna stalowa sonda dentysty zaczepia się o mój ząb). Pełny rozkład połączeń wynosi 2 x 2 x 2 w tabeli, jak pokazano na rysunku

Zauważ, że prawdopodobieństwa w łącznym rozkładzie sumują się do 1, jak wymagają tego aksjomaty prawdopodobieństwa. Zauważ również, że Równanie daje nam bezpośredni sposób obliczania prawdopodobieństwa dowolnego zdania, prostego lub złożonego: po prostu zidentyfikuj te możliwe światy, w których zdanie jest prawdziwe i dodaj ich prawdopodobieństwa. Na przykład istnieje sześć możliwych światów, w których cavity V toothache utrzymuje:

Jednym ze szczególnie powszechnych zadań jest wyodrębnienie rozkładu dla pewnego podzbioru zmiennych lub pojedynczej zmiennej. Na przykład dodanie wpisów w pierwszym wierszu daje bezwarunkowe lub marginalne prawdopodobieństwo wystąpienia wgłębienia:

Proces ten nazywa się marginalizacją lub sumowaniem — ponieważ sumujemy prawdopodobieństwa dla każdej możliwej wartości innych zmiennych, tym samym usuwając je z równania. Dla dowolnych zbiorów zmiennych Y i Z możemy napisać następującą ogólną regułę marginalizacji:

gdzie Σ_z sumuje wszystkie możliwe kombinacje wartości zbioru zmiennych Z. Jak zwykle możemy w tym równaniu skrócić P(Y,Z = z) przez P(Y,z). Dla przykładu Cavity, Equation odpowiada następującemu równaniu:

Korzystając z reguły iloczynu , możemy zastąpić P(Y,z) w równaniu przez P(Y|z)P(z) , otrzymując regułę zwaną warunkowaniem:

Marginalizacja i warunkowanie okazują się użytecznymi regułami dla wszelkiego rodzaju wyprowadzeń zawierających wyrażenia probabilistyczne. W większości przypadków interesuje nas obliczenie prawdopodobieństw warunkowych niektórych zmiennych, biorąc pod uwagę dowody dotyczące innych. Prawdopodobieństwa warunkowe można znaleźć, używając najpierw równania  w celu uzyskania wyrażenia w kategoriach prawdopodobieństw bezwarunkowych, a następnie oceniając wyrażenie z pełnego rozkładu łącznego. Na przykład, możemy obliczyć prawdopodobieństwo ubytku, biorąc pod uwagę oznaki bólu zęba, w następujący sposób:

Aby to sprawdzić, możemy również obliczyć prawdopodobieństwo, że nie ma ubytku, biorąc pod uwagę ból zęba:

Obie wartości sumują się do 1,0, tak jak powinny. Zauważ, że mianownikiem obu tych obliczeń jest termin P (ból zęba). Gdyby zmienna Cavity miała więcej niż dwie wartości, byłaby w mianowniku dla nich wszystkich. W rzeczywistości można ją postrzegać jako stałą normalizacyjną dla rozkładu P (jamka | ból zęba), zapewniając, że sumuje się ona do 1. W rozdziałach dotyczących prawdopodobieństwa używamy α do oznaczania takich stałych. Za pomocą tego zapisu możemy zapisać dwa poprzednie równania w jednym:

Innymi słowy, możemy obliczyć P(Jama | Ból zęba), nawet jeśli nie znamy wartości P(ból zęba)! Chwilowo zapominamy o współczynniku 1/P (ból zęba) i sumujemy wartości dla cavity i ¬cavity , otrzymując 0,12 i 0,08. To są prawidłowe proporcje względne, ale nie sumują się do 1, więc normalizujemy je dzieląc każdy przez 0,12 +0,08 , otrzymując prawdziwe prawdopodobieństwa 0,6 i 0,4. Normalizacja okazuje się przydatnym skrótem w wielu obliczeniach prawdopodobieństwa, zarówno w celu ułatwienia obliczeń, jak i umożliwienia nam kontynuacji, gdy niektóre oceny prawdopodobieństwa (takie jak P(ból zęba) ) nie są dostępne. Z przykładu możemy wyodrębnić ogólną procedurę wnioskowania. Zaczniemy od przypadku, w którym zapytanie obejmuje pojedynczą zmienną, X (w przykładzie Cavity). Niech E będzie listą zmiennych dowodowych (w przykładzie tylko Ból zęba), niech e będzie listą obserwowanych dla nich wartości, a Y będzie pozostałymi zmiennymi nieobserwowanymi (w przykładzie tylko Złap). Zapytanie to P(X|c) i może być ocenione jako

gdzie sumowanie obejmuje wszystkie możliwe y (tj. wszystkie możliwe kombinacje wartości nieobserwowanych zmiennych Y ). Zauważ, że razem zmienne X , E i Y tworzą kompletny zbiór zmiennych dla dziedziny, więc P(X,e,y) jest po prostu podzbiorem prawdopodobieństw z pełnego łącznego rozkładu. Biorąc pod uwagę pełny rozkład łączny do pracy, równanie (12.9) może odpowiadać na pytania probabilistyczne dla zmiennych dyskretnych. Nie skaluje się jednak dobrze: dla dziedziny opisanej przez n zmiennych logicznych, wymaga tabeli wejściowej o rozmiarze O(2ⁿ) i zajmuje czas O(2ⁿ) na przetworzenie tabeli. W realistycznym zadaniu moglibyśmy z łatwością mieć n = 100 , czyniąc O(2ⁿ) niepraktycznym – tabela z 2¹⁰⁰ ≈ 10³⁰ wpisami! Problemem nie jest tylko pamięć i obliczenia: prawdziwy problem polega na tym, że jeśli każde z 1030 prawdopodobieństw ma być oszacowane oddzielnie od przykładów, liczba wymaganych przykładów będzie astronomiczna. Z tych powodów pełny podział łączny w formie tabelarycznej rzadko jest praktycznym narzędziem do budowania systemów rozumowania. Zamiast tego należy ją postrzegać jako teoretyczną podstawę, na której można budować bardziej efektywne podejścia, podobnie jak tabele prawdy stanowiły teoretyczną podstawę dla bardziej praktycznych algorytmów, takich jak DPLL

Równania implikują pewne relacje między stopniami przekonań, które można przypisać logicznie powiązanym zdaniom. Na przykład możemy wyprowadzić znajomy związek między prawdopodobieństwem zdania a prawdopodobieństwem jego negacji:

Możemy również wyprowadzić dobrze znany wzór na prawdopodobieństwo alternatywy, zwany czasem zasadą włączenia – wykluczenia:

Zasadę tę łatwo zapamiętać, zauważając, że przypadki, w których zachodzi, wraz z przypadkami, w których zachodzi, z pewnością obejmują wszystkie przypadki, w których zachodzi a V b; ale zsumowanie tych dwóch zbiorów przypadków liczy ich przecięcie dwukrotnie, więc musimy odjąć P (a Λ b).

Tego rodzaju pytanie było przedmiotem dziesięcioleci intensywnej debaty między zwolennikami wykorzystywania prawdopodobieństw jako jedynej uzasadnionej formy stopni wiary, a zwolennikami alternatywnych podejść. Jeden z argumentów przemawiających za aksjomatami prawdopodobieństwa, po raz pierwszy przedstawiony przez Bruno de Finetti w 1931 r., jest następujący: jeśli agent ma pewien stopień wiary w twierdzenie a , to agent powinien być w stanie określić szanse, przy których jest obojętny na postawić za lub przeciwko . Pomyśl o tym jako o grze między dwoma agentami: Agent 1 stwierdza: „moja wiara w zdarzenie a wynosi 0,4”. Agent 2 ma wtedy swobodę wyboru, czy postawić za, czy przeciwko stawkom, które są zgodne z określonym stopniem wiary. Oznacza to, że Agent 2 może zaakceptować zakład Agenta 1, że nastąpi awaria, oferując 6 USD przeciwko 4 USD Agenta 1. Lub Agent 2 może zaakceptować zakład Agenta 1, że wystąpi ¬a, oferując 4 USD przeciwko 6 USD Agenta 1. Następnie obserwujemy wynik , a kto ma rację, zbiera pieniądze. Jeśli czyjeś stopnie wiary nie odzwierciedlają dokładnie świata, można oczekiwać, że w dłuższej perspektywie straci pieniądze na rzecz przeciwnika, którego przekonania dokładniej odzwierciedlają stan świata. Twierdzenie De Finettiego nie dotyczy wyboru właściwych wartości dla poszczególnych prawdopodobieństw, ale wyboru wartości dla prawdopodobieństw logicznie powiązanych zdań: Jeśli Agent 1 wyraża zestaw stopni przekonań, które naruszają aksjomaty teorii prawdopodobieństwa, wówczas istnieje kombinacja zakłady Agenta 2, które gwarantują, że Agent 1 za każdym razem straci pieniądze. Załóżmy na przykład, że Agent 1 ma zestaw stopni wiary z równania . Rysunek pokazuje, że jeśli Agent 2 zdecyduje się postawić 4 USD na a , 3 USD na b i 2 USD na ¬(aVb) , to Agent 1 zawsze traci pieniądze, niezależnie od wyników a i b . Twierdzenie De Finettiego implikuje, że żaden racjonalny podmiot nie może mieć przekonań, które naruszają aksjomaty prawdopodobieństwa.

Jednym z powszechnych zarzutów wobec twierdzenia de Finettiego jest to, że ta gra w zakłady jest dość wymyślna. Na przykład, co się stanie, jeśli ktoś odmówi postawienia? Czy to kończy kłótnię? Odpowiedź brzmi: gra w zakłady jest abstrakcyjnym modelem sytuacji decyzyjnej, w której każdy agent jest nieuchronnie zaangażowany w każdym momencie. Każde działanie (w tym bezczynność) jest rodzajem zakładu, a każdy wynik może być postrzegany jako wypłata zakładu. Odmowa obstawiania jest jak odmawianie upłynięcia czasu. Wysunięto inne silne argumenty filozoficzne przemawiające za wykorzystaniem prawdopodobieństw, w szczególności argumenty Coxa (1946), Carnapa (1950) i Jaynesa (2003). Każdy z nich konstruuje zbiór aksjomatów do rozumowania ze stopniami przekonań: brak sprzeczności, zgodność ze zwykłą logiką (na przykład, jeśli wiara w A rośnie, to wiara w -A musi spaść) i tak dalej. Jedynym kontrowersyjnym aksjomatem jest to, że stopnie wiary muszą być liczbami lub przynajmniej zachowywać się jak liczby, ponieważ muszą być przechodnie (jeśli wiara w A jest większa niż wiara w B, która jest większa niż wiara w C, to wiara w A musi być większe niż C) i porównywalne (przekonanie w A musi być równe, większe lub mniejsze niż przekonanie w B ). Można wtedy udowodnić, że prawdopodobieństwo jest jedynym podejściem, które spełnia te aksjomaty. Jednak świat jest taki, jaki jest, praktyczne demonstracje czasami przemawiają głośniej niż dowody. Sukces systemów rozumowania opartych na teorii prawdopodobieństwa był znacznie skuteczniejszy niż argumenty filozoficzne w nawracaniu. Przyjrzymy się teraz, w jaki sposób aksjomaty można zastosować do wnioskowania.

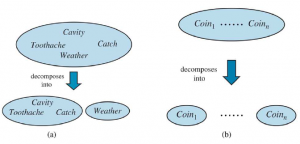
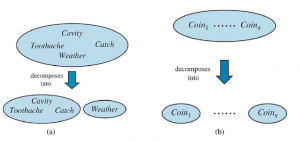
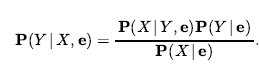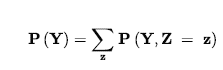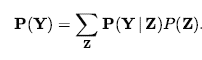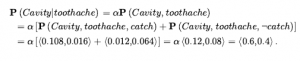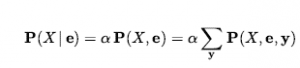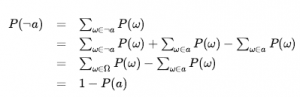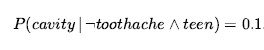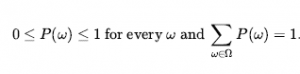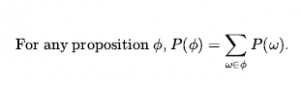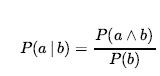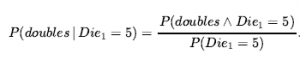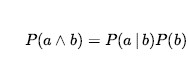Zdania opisujące zbiory możliwych światów są zwykle pisane w notacji, która łączy elementy logiki zdań i notacji spełniania ograniczeń. W terminologii sekcji 2.4.7 jest to reprezentacja podzielona na czynniki, w której możliwy świat jest reprezentowany przez zestaw par zmienna/wartość. Możliwa jest również bardziej ekspresyjna reprezentacja strukturalna, jak pokazano w rozdziale 15 . Zmienne w teorii prawdopodobieństwa nazywane są zmiennymi losowymi, a ich nazwy zaczynają się od dużej litery. Zatem w przykładzie z kostką Total i Die1 są zmiennymi losowymi. Każda zmienna losowa jest funkcją, która odwzorowuje z dziedziny możliwych światów OMEGA na pewien zakres – zbiór możliwych wartości, które może przyjąć. Zakres sumy dla dwóch kości to zestaw {2…12}, a zakres kości1 to {1…6} . Nazwy wartości są zawsze pisane małymi literami, więc możemy napisać SIGMA, aby sumować wartości X . Zmienna losowa typu Boolean ma zakres {true, false} . na przykład twierdzenie, że wyrzucono podwajania, można zapisać jako Double = true . (Alternatywnym zakresem dla zmiennych logicznych jest zbiór {0,1} , w którym to przypadku zmienna ma rozkład Bernoulliego.) Zgodnie z konwencją, zdania w postaci A = prawda są skracane po prostu jako a , podczas gdy A = fałsz jest skrócony jako ¬a. (Stosowanie dubletów, ubytku i bólu zęba w poprzedniej sekcji to skróty tego rodzaju.)

Zakresy mogą być zestawami dowolnych tokenów. Możemy wybrać przedział wiekowy jako zestaw {młodzież, nastolatek, dorosły}, a przedział Pogody może być {słońce, deszcz, chmura, śnieg}. Gdy żadna dwuznaczność nie jest możliwa, często używa się samej wartości jako zdania, że dana zmienna ma tę wartość; tak więc słońce może oznaczać Pogoda = słońce. Wszystkie powyższe przykłady mają skończone zakresy. Zmienne mogą mieć również nieskończone zakresy — albo dyskretne (jak liczby całkowite) albo ciągłe (jak liczby rzeczywiste). W przypadku dowolnej zmiennej o uporządkowanym zakresie dozwolone są również nierówności, takie jak

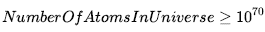
Wreszcie możemy łączyć tego rodzaju zdania elementarne (w tym skrócone formy zmiennych boolowskich) za pomocą spójników logiki zdań. Na przykład możemy wyrazić „Prawdopodobieństwo, że pacjentka ma ubytek, biorąc pod uwagę, że jest nastolatką bez bólu zęba, wynosi 0,1” w następujący sposób:

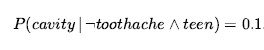
W notacji prawdopodobieństwa często używa się przecinka dla koniunkcji, więc możemy napisać

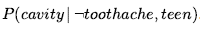
Czasami będziemy chcieli porozmawiać o prawdopodobieństwach wszystkich możliwych wartości zmiennej losowej. Moglibyśmy napisać:

ale jako skrót pozwolimy

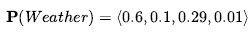
gdzie P wskazuje, że wynik jest wektorem liczb, a gdzie zakładamy predefiniowane uporządkowanie <słońce, deszcz, chmura, śnieg> na zakresie Pogoda . Mówimy, że zdanie P definiuje rozkład prawdopodobieństwa dla zmiennej losowej Wheater – czyli przypisanie prawdopodobieństwa dla każdej możliwej wartości zmiennej losowej. (W tym przypadku, przy skończonym, dyskretnym zakresie, rozkład nazywamy rozkładem kategorycznym). Notacja P jest również używana dla rozkładów warunkowych: P(X|Y) daje wartości P(X = xi | Y = yj) dla każdej możliwej pary i , j.

Dla zmiennych ciągłych nie jest możliwe wypisanie całego rozkładu jako wektora, ponieważ wartości jest nieskończenie wiele. Zamiast tego możemy zdefiniować prawdopodobieństwo, że zmienna losowa przyjmie pewną wartość jako sparametryzowaną funkcję , zwykle nazywaną funkcją gęstości prawdopodobieństwa. Na przykład zdanie

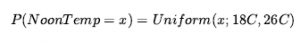
wyraża przekonanie, że temperatura w południe rozkłada się równomiernie między 18 a 26 stopni Celsjusza. Funkcje gęstości prawdopodobieństwa (czasami nazywane plikami pdf) różnią się znaczeniem od rozkładów dyskretnych. Powiedzenie, że gęstość prawdopodobieństwa jest jednolita w zakresie od 18°C do 26°C oznacza, że istnieje 100% szansa, że temperatura spadnie gdzieś w regionie o szerokości 18°C i 50% szansa, że spadnie ona w dowolnym podregionie o szerokości 4°C, oraz wkrótce. Piszemy gęstość prawdopodobieństwa dla ciągłej zmiennej losowej X o wartości x jako P(X = x) lub po prostu P(x) ; intuicyjna definicja P(x) to prawdopodobieństwo, że X mieści się w dowolnie małym obszarze zaczynającym się od x , podzielone przez szerokość obszaru:

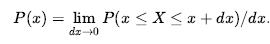
Dla NoonTemp mamy

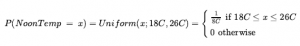
gdzie C oznacza stopnie Celsjusza (nie stałą). W P(NoonTemp = 20,18C) = 1/8C zauważ, że 1/8C nie jest prawdopodobieństwem, jest gęstością prawdopodobieństwa. Prawdopodobieństwo, że NoonTemp wynosi dokładnie 20.18C wynosi zero, ponieważ 20.18C jest regionem o szerokości 0. Niektórzy autorzy używają różnych symboli dla dyskretnych prawdopodobieństw i gęstości prawdopodobieństw; używamy P dla określonych wartości prawdopodobieństwa i P dla wektorów wartości w obu przypadkach, ponieważ zamieszanie rzadko się pojawia, a równania są zwykle identyczne. Zauważ, że prawdopodobieństwa są liczbami niemianowanymi, podczas gdy funkcje gęstości są mierzone jednostką, w tym przypadku odwrotnością stopni Celsjusza. Jeśli ten sam przedział temperatury miałby być wyrażony w stopniach Fahrenheita, miałby szerokość 14,4 stopnia, a gęstość wynosiłaby 1/14,4 F . Oprócz rozkładów na pojedynczych zmiennych potrzebujemy notacji dla rozkładów na wielu zmiennych. Używa się do tego przecinków. Na przykład P(Weather,Cavity) oznacza prawdopodobieństwa wszystkich kombinacji wartości Weather i Cavity . Jest to tabela prawdopodobieństw 4 x 2 zwana łącznym rozkładem prawdopodobieństwa pogody i jamy. Możemy również mieszać zmienne i określone wartości; P(sun,Cavity) byłby dwuelementowym wektorem podającym prawdopodobieństwa wnęki w słoneczny dzień i braku wnęki w słoneczny dzień.

Notacja P sprawia, że niektóre wyrażenia są znacznie bardziej zwięzłe, niż mogłyby być w innym przypadku. Na przykład reguły iloczynów dla wszystkich możliwych wartości pogody i wnęki można zapisać jako pojedyncze równanie:

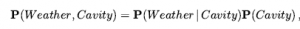
Jako przypadek zdegenerowany, P(słońce, wnęka) nie ma zmiennych, a zatem jest wektorem zerowym, który możemy traktować jako wartość skalarną. Teraz zdefiniowaliśmy składnię zdań i twierdzeń prawdopodobieństwa i podaliśmy część semantyki: Równanie definiuje prawdopodobieństwo zdania jako sumy prawdopodobieństw światów, w których ono zachodzi. Aby uzupełnić semantykę, musimy powiedzieć, czym są światy i jak określić, czy zdanie ma zastosowanie w świecie. Zapożyczamy tę część bezpośrednio z semantyki logiki zdań w następujący sposób. Świat możliwy jest definiowany jako przypisanie wartości do wszystkich rozważanych zmiennych losowych. Łatwo zauważyć, że ta definicja spełnia podstawowy wymóg, aby możliwe światy wzajemnie się wykluczały i były wyczerpujące (Ćwiczenie 12.EXEX). Na przykład, jeśli zmienne losowe są Cavity, Tothache i Weather , to jest 2 x 2 x 4 = 16 możliwych światów. Co więcej, prawdziwość dowolnego zdania można łatwo określić w takich światach za pomocą tego samego rekurencyjnego obliczania prawdziwości, którego używaliśmy do logiki zdań. Należy zauważyć, że niektóre zmienne losowe mogą być zbędne, ponieważ ich wartości można uzyskać we wszystkich przypadkach z wartości innych zmiennych. Na przykład zmienna Doubles w świecie dwóch kości jest prawdziwa dokładnie wtedy, gdy Die1 – Die2 . Włączenie Doubles jako jednej ze zmiennych losowych, oprócz Die1 i Die2, wydaje się zwiększać liczbę możliwych światów od 36 do 72, ale oczywiście dokładnie połowa z 72 będzie logicznie niemożliwa i będzie miała prawdopodobieństwo 0. Z powyższej definicji światów możliwych wynika, że ​​model prawdopodobieństwa jest całkowicie określony przez łączny rozkład dla wszystkich zmiennych losowych – tzw. pełny wspólny rozkład prawdopodobieństwa. Na przykład, biorąc pod uwagę Cavity , Toothache i Weather , pełny rozkład stawów to P (Cavity , Toothache , Weather) . Ten wspólny rozkład można przedstawić jako tabelę 2 x 2 x 4 z 16 wpisami. Ponieważ prawdopodobieństwo każdego zdania jest sumą światów możliwych, pełny łączny rozkład w zasadzie wystarcza do obliczenia prawdopodobieństwa dowolnego zdania.

Podobnie jak twierdzenia logiczne, twierdzenia probabilistyczne dotyczą światów możliwych. Podczas gdy twierdzenia logiczne mówią, które światy możliwe są ściśle wykluczone (wszystkie te, w których twierdzenie jest fałszywe), twierdzenia probabilistyczne mówią o prawdopodobieństwie różnych światów. W teorii prawdopodobieństwa zbiór wszystkich możliwych światów nazywamy przestrzenią prób. Światy możliwe wzajemnie się wykluczają i wyczerpują — dwa światy możliwe nie mogą mieć miejsca i jeden świat możliwy musi mieć miejsce. Na przykład, jeśli mamy rzucić dwiema (rozróżnialnymi) kośćmi, do rozważenia jest 36 możliwych światów: (1,1), (1,2), …, (6,6). Grecka litera Ω (wielka litera omega) odnosi się do przestrzeni próbki, a ω (mała litera omega) do elementów przestrzeni, czyli poszczególnych światów możliwych. W pełni określony model prawdopodobieństwa wiąże prawdopodobieństwo liczbowe P(ω) z każdym możliwym światem. Podstawowe aksjomaty teorii prawdopodobieństwa mówią, że każdy możliwy świat ma prawdopodobieństwo od 0 do 1, a całkowite prawdopodobieństwo zbioru możliwych światów wynosi 1:

Na przykład, jeśli założymy, że każda kostka jest sprawiedliwa, a rzuty nie kolidują ze sobą, to każdy z możliwych światów (1,1), (1,2), …, (6,6) ma prawdopodobieństwo 1 /36 . Jeśli kostki zostaną załadowane, niektóre światy będą miały wyższe prawdopodobieństwa, a inne niższe, ale wszystkie nadal będą sumować się do 1. Probabilistyczne twierdzenia i zapytania zwykle nie dotyczą konkretnych światów możliwych, ale ich zbiorów. Na przykład możemy zapytać o prawdopodobieństwo, że obie kostki sumują się do 11, prawdopodobieństwo wyrzucenia podwojeń i tak dalej. W teorii prawdopodobieństwa zbiory te nazywa się zdarzeniami – termin ten był już szeroko stosowany w rozdziale 10 dla innego pojęcia. W logice zbiór światów odpowiada zdaniu w języku formalnym; konkretnie, dla każdego zdania, odpowiadający mu zbiór zawiera tylko te możliwe światy, w których to zdanie się zgadza. (Dlatego „zdarzenie” i „zdanie” oznaczają w tym kontekście mniej więcej to samo, z wyjątkiem tego, że zdanie jest wyrażone w języku formalnym.) Prawdopodobieństwo związane ze zdaniem definiuje się jako sumę prawdopodobieństw światów w które posiada:

Na przykład, rzucając uczciwymi kośćmi, mamy P(TOTAL =11) = P((5,6))+ P((6,5)) = 1/36 + 1/36 =1/18 . Zauważ, że teoria prawdopodobieństwa nie wymaga pełnej wiedzy o prawdopodobieństwach każdego możliwego świata. Na przykład, jeśli wierzymy, że kostki spiskują w celu uzyskania tej samej liczby, możemy stwierdzić, że P(podwaja się) = 1/4, nie wiedząc, czy kostki wolą podwójne 6 od podwojenia 2. Podobnie jak w przypadku twierdzeń logicznych, to twierdzenie ogranicza podstawowe model prawdopodobieństwa bez pełnego jego określenia. Prawdopodobieństwa takie jak P(TOTAL = 11) i P(doubles) są nazywane bezwarunkowymi lub uprzednimi prawdopodobieństwami (a czasami po prostu „priory” w skrócie); odnoszą się do stopni wiary w twierdzenia przy braku innych informacji. Jednak przez większość czasu mamy pewne informacje, zwykle nazywane dowodami, które zostały już ujawnione. Na przykład pierwsza kostka może już wskazywać 5 i czekamy z zapartym tchem, aż druga przestanie się obracać. W takim przypadku nie interesuje nas bezwarunkowe prawdopodobieństwo wyrzucenia dubletu, ale prawdopodobieństwo warunkowe lub a posteriori (lub po prostu „a posteriori” w skrócie) wyrzucenia dubletu, biorąc pod uwagę, że pierwsza kostka to 5. To prawdopodobieństwo jest zapisane jako P(podwaja | Kość1 = 5), gdzie „|” jest wymawiane jako „dane”.

Podobnie, jeśli idę do dentysty na regularnie zaplanowaną kontrolę, wówczas interesujące może być prawdopodobieństwo a priori P(jamka) = 0,2; ale jeśli pójdę do dentysty, bo boli mnie ząb, liczy się prawdopodobieństwo warunkowe P(próchnica|ból zęba) = 0,6. Ważne jest, aby zrozumieć, że P (jamka) = 0,2 jest nadal ważne po zaobserwowaniu bólu zęba; to po prostu nie jest szczególnie przydatne. Przy podejmowaniu decyzji agent musi opierać się na wszystkich zaobserwowanych dowodach. Ważne jest również zrozumienie różnicy między warunkowaniem a implikacją logiczną. Twierdzenie, że P(próchnica|ból zęba) = 0,6 nie oznacza „Kiedy ból zęba jest prawdziwy, wywnioskuj, że ubytek jest prawdziwy z prawdopodobieństwem 0,6”, a raczej „Gdy ból zęba jest prawdziwy i nie mamy dalszych informacji, wywnioskuj, że ubytek jest prawdziwy z prawdopodobieństwo 0,6.” Dodatkowy warunek jest ważny; na przykład, gdybyśmy mieli dalsze informacje, że dentysta nie znalazł ubytków, zdecydowanie nie chcielibyśmy wnioskować, że ubytek jest prawdziwy z prawdopodobieństwem 0,6; zamiast tego musimy użyć

Mówiąc matematycznie, prawdopodobieństwa warunkowe definiuje się w kategoriach prawdopodobieństw bezwarunkowych w następujący sposób: dla dowolnych zdań a i b mamy

który posiada zawsze P(b) > 0  . Na przykład

 

Definicja ma sens, jeśli pamiętasz, że obserwowanie b wyklucza wszystkie możliwe światy, w których b jest fałszywe, pozostawiając zbiór, którego całkowite prawdopodobieństwo wynosi tylko P(b) . W ramach tego zbioru światy, w których a jest prawdziwe, muszą spełniać a Λ b i stanowić ułamek P( aΛb) / P(b). Definicję prawdopodobieństwa warunkowego, można zapisać w innej postaci zwanej regułą iloczynu:

Aby nasz agent mógł reprezentować i wykorzystywać informacje probabilistyczne, potrzebujemy języka formalnego. Język teorii prawdopodobieństwa był tradycyjnie nieformalny, pisany przez ludzkich matematyków dla innych ludzkich matematyków. Przyjmujemy podejście bardziej dopasowane do potrzeb AI i łączymy je z koncepcjami logiki formalnej.

Zastanów się ponownie nad planem dojazdu na lotnisko A90. Załóżmy, że daje nam to 97% szans na złapanie naszego lotu. Czy to oznacza, że ​​jest to racjonalny wybór? Niekoniecznie: mogą istnieć inne plany, takie jak A180, z wyższym prawdopodobieństwem. Jeśli ważne jest, aby nie spóźnić się na lot, warto zaryzykować dłuższe oczekiwanie na lotnisku. A co z A1440, planem, który zakłada opuszczenie domu z 24-godzinnym wyprzedzeniem? W większości przypadków nie jest to dobry wybór, bo choć niemal gwarantuje dotarcie na czas, wiąże się z niemożliwym do zniesienia oczekiwaniem – nie mówiąc już o prawdopodobnie nieprzyjemnej diecie w postaci jedzenia na lotnisku. Aby dokonać takich wyborów, agent musi najpierw mieć preferencje wśród różnych możliwych wyników różnych planów. Efektem jest całkowicie określony stan, uwzględniający takie czynniki jak przybycie agenta na czas oraz długość oczekiwania na lotnisku. Używamy teorii użyteczności do reprezentowania preferencji i rozumowania za ich pomocą ilościowo. (Termin użyteczność jest tutaj używany w znaczeniu „jakość bycia użytecznym”, a nie w znaczeniu przedsiębiorstwa elektrycznego lub wodociągowego). Teoria użyteczności mówi, że każdy stan (lub sekwencja stanów) ma pewien stopień użyteczności lub użyteczności dla agenta i że agent będzie preferował stany o wyższej użyteczności. Użyteczność państwa zależy od agenta. Na przykład użyteczność stanu, w którym biały zamatował czarnego w grze w szachy, jest oczywiście wysoka dla agenta grającego białymi, ale niska dla agenta grającego czarnymi. Ale nie możemy kierować się wyłącznie wynikami 1, 1/2 i 0, które są podyktowane zasadami turniejowych szachów – niektórzy gracze (w tym autorzy) mogą być zachwyceni remisem z mistrzem świata, podczas gdy inni ( w tym byłego mistrza świata) może nie. Nie bierze się pod uwagę gustu ani preferencji: można by pomyśleć, że agent, który woli lody z gumą do żucia jalapeño od kawałka czekolady, jest dziwny, ale nie można powiedzieć, że agent jest irracjonalny. Funkcja użyteczności może odpowiadać za dowolny zestaw preferencji — dziwacznych lub typowych, szlachetnych lub perwersyjnych. Zwróć uwagę, że przedsiębiorstwa użyteczności publicznej mogą wyjaśniać altruizm, po prostu włączając dobro innych jako jeden z czynników. Preferencje, wyrażone przez użyteczności, są połączone z prawdopodobieństwami w ogólnej teorii racjonalnych decyzji zwanej teorią decyzji:

Fundamentalną ideą teorii decyzji jest to, że podmiot jest racjonalny wtedy i tylko wtedy, gdy wybiera działanie, które daje najwyższą oczekiwaną użyteczność, uśrednioną względem wszystkich możliwych skutków działania. Nazywa się to zasadą maksymalnej oczekiwanej użyteczności (MEU). W tym przypadku „oczekiwany” oznacza „średnią” lub „średnią statystyczną” użyteczności wyniku, ważoną prawdopodobieństwem wyniku. Widzieliśmy tę zasadę w działaniu, kiedy pokrótce poruszyliśmy temat optymalnych decyzji w tryktraku; jest to w rzeczywistości całkowicie ogólna zasada podejmowania decyzji przez jednego agenta. Rysunek przedstawia strukturę agenta, który wykorzystuje teorię decyzji do wybierania działań.

Agent jest identyczny, na abstrakcyjnym poziomie, z agetami które utrzymują stan przekonań odzwierciedlający dotychczasową historię percepcji. Podstawowa różnica polega na tym, że stan przekonań podmiotu podejmującego teorię decyzji reprezentuje nie tylko możliwości stanów świata, ale także ich prawdopodobieństwa. Biorąc pod uwagę stan przekonania i pewną wiedzę o skutkach działań, agent może dokonać probabilistycznych przewidywań wyników działania, a tym samym wybrać działanie o najwyższej oczekiwanej użyteczności.

Skoncentrujemy się na ogólnym zadaniu przedstawiania i obliczania z wykorzystaniem informacji probabilistycznych. Zajmiemy się metodami wykonywania konkretnych zadań przedstawiania i aktualizowania stanu przekonań w czasie oraz przewidywania wyników. Przyjrzymy się sposobom łączenia teorii prawdopodobieństwa z ekspresyjnymi językami formalnymi, takimi jak logika pierwszego rzędu i języki programowania ogólnego przeznaczenia. Bardziej szczegółowo omówmiy teorię użyteczności, i rozwiiemy algorytmy planowania sekwencji działań w środowiskach stochastycznych. Obejmiemy rozszerzenie tych pomysłów na środowiska wieloagentowe.