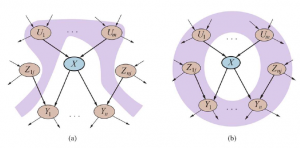
Z semantyki sieci Bayesa zdefiniowanej w równaniu (13.2) możemy wyprowadzić szereg warunkowych własności niezależności. Widzieliśmy już właściwość, że zmienna jest warunkowo niezależna od swoich innych poprzedników, biorąc pod uwagę jej rodziców. Możliwe jest również udowodnienie bardziej ogólnej właściwości „niepotomnych”, że: Każda zmienna jest warunkowo niezależna od swoich niepotomków, biorąc pod uwagę jej rodziców. Na przykład na rysunku zmienna JohnCalls jest niezależna od włamań, trzęsień ziemi i MarrryCalls, biorąc pod uwagę wartość Alarm. Definicja jest zilustrowana na rysunku (a)
Okazuje się, że własność niepotomków w połączeniu z interpretacją parametrów sieci θ (Xi|Parents(Xi)) jako prawdopodobieństw warunkowych P(Xi|Parents(Xi)) wystarcza do odtworzenia pełnego wspólnego rozkładu podanego w równaniu (13.2) . Innymi słowy, można inaczej spojrzeć na semantykę sieci Bayesa: zamiast definiować pełny łączny rozkład jako iloczyn rozkładów warunkowych, sieć definiuje zbiór warunkowych własności niezależności. Na podstawie tych właściwości można wyprowadzić pełny rozkład połączeń. Inna ważna własność niezależności wynika z własności nie-potomków: zmienna jest warunkowo niezależna od wszystkich innych węzłów w sieci, biorąc pod uwagę jej rodziców, dzieci i rodziców dzieci – czyli biorąc pod uwagę jej koc Markowa.
Na przykład zmienna Burglary jest niezależna od JohnCalls i MaryCalls , biorąc pod uwagę Alarm i Earthquake. Ta właściwość jest zilustrowana na rysunku (b). Właściwość koca Markowa umożliwia algorytmy wnioskowania, które wykorzystują całkowicie lokalne i rozproszone procesy próbkowania stochastycznego.
Najbardziej ogólnym pytaniem o warunkową niezależność, jakie można zadać w sieci Bayesa, jest to, czy zbiór węzłów X jest warunkowo niezależny od innego zbioru Y, biorąc pod uwagę trzeci zbiór Z. Można to skutecznie określić, badając sieć Bayesa, aby zobaczyć, czy Z d-oddziela X i Y. Proces przebiega w następujący sposób:
- Rozważmy tylko podwykres przodków składający się z X , Y , Z , i ich przodków.
- Dodaj linki między dowolną niepołączoną parą węzłów, które mają wspólne dziecko; teraz mamy tak zwany wykres moralny.
- Zastąp wszystkie linki skierowane linkami nieskierowanymi.
- Jeśli Z blokuje wszystkie ścieżki pomiędzy X i Y w wynikowym wykresie, wtedy Z d oddziela X i Y . W takim przypadku X jest warunkowo niezależne od Y, biorąc pod uwagę Z . W przeciwnym razie oryginalna sieć Bayesa nie wymaga warunkowej niezależności.
Krótko mówiąc, d-separacja oznacza separację w nieukierunkowanym, moralizowanym podgrafie przodków. Stosując definicję do sieci włamaniowej z rysunku 13.2 możemy wywnioskować, że włamanie i trzęsienie ziemi są niezależne, biorąc pod uwagę pusty zbiór (tj. są całkowicie niezależne); że nie muszą być warunkowo niezależne w przypadku alarmu; oraz że JohnCalls i MarryCalls są warunkowo niezależne od danego Alarmu. Zauważ również, że właściwość koc Markowa wynika bezpośrednio z własności d-separation, ponieważ koc Markowa zmiennej d-oddziela ją od wszystkich innych zmiennych.