Oprócz tego, że jest kompletną i nieredundantną reprezentacją domeny, sieć Bayesa może często być znacznie bardziej zwarta niż pełna wspólna dystrybucja. Ta właściwość umożliwia obsługę domen z wieloma zmiennymi. Zwartość sieci bayesowskich jest przykładem ogólnej właściwości systemów o strukturze lokalnej (zwanych również rzadkimi). W systemie o strukturze lokalnej każdy podkomponent oddziałuje bezpośrednio tylko z ograniczoną liczbą innych komponentów, niezależnie od całkowitej liczby komponentów. Struktura lokalna jest zwykle kojarzona z liniowym, a nie wykładniczym wzrostem złożoności. W przypadku sieci Bayesa uzasadnione jest przypuszczenie, że w większości domen każda z nich jest losowa na zmienną bezpośrednio wpływają co najwyżej inne, dla niektórych stała k . Jeśli dla uproszczenia przyjmiemy n zmiennych logicznych, to ilość informacji potrzebnych do określenia każdej tabeli prawdopodobieństwa warunkowego wyniesie co najwyżej 2k liczb, a całą sieć można określić za pomocą 2k liczb. Natomiast łączny rozkład zawiera liczby. Aby to uczynić konkretnym, załóżmy, że mamy n=30 węzłów, każdy z pięcioma rodzicami (k = 5). Następnie sieć bayesowska wymaga 960 numerów, ale pełna wspólna dystrybucja wymaga ponad miliarda.
Określenie tablic prawdopodobieństwa warunkowego dla w pełni połączonej sieci, w której każda zmienna ma wszystkich swoich poprzedników jako rodziców, wymaga takiej samej ilości informacji, jak określenie łącznego rozkładu w formie tabelarycznej. Z tego powodu często pomijamy łącza, mimo że istnieje niewielka zależność, ponieważ niewielki wzrost dokładności nie jest wart dodatkowej złożoności sieci. Na przykład, ktoś mógłby sprzeciwić się naszej sieci włamań, twierdząc, że jeśli nastąpi duże trzęsienie ziemi, to Jan i Maria nie zadzwonią, nawet gdyby usłyszeli alarm, ponieważ zakładają, że przyczyną jest trzęsienie ziemi. Czy dodać link z Earthquake do John Calls i Marry Calls(i w ten sposób powiększyć tabele) zależy od tego, jak ważne jest uzyskanie dokładniejszych prawdopodobieństw w porównaniu z kosztem określenia dodatkowych informacji. Nawet w domenie o strukturze lokalnej otrzymamy kompaktową sieć Bayes tylko wtedy, gdy wybierzemy uporządkowanie węzłów dobrze. Co się stanie, jeśli zdarzy nam się wybrać niewłaściwą kolejność? Rozważmy ponownie przykład włamania. Załóżmy, że decydujemy się dodać węzły w kolejności MarryCalls , JohnCalls , Alarm, Burglar, Earthquake. Wtedy stajemy się nieco bardziej skomplikowaną sieciąpokazana na rysunku (a) .
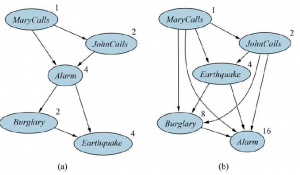
Proces przebiega następująco:
* Dodawanie MarryCalls: Brak rodziców.
* Dodanie JohnCalls: Jeśli Mary dzwoni, prawdopodobnie oznacza to, że włączył się alarm, co zwiększa prawdopodobieństwo, że Jan zadzwoni. Dlatego JohnCalls potrzebuje MarryCalls jako rodzica.
* Dodanie alarmu: Oczywiście, jeśli oboje dzwonią, jest bardziej prawdopodobne, że alarm włączył się, niż gdy tylko jeden lub żaden z nich nie dzwoni, więc jako rodzice potrzebujemy zarówno MarryCalls, jak i JohnCalls.
* Dodanie Włamywacza: Jeśli znamy stan alarmu, telefon od Jana lub Mary może dać nam informacje o dzwonku naszego telefonu lub muzyce Mary, ale nie o włamaniu:
![]()
Dlatego potrzebujemy tylko Alarm jako rodzica.
* Dodanie trzęsienia ziemi: Jeśli alarm jest włączony, jest bardziej prawdopodobne, że miało miejsce trzęsienie ziemi. (Alarm jest swego rodzaju wykrywaczem trzęsień ziemi.) Ale jeśli wiemy, że miało miejsce włamanie, to wyjaśnia to alarm, a prawdopodobieństwo trzęsienia ziemi byłoby tylko nieznacznie wyższe niż normalne. Dlatego jako rodzice potrzebujemy zarówno Alarmu, jak i Włamywacza.
Powstała sieć ma dwa łącza więcej niż oryginalna sieć na rysunku 13.2 i wymaga 13 prawdopodobieństw warunkowych zamiast 10. Co gorsza, niektóre łącza reprezentują wątłe relacje, które wymagają trudnych i nienaturalnych ocen prawdopodobieństwa, takich jak ocena prawdopodobieństwa trzęsienia ziemi, biorąc pod uwagę Włamywacz i alarm. Zjawisko to jest dość ogólne i wiąże się z wprowadzonym rozróżnieniem między modelami przyczynowymi i diagnostycznymi. Jeśli trzymamy się modelu przyczynowego, kończymy aby określić mniej liczb, a liczby będą często łatwiejsze do wymyślenia. Na przykład w dziedzinie medycyny Tversky i Kahneman wykazali, że doświadczeni lekarze wolą dokonywać ocen prawdopodobieństwa dla reguł przyczynowych niż diagnostycznych. Rysunek (b) pokazuje bardzo złą kolejność węzłów: MarryCalls, JohnCalls, Earthquake, Burglar, Alarm. Ta sieć wymaga określenia 31 różnych prawdopodobieństw — dokładnie tej samej liczby, co pełny wspólny rozkład. Należy jednak zdać sobie sprawę, że każda z trzech sieci może reprezentować dokładnie tę samą wspólną dystrybucję. Dwie wersje na rysunku po prostu nie reprezentują wszystkich warunkowych zależności niezależności i dlatego zamiast tego określają wiele niepotrzebnych liczb.