Równanie określa, co oznacza dana sieć Bayesa. Następnym krokiem jest wyjaśnienie, jak skonstruować sieć bayesowską w taki sposób, aby otrzymany wspólny rozkład był dobrą reprezentacją danej dziedziny. Pokażemy teraz, że równanie implikuje pewne warunkowe zależności niezależności, które mogą być wykorzystane do prowadzenia inżyniera wiedzy w konstruowaniu topologii sieci. Najpierw przepisujemy wpisy w łącznym rozkładzie pod kątem prawdopodobieństwa warunkowego, korzystając z reguły iloczynu
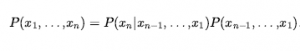
Następnie powtarzamy proces, redukując każde wspólne prawdopodobieństwo do prawdopodobieństwa warunkowego i łącznego prawdopodobieństwa dla mniejszego zestawu zmiennych. Kończymy z jednym dużym produktem:
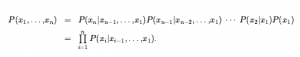
Ta tożsamość nazywana jest regułą łańcucha. Dotyczy to dowolnego zestawu zmiennych losowych. Porównując je z równaniem, widzimy, że specyfikacja łącznego rozkładu jest równoważna ogólnemu twierdzeniu, że dla każdej zmiennej Xi w sieci
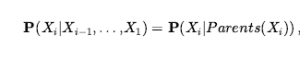
pod warunkiem że ![]()
Ten ostatni warunek spełnia numeracja
węzły w porządku topologicznym — to znaczy w dowolnej kolejności zgodnej ze strukturą grafu skierowanego. Na przykład węzły na rysunku 13.2 można uporządkować; B,E,A,J,M; E,B,A,M,J tak dalej.
Równanie mówi, że sieć bayesowska jest poprawną reprezentacją domeny tylko wtedy, gdy każdy węzeł jest warunkowo niezależny od swoich innych poprzedników w kolejności węzłów, biorąc pod uwagę jego rodziców. Możemy spełnić ten warunek za pomocą tej metodologii:
- WĘZŁY: Najpierw określ zestaw zmiennych, które są wymagane do modelowania domeny. Teraz uporządkuj je, {Xi,…,Xn} . Każde zamówienie będzie działać, ale powstała sieć będzie
być bardziej zwarty, jeśli zmienne są uporządkowane w taki sposób, że powodują efekty poprzedzające.
- LINKI: Dla i = 1 do n wykonaj:
* Wybierz minimalny zestaw rodziców dla Xi z X1,…Xi-1 , tak aby równanie (13.3) było spełnione
* Dla każdego rodzica wstaw link od rodzica do Xi .
* CPT: Zapisz tabelę prawdopodobieństwa warunkowego, ![]()
Intuicyjnie rodzice węzła Xi powinni zawierać wszystkie te węzły w Xi,…Xi-1, które bezpośrednio wpływają na Xi . Załóżmy na przykład, że ukończyliśmy sieć z wyjątkiem wyboru rodziców dla Marry Calls. Mary Calls jest z pewnością pod wpływem tego, czy ma miejsce włamywacz czy trzęsienie ziemi, ale nie ma na to bezpośredniego wpływu. Intuicyjnie, nasza wiedza o domenie mówi nam, że te wydarzenia wpływają na zachowanie Maryi tylko poprzez ich wpływ na alarm. Ponadto, biorąc pod uwagę stan alarmu, to, czy Jan dzwoni, nie ma wpływu na wołanie Marii. Formalnie uważamy, że następujące warunkowe oświadczenie o niezależności jest prawdziwe:
![]()
W ten sposób Alarm będzie jedynym węzłem nadrzędnym dla połączeń Marry Calls . Ponieważ każdy węzeł jest połączony tylko z wcześniejszymi węzłami, ta metoda budowy gwarantuje, że sieć jest acykliczna. Inną ważną właściwością sieci Bayesa jest to, że nie zawierają one zbędnych wartości prawdopodobieństwa. Jeśli nie ma redundancji, nie ma szans na niespójność: inżynier wiedzy lub ekspert domeny nie jest w stanie stworzyć sieci bayesowskiej, która narusza aksjomaty prawdopodobieństwa.