Semantyka sieci bayesowskich

Składnia sieci Bayesa składa się z skierowanego acyklicznego grafu z lokalnymi informacjami o prawdopodobieństwie dołączonymi do każdego węzła. Semantyka określa, w jaki sposób składnia odpowiada wspólnemu rozkładowi w zmiennych sieci. Załóżmy, że sieć Bayesa zawiera n zmiennych X₁,…,X_n . Ogólny wpis w dystrybucji sprzężenia to wtedy   lub w skrócie. Semantyka Sieci Bayesa definiuje każdy wpis we wspólnym rozkładzie w następujący sposób:

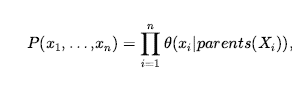
gdzie parents(Xi) oznacza wartości Parents(Xi), które pojawiają się w x1,…xn. Zatem każdy wpis w łącznym rozkładzie jest reprezentowany przez iloczyn odpowiednich elementów lokalnych rozkładów warunkowych w sieci Bayesa. Aby to zilustrować, możemy obliczyć prawdopodobieństwo, że zabrzmiał alarm, ale nie doszło do włamania ani trzęsienia ziemi, a Jan i Mary wołają. Po prostu mnożymy odpowiednie wpisy z lokalnych rozkładów warunkowych (skrót nazw zmiennych):

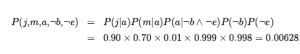
Wcześniej wyjaśniono, że pełną wspólną dystrybucję można wykorzystać do odpowiedzi na każde zapytanie dotyczące domeny. Jeśli sieć Bayesa jest reprezentacją łącznego rozkładu, to również może być użyta do odpowiedzi na dowolne zapytanie, poprzez zsumowanie wszystkich odpowiednich wspólnych wartości prawdopodobieństwa, z których każda jest obliczona przez pomnożenie prawdopodobieństw z lokalnych rozkładów warunkowych. Sekcja wyjaśnia to bardziej szczegółowo, ale opisuje również metody, które są znacznie wydajniejsze. Do tej pory przemilczeliśmy jeden ważny punkt: jakie znaczenie mają liczby wchodzące w lokalne rozkłady warunkowe theta(rodzice(Xi)? Okazuje się, że z równania  możemy udowodnić, że parametry teta(rodzice (Xi) to dokładnie prawdopodobieństwa warunkowe P(xi|rodzice(Xi)) implikowane przez łączny rozkład. Pamiętaj, że prawdopodobieństwa warunkowe można obliczyć z łącznego rozkładu w następujący sposób

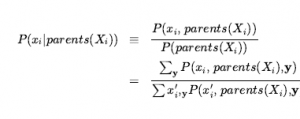
gdzie γ prezentuje wartości wszystkich zmiennych innych niż X_i i jego rodziców. Z tej ostatniej linii można to udowodnić . Stąd możemy przepisać równanie jako

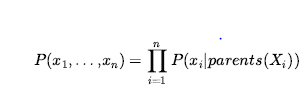
Oznacza to, że kiedy szacuje się wartości lokalnych rozkładów warunkowych, muszą one być rzeczywistymi prawdopodobieństwami warunkowymi dla zmiennej danej jej rodziców. Na przykład, gdy określimy powinno być tak, że około 90% czasu, gdy zabrzmi alarm, Jan dzwoni. Fakt, że każdy parametr sieci ma precyzyjne znaczenie tylko w postaci niewielkiego zestawu zmiennych, ma kluczowe znaczenie dla odporności i łatwości specyfikacji modeli.