Widzieliśmy, że pełny łączny rozkład prawdopodobieństwa może odpowiedzieć na każde pytanie dotyczące dziedziny, ale może stać się nieodwracalnie duży wraz ze wzrostem liczby zmiennych. Co więcej, określanie prawdopodobieństw dla światów możliwych jeden po drugim jest nienaturalne i nużące. Zobaczyliśmy również, że niezależność i warunkowa zależność niezależności między zmiennymi mogą znacznie zmniejszyć liczbę prawdopodobieństw, które należy określić, aby zdefiniować pełny łączny rozkład. Ta sekcja przedstawia strukturę danych zwaną siecią bayesowską, która reprezentuje zależności między zmiennymi. Sieci bayesowskie mogą przedstawiać zasadniczo dowolny pełny łączny rozkład prawdopodobieństwa iw wielu przypadkach mogą to robić w bardzo zwięzły sposób.
Sieć bayesowska to ukierunkowany graf, w którym każdy węzeł jest opisany ilościowymi informacjami o prawdopodobieństwie. Pełna specyfikacja przedstawia się następująco:
- Każdy węzeł odpowiada zmiennej losowej, która może być dyskretna lub ciągła.
- Skierowane łącza lub strzałki łączą pary węzłów. Jeśli istnieje strzałka od węzła X do węzła Y, mówi się, że X jest rodzicem Y. Wykres nie ma skierowanych cykli, a zatem jest skierowanym grafem acyklicznym lub DAG.
- Każdy węzeł Xi ma powiązaną informację o prawdopodobieństwie THETA(Xi|Parents(Xi)), która określa ilościowo wpływ rodziców na węzeł przy użyciu skończonej liczby parametrów.
Topologia sieci – zbiór węzłów i łączy – określa warunkowe relacje niezależności, które występują w domenie, w sposób, który zostanie wkrótce sprecyzowany. Intuicyjne znaczenie strzałki jest zazwyczaj takie, że X ma bezpośredni wpływ na Y, co sugeruje, że przyczyny powinny być rodzicami skutków. Ekspert dziedzinowy zazwyczaj łatwo jest zdecydować, jakie bezpośrednie wpływy istnieją w danej domenie – w rzeczywistości jest to o wiele łatwiejsze niż faktyczne określenie samych prawdopodobieństw. Po ułożeniu topologii sieci Bayesa na zewnątrz, musimy tylko określić lokalne informacje o prawdopodobieństwie dla każdej zmiennej, w postaci rozkładu warunkowego danego jej rodziców. Pełny łączny rozkład dla wszystkich zmiennych jest określony przez topologię i lokalne informacje o prawdopodobieństwie.
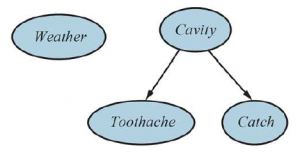
Przypomnij sobie prosty świat, składający się ze zmiennych Toothache, Cavity, Catch i Weather. Argumentowaliśmy, że Pogoda jest niezależna od innych zmiennych; ponadto argumentowaliśmy, że Toothache i Catch są warunkowo niezależne, biorąc pod uwagę Cavity. Relacje te są reprezentowane przez strukturę sieci Bayesa pokazaną na rysunku . Formalnie na warunkową niezależność Tothache i Catch, biorąc pod uwagę Catch, wskazuje brak powiązania między Tothache i Catch. Intuicyjnie sieć reprezentuje fakt, że Cavity jest bezpośrednią przyczyną Tootache i Catch, podczas gdy nie istnieje bezpośredni związek przyczynowy między Tootache i Catch.
Rozważmy teraz następujący przykład, który jest trochę bardziej złożony. Masz w domu zainstalowany nowy alarm antywłamaniowy. Jest dość niezawodny w wykrywaniu włamań, ale czasami jest wyzwalany przez drobne trzęsienia ziemi. (Ten przykład zawdzięczamy Judei Pearl, mieszkance podatnego na trzęsienia ziemi Los Angeles.) Masz również dwóch sąsiadów, Johna i Mary, którzy obiecali, że zadzwonią do ciebie do pracy, gdy usłyszą alarm. John prawie zawsze dzwoni, gdy słyszy alarm, ale czasami myli dzwoniący telefon z alarmem i dzwoni też wtedy. Z drugiej strony Mary lubi dość głośną muzykę i często zupełnie tęskni za alarmem. Mając dowody na to, kto dzwonił lub nie dzwonił, chcielibyśmy oszacować prawdopodobieństwo włamania. Sieć Bayesa dla tej domeny jest pokazana na rysunku. Struktura sieci pokazuje, że włamania i trzęsienia ziemi bezpośrednio wpływają na prawdopodobieństwo uruchomienia alarmu, ale to, czy zadzwoni Jan i Mary, zależy tylko od alarmu. Sieć reprezentuje więc nasze przypuszczenia, że nie dostrzegają włamań bezpośrednio, nie zauważają drobnych trzęsień ziemi, nie naradzają się przed wezwaniem.
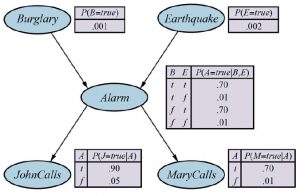
Informacje o lokalnym prawdopodobieństwie dołączone do każdego węzła na rysunku mają postać tabeli prawdopodobieństwa warunkowego (CPT). (CPT mogą być używane tylko dla zmiennych dyskretnych; inne reprezentacje, w tym te odpowiednie dla zmiennych ciągłych.) Każdy wiersz w CPT zawiera prawdopodobieństwo warunkowe każdej wartości węzła dla przypadku warunkowego. Przypadek warunkowania to tylko możliwa kombinacja wartości dla węzłów nadrzędnych – miniaturowy świat możliwych, jeśli chcesz. Każdy wiersz musi sumować się do 1, ponieważ wpisy reprezentują wyczerpujący zestaw obserwacji dla zmiennej. W przypadku zmiennych logicznych, gdy już wiesz, że prawdopodobieństwo wartości prawdziwej wynosi , prawdopodobieństwo fałszu musi wynosić 1-p , więc często pomijamy drugą liczbę, jak na rysunku 13.2 . Ogólnie rzecz biorąc, tabela dla zmiennej boolowskiej z k rodzicami boolowskimi zawiera 2k niezależnie określalnych prawdopodobieństw. Węzeł bez rodziców ma tylko jeden wiersz, reprezentujący wcześniejsze prawdopodobieństwa każdej możliwej wartości zmiennej.
Zauważ, że sieć nie ma węzłów odpowiadających temu, że Mary obecnie słucha głośnej muzyki lub telefonowi dzwoniącemu i zdezorientowanemu Johnowi. Czynniki te są podsumowane w niepewności związanej z powiązaniami Alarmu z Jhon Calls i Marry Calls. To pokazuje zarówno lenistwo, jak i ignorancję w działaniu. Byłoby dużo pracy, aby dowiedzieć się, dlaczego te czynniki byłyby bardziej lub mniej prawdopodobne w każdym konkretnym przypadku, a i tak nie mamy rozsądnego sposobu na uzyskanie odpowiednich informacji. Prawdopodobieństwo w rzeczywistości podsumowuje potencjalnie nieskończony zestaw okoliczności, w których alarm może nie zadziałać (wysoka wilgotność, awaria zasilania, rozładowana bateria, przecięte przewody, martwa mysz utknęła w dzwonku itp.) lub John lub Mary mogą nie zadziałać zadzwoń i zgłoś to (na obiad, na wakacje, chwilowo głuchy, przelatujący helikopter itp.). W ten sposób mały agent poradzi sobie z bardzo dużym światem, przynajmniej w przybliżeniu