Widzieliśmy, że reguła Bayesa może być przydatna do odpowiadania na pytania probabilistyczne uwarunkowane jednym dowodem – na przykład sztywnością karku. W szczególności argumentowaliśmy, że informacja probabilistyczna jest często dostępna w postaci P(efekt | przyczyna) . Co się dzieje, gdy mamy dwa lub więcej dowodów? Na przykład, co może wyciągnąć dentysta, jeśli jej paskudna stalowa sonda zaczepi się o bolący ząb pacjenta? Jeśli znamy pełny rozkład łączny , możemy odczytać odpowiedź:
![]()
Wiemy jednak, że takie podejście nie skaluje się do większej liczby zmiennych. Możemy spróbować użyć reguły Bayesa do przeformułowania problemu:

Aby to przeformułowanie zadziałało, musimy znać prawdopodobieństwa warunkowe połączenia tothache Λ catch dla każdej wartości Cavity . Może to być wykonalne dla zaledwie dwóch zmiennych dowodowych, ale znowu nie zwiększa się. Jeśli istnieje n możliwych zmiennych dowodowych (prześwietlenia, dieta, higiena jamy ustnej itp.), to istnieje O(2n) możliwych kombinacji obserwowanych wartości, dla których musielibyśmy znać prawdopodobieństwa warunkowe. Nie jest to lepsze niż korzystanie z pełnej dystrybucji łącznej. Aby zrobić postęp, musimy znaleźć dodatkowe twierdzenia dotyczące dziedziny, które pozwolą nam uprościć wyrażenia. Pojęcie niezależności dostarcza wskazówki, ale wymaga doprecyzowania. Byłoby miło, gdyby Toothach i Catch były niezależne, ale nie są: jeśli sonda zaczepi się o ząb, to prawdopodobnie ząb ma ubytek i ubytek powoduje ból zęba. Zmienne te są jednak niezależne, biorąc pod uwagę obecność lub brak wnęki. Każda z nich jest bezpośrednio spowodowana ubytkiem, ale żadna nie ma bezpośredniego wpływu na drugą: ból zęba zależy od stanu nerwów w zębie, natomiast dokładność sondy zależy przede wszystkim od umiejętności dentysty, dla którego ból zęba jest nieistotny. Matematycznie ta właściwość jest zapisana jako
![]()
Równanie to wyraża warunkową niezależność toothache i catch daego Cavity. Możemy to wstawić do równania, aby uzyskać prawdopodobieństwo Cavity:
![]()
Teraz wymagania informacyjne są takie same, jak w przypadku wnioskowania, przy czym każdy dowód jest używany oddzielnie: prawdopodobieństwo a priori P(Cavity) dla zmiennej zapytania oraz prawdopodobieństwo warunkowe każdego efektu, biorąc pod uwagę jego przyczynę. Ogólna definicja warunkowej niezależności dwóch zmiennych X i Y , przy danej trzeciej zmiennej Z, to
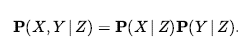
Na przykład w dziedzinie dentystycznej rozsądne wydaje się stwierdzenie warunkowej niezależności zmiennych Toothache i Catch , biorąc pod uwagę Cavity :
![]()
Zauważ, że to twierdzenie jest nieco silniejsze niż Equation (12.17) , które zapewnia niezależność tylko dla określonych wartości Toothache i Catch . Podobnie jak w przypadku absolutnej niezależności w Równaniu, równoważne formy
![]()
można również użyć. Sekcja wykazała, że twierdzenia o absolutnej niezależności pozwalają na rozkład pełnego wspólnego podziału na znacznie mniejsze części. Okazuje się, że to samo dotyczy warunkowych twierdzeń o niezależności. Na przykład, biorąc pod uwagę twierdzenie w Równaniu , możemy wyprowadzić dekompozycję w następujący sposób:
