Z pozoru reguła Bayesa nie wydaje się zbyt użyteczna. Pozwala nam obliczyć pojedynczy wyraz P(b|a) w postaci trzech wyrazów: P(a| b) ,P(b) i P(a) . Wydaje się, że to dwa kroki w tył; ale reguła Bayesa jest przydatna w praktyce, ponieważ w wielu przypadkach mamy dobre oszacowania prawdopodobieństwa dla tych trzech liczb i musimy obliczyć czwartą. Często postrzegamy jako dowód skutek jakiejś nieznanej przyczyny i chcielibyśmy tę przyczynę ustalić. W takim przypadku reguła Bayesa staje się
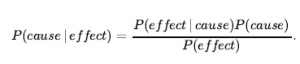
Prawdopodobieństwo warunkowe P(skutek | przyczyna) określa ilościowo zależność w kierunku przyczynowym, natomiast P(przyczyna | skutek) opisuje kierunek diagnostyczny. W zadaniu takim jak diagnoza medyczna często mamy warunkowe prawdopodobieństwa dotyczące związków przyczynowych. Lekarz zna P(objawy | choroba) i chce postawić diagnozę, P(choroba | objawy).
. Na przykład lekarz wie, że zapalenie opon mózgowych powoduje, że pacjent ma sztywność karku, powiedzmy, w 70% przypadków. Lekarz zna również pewne bezwarunkowe fakty: wcześniejsze prawdopodobieństwo, że którykolwiek pacjent ma zapalenie opon mózgowych wynosi 1/50 000, a wcześniejsze prawdopodobieństwo, że pacjent ma sztywność karku, wynosi 1%. Przyjmując propozycję, że pacjent ma sztywność karku, im propozycję, że pacjent ma zapalenie opon mózgowo-rdzeniowych, mamy

Oznacza to, że spodziewamy się, że tylko 0,14% pacjentów ze sztywnością karku będzie miało zapalenie opon mózgowych. Zauważ, że chociaż sztywność karku jest dość silnie wskazana przez zapalenie opon mózgowo-rdzeniowych (z prawdopodobieństwem 0,7), prawdopodobieństwo zapalenia opon mózgowych u pacjentów ze sztywnością karku pozostaje niewielkie. Dzieje się tak, ponieważ wcześniejsze prawdopodobieństwo sztywności karku (z jakiejkolwiek przyczyny) jest znacznie wyższe niż wcześniejsze w przypadku zapalenia opon mózgowych. Sekcja 12.3 zilustrowała proces, dzięki któremu można uniknąć oceny wcześniejszego prawdopodobieństwa, dowód (tutaj, P(s) ) poprzez obliczenie prawdopodobieństwa a posteriori dla każdej wartości zmiennej zapytania (tutaj, m i ¬m), a następnie znormalizowanie wyników. Ten sam proces można zastosować podczas korzystania z reguły Bayesa. Mamy
![]()
Tak więc, aby użyć tego podejścia, musimy oszacować P(s |¬m) zamiast P(s). Nie ma darmowego obiadu – czasem jest to łatwiejsze, czasem trudniejsze. Ogólna postać reguły Bayesa z normalizacją to
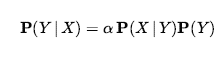
gdzie α jest stałą normalizacyjną potrzebną do zsumowania wpisów w P(Y|X) do 1. Jednym z oczywistych pytań, jakie należy zadać w związku z regułą Bayesa, jest to, dlaczego można mieć dostępne prawdopodobieństwo warunkowe w jednym kierunku, ale nie w drugim. Jeśli chodzi o zapalenie opon mózgowych, być może lekarz wie, że sztywność karku oznacza zapalenie opon mózgowych w 1 na 5000 przypadków; oznacza to, że lekarz ma informacje ilościowe w kierunku diagnostycznym od objawów do przyczyn. Taki lekarz nie musi stosować reguły Bayesa.
Niestety wiedza diagnostyczna jest często bardziej krucha niż wiedza przyczynowa. W przypadku nagłej epidemii zapalenia opon mózgowych bezwarunkowe prawdopodobieństwo wystąpienia zapalenia opon mózgowo-rdzeniowych, P(m), wzrośnie. Lekarz, który wyprowadził prawdopodobieństwo diagnostyczne P(m|s) bezpośrednio z obserwacji statystycznych pacjentów przed epidemią, nie będzie miał pojęcia, jak zaktualizować tę wartość, ale lekarz, który obliczy P(m|s) z pozostałych trzech wartości, zobaczy że P(m|s) powinno wzrosnąć proporcjonalnie do P(m) . Co najważniejsze, epidemia nie ma wpływu na informację o przyczynie P(s|m), ponieważ odzwierciedla ona po prostu sposób działania zapalenia opon mózgowych. Wykorzystanie tego rodzaju bezpośredniej wiedzy o przyczynach lub wiedzy opartej na modelach zapewnia kluczową odporność niezbędną, aby systemy probabilistyczne były wykonalne w świecie rzeczywistym.