Rozszerzmy pełny rozkład łączny na rysunku, dodając czwartą zmienną, Weather.
Pełny rozkład stawu staje się wtedy P(Toothache, Catch, Cavity, Weather), który ma 2x2x2x4=32 wpisy. Zawiera cztery „edycje” tabeli pokazanej na powyższym rysunku, po jednej dla każdego rodzaju pogody. Jaki związek mają te wydania ze sobą i z oryginalną tabelą trzech zmiennych? Jak ma się wartość P(toothache, catch, cavity, cloud) do wartości P(toothache, catch, cavity)? Możemy zastosować regułę produktu :

O ile nie zajmujemy się bóstwami, nie powinniśmy wyobrażać sobie, że problemy z zębami wpływają na pogodę. A przynajmniej w przypadku stomatologii w pomieszczeniach można bezpiecznie powiedzieć, że pogoda nie wpływa na zmienne uzębienia. Dlatego uzasadnione wydaje się następujące stwierdzenie:
![]()
Z tego możemy wywnioskować
![]()
Podobne równanie istnieje dla każdego wpisu w P(Ból zęba, Złap, Jamy, Pogoda) . W rzeczywistości możemy napisać ogólne równanie
![]()
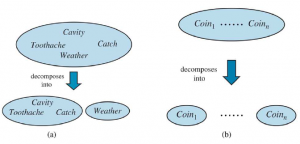
Tak więc tablicę 32-elementową dla czterech zmiennych można zbudować z jednej tabeli 8-elementowej i jednej tabeli 4-elementowej. Rozkład ten przedstawiono schematycznie na rysunku (a).
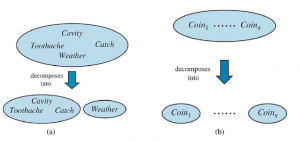
Własność, której użyliśmy w równaniu to niezależność (również niezależność marginalna i niezależność absolutna). W szczególności pogoda jest niezależna od Twojego problemu z zębami. Niezależność między zdaniami a i b można zapisać jako
![]()
Wszystkie te formy są równoważne. Niezależność między zmiennymi X i Y można zapisać w następujący sposób (ponownie wszystkie są równoważne):
![]()
Twierdzenia o niezależności są zwykle oparte na znajomości dziedziny. Jak pokazuje przykład bólu zęba – pogoda, mogą one radykalnie zmniejszyć ilość informacji niezbędnych do określenia pełnego rozmieszczenia stawów. Jeżeli cały zbiór zmiennych można podzielić na niezależne podzbiory, wówczas pełny łączny rozkład można rozłożyć na oddzielne łączne rozkłady na tych podzbiorach. Na przykład, pełny łączny rozkład wyniku n niezależnych rzutów monetą P(C1,…,Cn) ma 2n wpisów, ale można go przedstawić jako iloczyn n rozkładów pojedynczej zmiennej P(Ci). Mówiąc bardziej praktycznie, niezależność stomatologii i meteorologii jest dobrą rzeczą, ponieważ w przeciwnym razie praktyka dentystyczna może wymagać gruntownej znajomości meteorologii i na odwrót. Gdy są one dostępne, wówczas twierdzenia o niezależności mogą pomóc w zmniejszeniu rozmiaru reprezentacji domeny i złożoności problemu wnioskowania. Niestety, czyste oddzielenie całych zbiorów zmiennych przez niezależność jest dość rzadkie. Za każdym razem, gdy istnieje związek, jakkolwiek pośredni, między dwiema zmiennymi, niezależność nie zostanie utrzymana. Co więcej, nawet niezależne podzbiory mogą być dość duże – na przykład stomatologia może obejmować dziesiątki chorób i setki objawów, z których wszystkie są ze sobą powiązane. Aby poradzić sobie z takimi problemami, potrzebujemy bardziej subtelnych metod niż prosta koncepcja niezależności.