W tej sekcji opisujemy prostą metodę wnioskowania probabilistycznego – to jest obliczanie prawdopodobieństw a posteriori dla propozycji zapytań na podstawie zaobserwowanych dowodów. Pełną dystrybucję łączną wykorzystujemy jako „bazę wiedzy”, z której można uzyskać odpowiedzi na wszystkie pytania. Po drodze wprowadzamy również kilka przydatnych technik manipulowania równaniami obejmującymi prawdopodobieństwa. Zaczynamy od prostego przykładu: domeny składającej się tylko z trzech zmiennych logicznych Toothache, Cavity i Catch (paskudna stalowa sonda dentysty zaczepia się o mój ząb). Pełny rozkład połączeń wynosi 2 x 2 x 2 w tabeli, jak pokazano na rysunku

Zauważ, że prawdopodobieństwa w łącznym rozkładzie sumują się do 1, jak wymagają tego aksjomaty prawdopodobieństwa. Zauważ również, że Równanie daje nam bezpośredni sposób obliczania prawdopodobieństwa dowolnego zdania, prostego lub złożonego: po prostu zidentyfikuj te możliwe światy, w których zdanie jest prawdziwe i dodaj ich prawdopodobieństwa. Na przykład istnieje sześć możliwych światów, w których cavity V toothache utrzymuje:
![]()
Jednym ze szczególnie powszechnych zadań jest wyodrębnienie rozkładu dla pewnego podzbioru zmiennych lub pojedynczej zmiennej. Na przykład dodanie wpisów w pierwszym wierszu daje bezwarunkowe lub marginalne prawdopodobieństwo wystąpienia wgłębienia:
![]()
Proces ten nazywa się marginalizacją lub sumowaniem — ponieważ sumujemy prawdopodobieństwa dla każdej możliwej wartości innych zmiennych, tym samym usuwając je z równania. Dla dowolnych zbiorów zmiennych Y i Z możemy napisać następującą ogólną regułę marginalizacji:
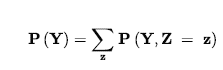
gdzie Σz sumuje wszystkie możliwe kombinacje wartości zbioru zmiennych Z. Jak zwykle możemy w tym równaniu skrócić P(Y,Z = z) przez P(Y,z). Dla przykładu Cavity, Equation odpowiada następującemu równaniu:

Korzystając z reguły iloczynu , możemy zastąpić P(Y,z) w równaniu przez P(Y|z)P(z) , otrzymując regułę zwaną warunkowaniem:
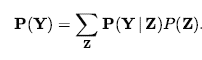
Marginalizacja i warunkowanie okazują się użytecznymi regułami dla wszelkiego rodzaju wyprowadzeń zawierających wyrażenia probabilistyczne. W większości przypadków interesuje nas obliczenie prawdopodobieństw warunkowych niektórych zmiennych, biorąc pod uwagę dowody dotyczące innych. Prawdopodobieństwa warunkowe można znaleźć, używając najpierw równania w celu uzyskania wyrażenia w kategoriach prawdopodobieństw bezwarunkowych, a następnie oceniając wyrażenie z pełnego rozkładu łącznego. Na przykład, możemy obliczyć prawdopodobieństwo ubytku, biorąc pod uwagę oznaki bólu zęba, w następujący sposób:

Aby to sprawdzić, możemy również obliczyć prawdopodobieństwo, że nie ma ubytku, biorąc pod uwagę ból zęba:

Obie wartości sumują się do 1,0, tak jak powinny. Zauważ, że mianownikiem obu tych obliczeń jest termin P (ból zęba). Gdyby zmienna Cavity miała więcej niż dwie wartości, byłaby w mianowniku dla nich wszystkich. W rzeczywistości można ją postrzegać jako stałą normalizacyjną dla rozkładu P (jamka | ból zęba), zapewniając, że sumuje się ona do 1. W rozdziałach dotyczących prawdopodobieństwa używamy α do oznaczania takich stałych. Za pomocą tego zapisu możemy zapisać dwa poprzednie równania w jednym:
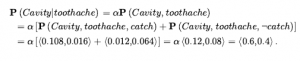
Innymi słowy, możemy obliczyć P(Jama | Ból zęba), nawet jeśli nie znamy wartości P(ból zęba)! Chwilowo zapominamy o współczynniku 1/P (ból zęba) i sumujemy wartości dla cavity i ¬cavity , otrzymując 0,12 i 0,08. To są prawidłowe proporcje względne, ale nie sumują się do 1, więc normalizujemy je dzieląc każdy przez 0,12 +0,08 , otrzymując prawdziwe prawdopodobieństwa 0,6 i 0,4. Normalizacja okazuje się przydatnym skrótem w wielu obliczeniach prawdopodobieństwa, zarówno w celu ułatwienia obliczeń, jak i umożliwienia nam kontynuacji, gdy niektóre oceny prawdopodobieństwa (takie jak P(ból zęba) ) nie są dostępne. Z przykładu możemy wyodrębnić ogólną procedurę wnioskowania. Zaczniemy od przypadku, w którym zapytanie obejmuje pojedynczą zmienną, X (w przykładzie Cavity). Niech E będzie listą zmiennych dowodowych (w przykładzie tylko Ból zęba), niech e będzie listą obserwowanych dla nich wartości, a Y będzie pozostałymi zmiennymi nieobserwowanymi (w przykładzie tylko Złap). Zapytanie to P(X|c) i może być ocenione jako
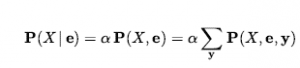
gdzie sumowanie obejmuje wszystkie możliwe y (tj. wszystkie możliwe kombinacje wartości nieobserwowanych zmiennych Y ). Zauważ, że razem zmienne X , E i Y tworzą kompletny zbiór zmiennych dla dziedziny, więc P(X,e,y) jest po prostu podzbiorem prawdopodobieństw z pełnego łącznego rozkładu. Biorąc pod uwagę pełny rozkład łączny do pracy, równanie (12.9) może odpowiadać na pytania probabilistyczne dla zmiennych dyskretnych. Nie skaluje się jednak dobrze: dla dziedziny opisanej przez n zmiennych logicznych, wymaga tabeli wejściowej o rozmiarze O(2n) i zajmuje czas O(2n) na przetworzenie tabeli. W realistycznym zadaniu moglibyśmy z łatwością mieć n = 100 , czyniąc O(2n) niepraktycznym – tabela z 2100 ≈ 1030 wpisami! Problemem nie jest tylko pamięć i obliczenia: prawdziwy problem polega na tym, że jeśli każde z 1030 prawdopodobieństw ma być oszacowane oddzielnie od przykładów, liczba wymaganych przykładów będzie astronomiczna. Z tych powodów pełny podział łączny w formie tabelarycznej rzadko jest praktycznym narzędziem do budowania systemów rozumowania. Zamiast tego należy ją postrzegać jako teoretyczną podstawę, na której można budować bardziej efektywne podejścia, podobnie jak tabele prawdy stanowiły teoretyczną podstawę dla bardziej praktycznych algorytmów, takich jak DPLL