Równania implikują pewne relacje między stopniami przekonań, które można przypisać logicznie powiązanym zdaniom. Na przykład możemy wyprowadzić znajomy związek między prawdopodobieństwem zdania a prawdopodobieństwem jego negacji:
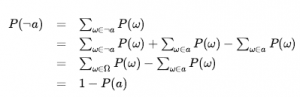
Możemy również wyprowadzić dobrze znany wzór na prawdopodobieństwo alternatywy, zwany czasem zasadą włączenia – wykluczenia:
![]()
Zasadę tę łatwo zapamiętać, zauważając, że przypadki, w których zachodzi, wraz z przypadkami, w których zachodzi, z pewnością obejmują wszystkie przypadki, w których zachodzi a V b; ale zsumowanie tych dwóch zbiorów przypadków liczy ich przecięcie dwukrotnie, więc musimy odjąć P (a Λ b).
Tego rodzaju pytanie było przedmiotem dziesięcioleci intensywnej debaty między zwolennikami wykorzystywania prawdopodobieństw jako jedynej uzasadnionej formy stopni wiary, a zwolennikami alternatywnych podejść. Jeden z argumentów przemawiających za aksjomatami prawdopodobieństwa, po raz pierwszy przedstawiony przez Bruno de Finetti w 1931 r., jest następujący: jeśli agent ma pewien stopień wiary w twierdzenie a , to agent powinien być w stanie określić szanse, przy których jest obojętny na postawić za lub przeciwko . Pomyśl o tym jako o grze między dwoma agentami: Agent 1 stwierdza: „moja wiara w zdarzenie a wynosi 0,4”. Agent 2 ma wtedy swobodę wyboru, czy postawić za, czy przeciwko stawkom, które są zgodne z określonym stopniem wiary. Oznacza to, że Agent 2 może zaakceptować zakład Agenta 1, że nastąpi awaria, oferując 6 USD przeciwko 4 USD Agenta 1. Lub Agent 2 może zaakceptować zakład Agenta 1, że wystąpi ¬a, oferując 4 USD przeciwko 6 USD Agenta 1. Następnie obserwujemy wynik , a kto ma rację, zbiera pieniądze. Jeśli czyjeś stopnie wiary nie odzwierciedlają dokładnie świata, można oczekiwać, że w dłuższej perspektywie straci pieniądze na rzecz przeciwnika, którego przekonania dokładniej odzwierciedlają stan świata. Twierdzenie De Finettiego nie dotyczy wyboru właściwych wartości dla poszczególnych prawdopodobieństw, ale wyboru wartości dla prawdopodobieństw logicznie powiązanych zdań: Jeśli Agent 1 wyraża zestaw stopni przekonań, które naruszają aksjomaty teorii prawdopodobieństwa, wówczas istnieje kombinacja zakłady Agenta 2, które gwarantują, że Agent 1 za każdym razem straci pieniądze. Załóżmy na przykład, że Agent 1 ma zestaw stopni wiary z równania . Rysunek pokazuje, że jeśli Agent 2 zdecyduje się postawić 4 USD na a , 3 USD na b i 2 USD na ¬(aVb) , to Agent 1 zawsze traci pieniądze, niezależnie od wyników a i b . Twierdzenie De Finettiego implikuje, że żaden racjonalny podmiot nie może mieć przekonań, które naruszają aksjomaty prawdopodobieństwa.

Jednym z powszechnych zarzutów wobec twierdzenia de Finettiego jest to, że ta gra w zakłady jest dość wymyślna. Na przykład, co się stanie, jeśli ktoś odmówi postawienia? Czy to kończy kłótnię? Odpowiedź brzmi: gra w zakłady jest abstrakcyjnym modelem sytuacji decyzyjnej, w której każdy agent jest nieuchronnie zaangażowany w każdym momencie. Każde działanie (w tym bezczynność) jest rodzajem zakładu, a każdy wynik może być postrzegany jako wypłata zakładu. Odmowa obstawiania jest jak odmawianie upłynięcia czasu. Wysunięto inne silne argumenty filozoficzne przemawiające za wykorzystaniem prawdopodobieństw, w szczególności argumenty Coxa (1946), Carnapa (1950) i Jaynesa (2003). Każdy z nich konstruuje zbiór aksjomatów do rozumowania ze stopniami przekonań: brak sprzeczności, zgodność ze zwykłą logiką (na przykład, jeśli wiara w A rośnie, to wiara w -A musi spaść) i tak dalej. Jedynym kontrowersyjnym aksjomatem jest to, że stopnie wiary muszą być liczbami lub przynajmniej zachowywać się jak liczby, ponieważ muszą być przechodnie (jeśli wiara w A jest większa niż wiara w B, która jest większa niż wiara w C, to wiara w A musi być większe niż C) i porównywalne (przekonanie w A musi być równe, większe lub mniejsze niż przekonanie w B ). Można wtedy udowodnić, że prawdopodobieństwo jest jedynym podejściem, które spełnia te aksjomaty. Jednak świat jest taki, jaki jest, praktyczne demonstracje czasami przemawiają głośniej niż dowody. Sukces systemów rozumowania opartych na teorii prawdopodobieństwa był znacznie skuteczniejszy niż argumenty filozoficzne w nawracaniu. Przyjrzymy się teraz, w jaki sposób aksjomaty można zastosować do wnioskowania.