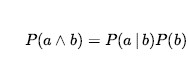Podobnie jak twierdzenia logiczne, twierdzenia probabilistyczne dotyczą światów możliwych. Podczas gdy twierdzenia logiczne mówią, które światy możliwe są ściśle wykluczone (wszystkie te, w których twierdzenie jest fałszywe), twierdzenia probabilistyczne mówią o prawdopodobieństwie różnych światów. W teorii prawdopodobieństwa zbiór wszystkich możliwych światów nazywamy przestrzenią prób. Światy możliwe wzajemnie się wykluczają i wyczerpują — dwa światy możliwe nie mogą mieć miejsca i jeden świat możliwy musi mieć miejsce. Na przykład, jeśli mamy rzucić dwiema (rozróżnialnymi) kośćmi, do rozważenia jest 36 możliwych światów: (1,1), (1,2), …, (6,6). Grecka litera Ω (wielka litera omega) odnosi się do przestrzeni próbki, a ω (mała litera omega) do elementów przestrzeni, czyli poszczególnych światów możliwych. W pełni określony model prawdopodobieństwa wiąże prawdopodobieństwo liczbowe P(ω) z każdym możliwym światem. Podstawowe aksjomaty teorii prawdopodobieństwa mówią, że każdy możliwy świat ma prawdopodobieństwo od 0 do 1, a całkowite prawdopodobieństwo zbioru możliwych światów wynosi 1:
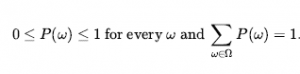
Na przykład, jeśli założymy, że każda kostka jest sprawiedliwa, a rzuty nie kolidują ze sobą, to każdy z możliwych światów (1,1), (1,2), …, (6,6) ma prawdopodobieństwo 1 /36 . Jeśli kostki zostaną załadowane, niektóre światy będą miały wyższe prawdopodobieństwa, a inne niższe, ale wszystkie nadal będą sumować się do 1. Probabilistyczne twierdzenia i zapytania zwykle nie dotyczą konkretnych światów możliwych, ale ich zbiorów. Na przykład możemy zapytać o prawdopodobieństwo, że obie kostki sumują się do 11, prawdopodobieństwo wyrzucenia podwojeń i tak dalej. W teorii prawdopodobieństwa zbiory te nazywa się zdarzeniami – termin ten był już szeroko stosowany w rozdziale 10 dla innego pojęcia. W logice zbiór światów odpowiada zdaniu w języku formalnym; konkretnie, dla każdego zdania, odpowiadający mu zbiór zawiera tylko te możliwe światy, w których to zdanie się zgadza. (Dlatego „zdarzenie” i „zdanie” oznaczają w tym kontekście mniej więcej to samo, z wyjątkiem tego, że zdanie jest wyrażone w języku formalnym.) Prawdopodobieństwo związane ze zdaniem definiuje się jako sumę prawdopodobieństw światów w które posiada:
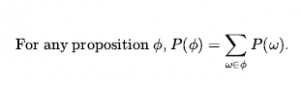
Na przykład, rzucając uczciwymi kośćmi, mamy P(TOTAL =11) = P((5,6))+ P((6,5)) = 1/36 + 1/36 =1/18 . Zauważ, że teoria prawdopodobieństwa nie wymaga pełnej wiedzy o prawdopodobieństwach każdego możliwego świata. Na przykład, jeśli wierzymy, że kostki spiskują w celu uzyskania tej samej liczby, możemy stwierdzić, że P(podwaja się) = 1/4, nie wiedząc, czy kostki wolą podwójne 6 od podwojenia 2. Podobnie jak w przypadku twierdzeń logicznych, to twierdzenie ogranicza podstawowe model prawdopodobieństwa bez pełnego jego określenia. Prawdopodobieństwa takie jak P(TOTAL = 11) i P(doubles) są nazywane bezwarunkowymi lub uprzednimi prawdopodobieństwami (a czasami po prostu „priory” w skrócie); odnoszą się do stopni wiary w twierdzenia przy braku innych informacji. Jednak przez większość czasu mamy pewne informacje, zwykle nazywane dowodami, które zostały już ujawnione. Na przykład pierwsza kostka może już wskazywać 5 i czekamy z zapartym tchem, aż druga przestanie się obracać. W takim przypadku nie interesuje nas bezwarunkowe prawdopodobieństwo wyrzucenia dubletu, ale prawdopodobieństwo warunkowe lub a posteriori (lub po prostu „a posteriori” w skrócie) wyrzucenia dubletu, biorąc pod uwagę, że pierwsza kostka to 5. To prawdopodobieństwo jest zapisane jako P(podwaja | Kość1 = 5), gdzie „|” jest wymawiane jako „dane”.
Podobnie, jeśli idę do dentysty na regularnie zaplanowaną kontrolę, wówczas interesujące może być prawdopodobieństwo a priori P(jamka) = 0,2; ale jeśli pójdę do dentysty, bo boli mnie ząb, liczy się prawdopodobieństwo warunkowe P(próchnica|ból zęba) = 0,6. Ważne jest, aby zrozumieć, że P (jamka) = 0,2 jest nadal ważne po zaobserwowaniu bólu zęba; to po prostu nie jest szczególnie przydatne. Przy podejmowaniu decyzji agent musi opierać się na wszystkich zaobserwowanych dowodach. Ważne jest również zrozumienie różnicy między warunkowaniem a implikacją logiczną. Twierdzenie, że P(próchnica|ból zęba) = 0,6 nie oznacza „Kiedy ból zęba jest prawdziwy, wywnioskuj, że ubytek jest prawdziwy z prawdopodobieństwem 0,6”, a raczej „Gdy ból zęba jest prawdziwy i nie mamy dalszych informacji, wywnioskuj, że ubytek jest prawdziwy z prawdopodobieństwo 0,6.” Dodatkowy warunek jest ważny; na przykład, gdybyśmy mieli dalsze informacje, że dentysta nie znalazł ubytków, zdecydowanie nie chcielibyśmy wnioskować, że ubytek jest prawdziwy z prawdopodobieństwem 0,6; zamiast tego musimy użyć
![]()
Mówiąc matematycznie, prawdopodobieństwa warunkowe definiuje się w kategoriach prawdopodobieństw bezwarunkowych w następujący sposób: dla dowolnych zdań a i b mamy
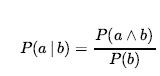
który posiada zawsze P(b) > 0 . Na przykład
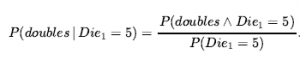
Definicja ma sens, jeśli pamiętasz, że obserwowanie b wyklucza wszystkie możliwe światy, w których b jest fałszywe, pozostawiając zbiór, którego całkowite prawdopodobieństwo wynosi tylko P(b) . W ramach tego zbioru światy, w których a jest prawdziwe, muszą spełniać a Λ b i stanowić ułamek P( aΛb) / P(b). Definicję prawdopodobieństwa warunkowego, można zapisać w innej postaci zwanej regułą iloczynu: