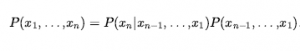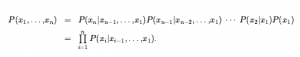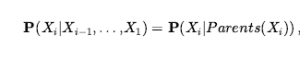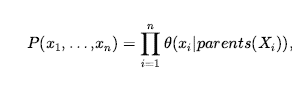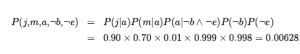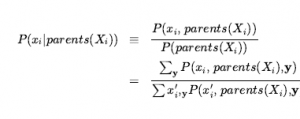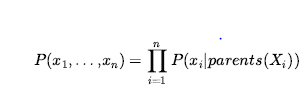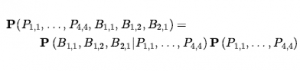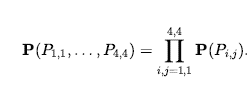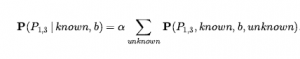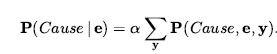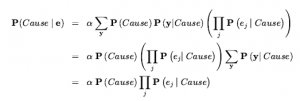Miesiąc: marzec 2022

Z semantyki sieci Bayesa zdefiniowanej w równaniu (13.2) możemy wyprowadzić szereg warunkowych własności niezależności. Widzieliśmy już właściwość, że zmienna jest warunkowo niezależna od swoich innych poprzedników, biorąc pod uwagę jej rodziców. Możliwe jest również udowodnienie bardziej ogólnej właściwości „niepotomnych”, że: Każda zmienna jest warunkowo niezależna od swoich niepotomków, biorąc pod uwagę jej rodziców. Na przykład na rysunku  zmienna JohnCalls jest niezależna od włamań, trzęsień ziemi i MarrryCalls, biorąc pod uwagę wartość Alarm. Definicja jest zilustrowana na rysunku  (a)

Okazuje się, że własność niepotomków w połączeniu z interpretacją parametrów sieci θ (Xi|Parents(Xi)) jako prawdopodobieństw warunkowych P(Xi|Parents(Xi)) wystarcza do odtworzenia pełnego wspólnego rozkładu podanego w równaniu (13.2) . Innymi słowy, można inaczej spojrzeć na semantykę sieci Bayesa: zamiast definiować pełny łączny rozkład jako iloczyn rozkładów warunkowych, sieć definiuje zbiór warunkowych własności niezależności. Na podstawie tych właściwości można wyprowadzić pełny rozkład połączeń. Inna ważna własność niezależności wynika z własności nie-potomków: zmienna jest warunkowo niezależna od wszystkich innych węzłów w sieci, biorąc pod uwagę jej rodziców, dzieci i rodziców dzieci – czyli biorąc pod uwagę jej koc Markowa.

Na przykład zmienna Burglary jest niezależna od JohnCalls i MaryCalls , biorąc pod uwagę Alarm i Earthquake. Ta właściwość jest zilustrowana na rysunku (b). Właściwość koca Markowa umożliwia algorytmy wnioskowania, które wykorzystują całkowicie lokalne i rozproszone procesy próbkowania stochastycznego.

Najbardziej ogólnym pytaniem o warunkową niezależność, jakie można zadać w sieci Bayesa, jest to, czy zbiór węzłów X jest warunkowo niezależny od innego zbioru Y, biorąc pod uwagę trzeci zbiór Z. Można to skutecznie określić, badając sieć Bayesa, aby zobaczyć, czy Z d-oddziela X i Y. Proces przebiega w następujący sposób:

1. Rozważmy tylko podwykres przodków składający się z X , Y , Z , i ich przodków.
2. Dodaj linki między dowolną niepołączoną parą węzłów, które mają wspólne dziecko; teraz mamy tak zwany wykres moralny.
3. Zastąp wszystkie linki skierowane linkami nieskierowanymi.
4. Jeśli Z blokuje wszystkie ścieżki pomiędzy X i Y w wynikowym wykresie, wtedy Z d oddziela X i Y . W takim przypadku X jest warunkowo niezależne od Y, biorąc pod uwagę Z . W przeciwnym razie oryginalna sieć Bayesa nie wymaga warunkowej niezależności.

Krótko mówiąc, d-separacja oznacza separację w nieukierunkowanym, moralizowanym podgrafie przodków. Stosując definicję do sieci włamaniowej z rysunku 13.2 możemy wywnioskować, że włamanie i trzęsienie ziemi są niezależne, biorąc pod uwagę pusty zbiór (tj. są całkowicie niezależne); że nie muszą być warunkowo niezależne w przypadku alarmu; oraz że JohnCalls i MarryCalls są warunkowo niezależne od danego Alarmu. Zauważ również, że właściwość koc Markowa wynika bezpośrednio z własności d-separation, ponieważ koc Markowa zmiennej d-oddziela ją od wszystkich innych zmiennych.

Oprócz tego, że jest kompletną i nieredundantną reprezentacją domeny, sieć Bayesa może często być znacznie bardziej zwarta niż pełna wspólna dystrybucja. Ta właściwość umożliwia obsługę domen z wieloma zmiennymi. Zwartość sieci bayesowskich jest przykładem ogólnej właściwości systemów o strukturze lokalnej (zwanych również rzadkimi). W systemie o strukturze lokalnej każdy podkomponent oddziałuje bezpośrednio tylko z ograniczoną liczbą innych komponentów, niezależnie od całkowitej liczby komponentów. Struktura lokalna jest zwykle kojarzona z liniowym, a nie wykładniczym wzrostem złożoności. W przypadku sieci Bayesa uzasadnione jest przypuszczenie, że w większości domen każda z nich jest losowa na zmienną bezpośrednio wpływają co najwyżej inne, dla niektórych stała k . Jeśli dla uproszczenia przyjmiemy n zmiennych logicznych, to ilość informacji potrzebnych do określenia każdej tabeli prawdopodobieństwa warunkowego wyniesie co najwyżej 2k liczb, a całą sieć można określić za pomocą 2k liczb. Natomiast łączny rozkład zawiera liczby. Aby to uczynić konkretnym, załóżmy, że mamy n=30 węzłów, każdy z pięcioma rodzicami (k = 5). Następnie sieć bayesowska wymaga 960 numerów, ale pełna wspólna dystrybucja wymaga ponad miliarda.

Określenie tablic prawdopodobieństwa warunkowego dla w pełni połączonej sieci, w której każda zmienna ma wszystkich swoich poprzedników jako rodziców, wymaga takiej samej ilości informacji, jak określenie łącznego rozkładu w formie tabelarycznej. Z tego powodu często pomijamy łącza, mimo że istnieje niewielka zależność, ponieważ niewielki wzrost dokładności nie jest wart dodatkowej złożoności sieci. Na przykład, ktoś mógłby sprzeciwić się naszej sieci włamań, twierdząc, że jeśli nastąpi duże trzęsienie ziemi, to Jan i Maria nie zadzwonią, nawet gdyby usłyszeli alarm, ponieważ zakładają, że przyczyną jest trzęsienie ziemi. Czy dodać link z Earthquake do John Calls i Marry Calls(i w ten sposób powiększyć tabele) zależy od tego, jak ważne jest uzyskanie dokładniejszych prawdopodobieństw w porównaniu z kosztem określenia dodatkowych informacji. Nawet w domenie o strukturze lokalnej otrzymamy kompaktową sieć Bayes tylko wtedy, gdy wybierzemy uporządkowanie węzłów dobrze. Co się stanie, jeśli zdarzy nam się wybrać niewłaściwą kolejność? Rozważmy ponownie przykład włamania. Załóżmy, że decydujemy się dodać węzły w kolejności MarryCalls , JohnCalls , Alarm, Burglar, Earthquake. Wtedy stajemy się nieco bardziej skomplikowaną sieciąpokazana na rysunku (a) .

Proces przebiega następująco:

* Dodawanie MarryCalls: Brak rodziców.

* Dodanie JohnCalls: Jeśli Mary dzwoni, prawdopodobnie oznacza to, że włączył się alarm, co zwiększa prawdopodobieństwo, że Jan zadzwoni. Dlatego JohnCalls potrzebuje MarryCalls jako rodzica.

* Dodanie alarmu: Oczywiście, jeśli oboje dzwonią, jest bardziej prawdopodobne, że alarm włączył się, niż gdy tylko jeden lub żaden z nich nie dzwoni, więc jako rodzice potrzebujemy zarówno MarryCalls, jak i JohnCalls.

* Dodanie Włamywacza: Jeśli znamy stan alarmu, telefon od Jana lub Mary może dać nam informacje o dzwonku naszego telefonu lub muzyce Mary, ale nie o włamaniu:

Dlatego potrzebujemy tylko Alarm jako rodzica.

* Dodanie trzęsienia ziemi: Jeśli alarm jest włączony, jest bardziej prawdopodobne, że miało miejsce trzęsienie ziemi. (Alarm jest swego rodzaju wykrywaczem trzęsień ziemi.) Ale jeśli wiemy, że miało miejsce włamanie, to wyjaśnia to alarm, a prawdopodobieństwo trzęsienia ziemi byłoby tylko nieznacznie wyższe niż normalne. Dlatego jako rodzice potrzebujemy zarówno Alarmu, jak i Włamywacza.

Powstała sieć ma dwa łącza więcej niż oryginalna sieć na rysunku 13.2 i wymaga 13 prawdopodobieństw warunkowych zamiast 10. Co gorsza, niektóre łącza reprezentują wątłe relacje, które wymagają trudnych i nienaturalnych ocen prawdopodobieństwa, takich jak ocena prawdopodobieństwa trzęsienia ziemi, biorąc pod uwagę Włamywacz i alarm. Zjawisko to jest dość ogólne i wiąże się z wprowadzonym rozróżnieniem między modelami przyczynowymi i diagnostycznymi. Jeśli trzymamy się modelu przyczynowego, kończymy aby określić mniej liczb, a liczby będą często łatwiejsze do wymyślenia. Na przykład w dziedzinie medycyny Tversky i Kahneman  wykazali, że doświadczeni lekarze wolą dokonywać ocen prawdopodobieństwa dla reguł przyczynowych niż diagnostycznych. Rysunek (b) pokazuje bardzo złą kolejność węzłów: MarryCalls, JohnCalls, Earthquake, Burglar, Alarm. Ta sieć wymaga określenia 31 różnych prawdopodobieństw — dokładnie tej samej liczby, co pełny wspólny rozkład. Należy jednak zdać sobie sprawę, że każda z trzech sieci może reprezentować dokładnie tę samą wspólną dystrybucję. Dwie wersje na rysunku po prostu nie reprezentują wszystkich warunkowych zależności niezależności i dlatego zamiast tego określają wiele niepotrzebnych liczb.

Równanie określa, co oznacza dana sieć Bayesa. Następnym krokiem jest wyjaśnienie, jak skonstruować sieć bayesowską w taki sposób, aby otrzymany wspólny rozkład był dobrą reprezentacją danej dziedziny. Pokażemy teraz, że równanie  implikuje pewne warunkowe zależności niezależności, które mogą być wykorzystane do prowadzenia inżyniera wiedzy w konstruowaniu topologii sieci. Najpierw przepisujemy wpisy w łącznym rozkładzie pod kątem prawdopodobieństwa warunkowego, korzystając z reguły iloczynu

Następnie powtarzamy proces, redukując każde wspólne prawdopodobieństwo do prawdopodobieństwa warunkowego i łącznego prawdopodobieństwa dla mniejszego zestawu zmiennych. Kończymy z jednym dużym produktem:

Ta tożsamość nazywana jest regułą łańcucha. Dotyczy to dowolnego zestawu zmiennych losowych. Porównując je z równaniem, widzimy, że specyfikacja łącznego rozkładu jest równoważna ogólnemu twierdzeniu, że dla każdej zmiennej X_i w sieci

pod warunkiem że

Ten ostatni warunek spełnia numeracja

węzły w porządku topologicznym — to znaczy w dowolnej kolejności zgodnej ze strukturą grafu skierowanego. Na przykład węzły na rysunku 13.2 można uporządkować; B,E,A,J,M; E,B,A,M,J  tak dalej.

Równanie mówi, że sieć bayesowska jest poprawną reprezentacją domeny tylko wtedy, gdy każdy węzeł jest warunkowo niezależny od swoich innych poprzedników w kolejności węzłów, biorąc pod uwagę jego rodziców. Możemy spełnić ten warunek za pomocą tej metodologii:

1. WĘZŁY: Najpierw określ zestaw zmiennych, które są wymagane do modelowania domeny. Teraz uporządkuj je, {Xi,…,Xn} . Każde zamówienie będzie działać, ale powstała sieć będzie

być bardziej zwarty, jeśli zmienne są uporządkowane w taki sposób, że powodują efekty poprzedzające.

2. LINKI: Dla i = 1 do n wykonaj:

* Wybierz minimalny zestaw rodziców dla Xi z X1,…Xi-1 , tak aby równanie (13.3) było spełnione

* Dla każdego rodzica wstaw link od rodzica do X_i .

* CPT: Zapisz tabelę prawdopodobieństwa warunkowego,

Intuicyjnie rodzice węzła Xi powinni zawierać wszystkie te węzły w Xi,…Xi-1, które bezpośrednio wpływają na Xi . Załóżmy na przykład, że ukończyliśmy sieć z wyjątkiem wyboru rodziców dla Marry Calls. Mary Calls jest z pewnością pod wpływem tego, czy ma miejsce włamywacz czy trzęsienie ziemi, ale nie ma na to bezpośredniego wpływu. Intuicyjnie, nasza wiedza o domenie mówi nam, że te wydarzenia wpływają na zachowanie Maryi tylko poprzez ich wpływ na alarm. Ponadto, biorąc pod uwagę stan alarmu, to, czy Jan dzwoni, nie ma wpływu na wołanie Marii. Formalnie uważamy, że następujące warunkowe oświadczenie o niezależności jest prawdziwe:

W ten sposób Alarm będzie jedynym węzłem nadrzędnym dla połączeń Marry Calls . Ponieważ każdy węzeł jest połączony tylko z wcześniejszymi węzłami, ta metoda budowy gwarantuje, że sieć jest acykliczna. Inną ważną właściwością sieci Bayesa jest to, że nie zawierają one zbędnych wartości prawdopodobieństwa. Jeśli nie ma redundancji, nie ma szans na niespójność: inżynier wiedzy lub ekspert domeny nie jest w stanie stworzyć sieci bayesowskiej, która narusza aksjomaty prawdopodobieństwa.

Składnia sieci Bayesa składa się z skierowanego acyklicznego grafu z lokalnymi informacjami o prawdopodobieństwie dołączonymi do każdego węzła. Semantyka określa, w jaki sposób składnia odpowiada wspólnemu rozkładowi w zmiennych sieci. Załóżmy, że sieć Bayesa zawiera n zmiennych X₁,…,X_n . Ogólny wpis w dystrybucji sprzężenia to wtedy   lub w skrócie. Semantyka Sieci Bayesa definiuje każdy wpis we wspólnym rozkładzie w następujący sposób:

gdzie parents(Xi) oznacza wartości Parents(Xi), które pojawiają się w x1,…xn. Zatem każdy wpis w łącznym rozkładzie jest reprezentowany przez iloczyn odpowiednich elementów lokalnych rozkładów warunkowych w sieci Bayesa. Aby to zilustrować, możemy obliczyć prawdopodobieństwo, że zabrzmiał alarm, ale nie doszło do włamania ani trzęsienia ziemi, a Jan i Mary wołają. Po prostu mnożymy odpowiednie wpisy z lokalnych rozkładów warunkowych (skrót nazw zmiennych):

Wcześniej wyjaśniono, że pełną wspólną dystrybucję można wykorzystać do odpowiedzi na każde zapytanie dotyczące domeny. Jeśli sieć Bayesa jest reprezentacją łącznego rozkładu, to również może być użyta do odpowiedzi na dowolne zapytanie, poprzez zsumowanie wszystkich odpowiednich wspólnych wartości prawdopodobieństwa, z których każda jest obliczona przez pomnożenie prawdopodobieństw z lokalnych rozkładów warunkowych. Sekcja wyjaśnia to bardziej szczegółowo, ale opisuje również metody, które są znacznie wydajniejsze. Do tej pory przemilczeliśmy jeden ważny punkt: jakie znaczenie mają liczby wchodzące w lokalne rozkłady warunkowe theta(rodzice(Xi)? Okazuje się, że z równania  możemy udowodnić, że parametry teta(rodzice (Xi) to dokładnie prawdopodobieństwa warunkowe P(xi|rodzice(Xi)) implikowane przez łączny rozkład. Pamiętaj, że prawdopodobieństwa warunkowe można obliczyć z łącznego rozkładu w następujący sposób

gdzie γ prezentuje wartości wszystkich zmiennych innych niż X_i i jego rodziców. Z tej ostatniej linii można to udowodnić . Stąd możemy przepisać równanie jako

Oznacza to, że kiedy szacuje się wartości lokalnych rozkładów warunkowych, muszą one być rzeczywistymi prawdopodobieństwami warunkowymi dla zmiennej danej jej rodziców. Na przykład, gdy określimy powinno być tak, że około 90% czasu, gdy zabrzmi alarm, Jan dzwoni. Fakt, że każdy parametr sieci ma precyzyjne znaczenie tylko w postaci niewielkiego zestawu zmiennych, ma kluczowe znaczenie dla odporności i łatwości specyfikacji modeli.

Widzieliśmy, że pełny łączny rozkład prawdopodobieństwa może odpowiedzieć na każde pytanie dotyczące dziedziny, ale może stać się nieodwracalnie duży wraz ze wzrostem liczby zmiennych. Co więcej, określanie prawdopodobieństw dla światów możliwych jeden po drugim jest nienaturalne i nużące. Zobaczyliśmy również, że niezależność i warunkowa zależność niezależności między zmiennymi mogą znacznie zmniejszyć liczbę prawdopodobieństw, które należy określić, aby zdefiniować pełny łączny rozkład. Ta sekcja przedstawia strukturę danych zwaną siecią bayesowską, która reprezentuje zależności między zmiennymi. Sieci bayesowskie mogą przedstawiać zasadniczo dowolny pełny łączny rozkład prawdopodobieństwa iw wielu przypadkach mogą to robić w bardzo zwięzły sposób.

Sieć bayesowska to ukierunkowany graf, w którym każdy węzeł jest opisany ilościowymi informacjami o prawdopodobieństwie. Pełna specyfikacja przedstawia się następująco:

1. Każdy węzeł odpowiada zmiennej losowej, która może być dyskretna lub ciągła.
2. Skierowane łącza lub strzałki łączą pary węzłów. Jeśli istnieje strzałka od węzła X do węzła Y, mówi się, że X jest rodzicem Y. Wykres nie ma skierowanych cykli, a zatem jest skierowanym grafem acyklicznym lub DAG.
3. Każdy węzeł Xi ma powiązaną informację o prawdopodobieństwie THETA(Xi|Parents(Xi)), która określa ilościowo wpływ rodziców na węzeł przy użyciu skończonej liczby parametrów.

Topologia sieci – zbiór węzłów i łączy – określa warunkowe relacje niezależności, które występują w domenie, w sposób, który zostanie wkrótce sprecyzowany. Intuicyjne znaczenie strzałki jest zazwyczaj takie, że X ma bezpośredni wpływ na Y, co sugeruje, że przyczyny powinny być rodzicami skutków. Ekspert dziedzinowy zazwyczaj łatwo jest zdecydować, jakie bezpośrednie wpływy istnieją w danej domenie – w rzeczywistości jest to o wiele łatwiejsze niż faktyczne określenie samych prawdopodobieństw. Po ułożeniu topologii sieci Bayesa na zewnątrz, musimy tylko określić lokalne informacje o prawdopodobieństwie dla każdej zmiennej, w postaci rozkładu warunkowego danego jej rodziców. Pełny łączny rozkład dla wszystkich zmiennych jest określony przez topologię i lokalne informacje o prawdopodobieństwie.

Przypomnij sobie prosty świat, składający się ze zmiennych Toothache, Cavity, Catch i Weather. Argumentowaliśmy, że Pogoda jest niezależna od innych zmiennych; ponadto argumentowaliśmy, że Toothache i Catch są warunkowo niezależne, biorąc pod uwagę Cavity. Relacje te są reprezentowane przez strukturę sieci Bayesa pokazaną na rysunku . Formalnie na warunkową niezależność Tothache i Catch, biorąc pod uwagę Catch, wskazuje brak powiązania między Tothache i Catch. Intuicyjnie sieć reprezentuje fakt, że Cavity jest bezpośrednią przyczyną Tootache i Catch, podczas gdy nie istnieje bezpośredni związek przyczynowy między Tootache i Catch.

Rozważmy teraz następujący przykład, który jest trochę bardziej złożony. Masz w domu zainstalowany nowy alarm antywłamaniowy. Jest dość niezawodny w wykrywaniu włamań, ale czasami jest wyzwalany przez drobne trzęsienia ziemi. (Ten przykład zawdzięczamy Judei Pearl, mieszkance podatnego na trzęsienia ziemi Los Angeles.) Masz również dwóch sąsiadów, Johna i Mary, którzy obiecali, że zadzwonią do ciebie do pracy, gdy usłyszą alarm. John prawie zawsze dzwoni, gdy słyszy alarm, ale czasami myli dzwoniący telefon z alarmem i dzwoni też wtedy. Z drugiej strony Mary lubi dość głośną muzykę i często zupełnie tęskni za alarmem. Mając dowody na to, kto dzwonił lub nie dzwonił, chcielibyśmy oszacować prawdopodobieństwo włamania. Sieć Bayesa dla tej domeny jest pokazana na rysunku. Struktura sieci pokazuje, że włamania i trzęsienia ziemi bezpośrednio wpływają na prawdopodobieństwo uruchomienia alarmu, ale to, czy zadzwoni Jan i Mary, zależy tylko od alarmu. Sieć reprezentuje więc nasze przypuszczenia, że ​​nie dostrzegają włamań bezpośrednio, nie zauważają drobnych trzęsień ziemi, nie naradzają się przed wezwaniem.

Informacje o lokalnym prawdopodobieństwie dołączone do każdego węzła na rysunku mają postać tabeli prawdopodobieństwa warunkowego (CPT). (CPT mogą być używane tylko dla zmiennych dyskretnych; inne reprezentacje, w tym te odpowiednie dla zmiennych ciągłych.) Każdy wiersz w CPT zawiera prawdopodobieństwo warunkowe każdej wartości węzła dla przypadku warunkowego. Przypadek warunkowania to tylko możliwa kombinacja wartości dla węzłów nadrzędnych – miniaturowy świat możliwych, jeśli chcesz. Każdy wiersz musi sumować się do 1, ponieważ wpisy reprezentują wyczerpujący zestaw obserwacji dla zmiennej. W przypadku zmiennych logicznych, gdy już wiesz, że prawdopodobieństwo wartości prawdziwej wynosi , prawdopodobieństwo fałszu musi wynosić 1-p , więc często pomijamy drugą liczbę, jak na rysunku 13.2 . Ogólnie rzecz biorąc, tabela dla zmiennej boolowskiej z k rodzicami boolowskimi zawiera 2^k niezależnie określalnych prawdopodobieństw. Węzeł bez rodziców ma tylko jeden wiersz, reprezentujący wcześniejsze prawdopodobieństwa każdej możliwej wartości zmiennej.

Zauważ, że sieć nie ma węzłów odpowiadających temu, że Mary obecnie słucha głośnej muzyki lub telefonowi dzwoniącemu i zdezorientowanemu Johnowi. Czynniki te są podsumowane w niepewności związanej z powiązaniami Alarmu z Jhon Calls i Marry Calls. To pokazuje zarówno lenistwo, jak i ignorancję w działaniu. Byłoby dużo pracy, aby dowiedzieć się, dlaczego te czynniki byłyby bardziej lub mniej prawdopodobne w każdym konkretnym przypadku, a i tak nie mamy rozsądnego sposobu na uzyskanie odpowiednich informacji. Prawdopodobieństwo w rzeczywistości podsumowuje potencjalnie nieskończony zestaw okoliczności, w których alarm może nie zadziałać (wysoka wilgotność, awaria zasilania, rozładowana bateria, przecięte przewody, martwa mysz utknęła w dzwonku itp.) lub John lub Mary mogą nie zadziałać zadzwoń i zgłoś to (na obiad, na wakacje, chwilowo głuchy, przelatujący helikopter itp.). W ten sposób mały agent poradzi sobie z bardzo dużym światem, przynajmniej w przybliżeniu

Wcześniej przedstawiono podstawowe elementy teorii prawdopodobieństwa i zwrócono uwagę na znaczenie zależności niezależności i warunkowej niezależności w upraszczaniu probabilistycznych reprezentacji świata. Ten rozdział przedstawia systematyczny sposób przedstawiania takich relacji w formie sieci bayesowskiej. Definiujemy składnię i semantykę tych sieci i pokazujemy, jak można je wykorzystać do uchwycenia niepewności w wiedzę,  w naturalny i efektywny sposób. Następnie pokazujemy, jak wnioskowanie probabilistyczne, chociaż w najgorszym przypadku niewykonalne obliczeniowo, można skutecznie przeprowadzić w wielu praktycznych sytuacjach. Opisujemy również różne algorytmy wnioskowania przybliżonego, które często mają zastosowanie, gdy wnioskowanie dokładne jest niewykonalne. Rozszerzymy podstawowe idee sieci bayesowskich na bardziej wyraziste języki formalne służące do definiowania modeli prawdopodobieństwa.

* Niepewność powstaje zarówno z powodu lenistwa, jak i ignorancji. Jest nieunikniony w złożonych, niedeterministycznych lub częściowo obserwowalnych środowiskach.

* Prawdopodobieństwa wyrażają niezdolność agenta do podjęcia ostatecznej decyzji dotyczącej prawdziwości zdania. Prawdopodobieństwa podsumowują przekonania agenta w odniesieniu do dowodów.

* Teoria decyzji łączy przekonania i pragnienia agenta, definiując najlepsze działanie jako takie, które maksymalizuje oczekiwaną użyteczność.

* Podstawowe stwierdzenia prawdopodobieństwa obejmują wcześniejsze lub bezwarunkowe prawdopodobieństwa oraz późniejsze lub warunkowe prawdopodobieństwa nad prostymi i złożonymi twierdzeniami.

* Aksjomaty prawdopodobieństwa ograniczają prawdopodobieństwa logicznie powiązanych zdań. Agent, który łamie aksjomaty, musi w niektórych przypadkach zachowywać się irracjonalnie.

* Pełny łączny rozkład prawdopodobieństwa określa prawdopodobieństwo każdego pełnego przypisania wartości do zmiennych losowych. Zwykle jest zbyt duży, aby go utworzyć lub użyć w swojej jawnej formie, ale gdy jest dostępny, można go użyć do odpowiedzi na zapytania, po prostu dodając

w górę wpisów dla możliwych światów odpowiadających propozycjom zapytania.

* Bezwzględna niezależność między podzbiorami zmiennych losowych pozwala na rozłożenie pełnego rozkładu łącznego na mniejsze rozkłady łączne, co znacznie zmniejsza jego złożoność.

* Reguła Bayesa umożliwia obliczenie nieznanych prawdopodobieństw ze znanych prawdopodobieństw warunkowych, zwykle w kierunku przyczynowym. Stosowanie reguły Bayesa z wieloma dowodami napotyka te same problemy ze skalowaniem, co pełny rozkład łączny.

* Warunkowa niezależność spowodowana bezpośrednimi związkami przyczynowymi w domenie pozwala na rozłożenie pełnego łącznego rozkładu na mniejsze, warunkowe rozkłady.

* Naiwny model Bayesa zakłada warunkową niezależność wszystkich zmiennych skutku, biorąc pod uwagę jedną zmienną przyczyny; jego rozmiar rośnie liniowo wraz z liczbą efektów.

* Agent wumpus-world może obliczyć prawdopodobieństwa dla nieobserwowanych aspektów świata, poprawiając w ten sposób decyzje czysto logicznego agenta. Warunkowa niezależność sprawia, że ​​te obliczenia są wykonalne.

Możemy połączyć pomysły zawarte w tym rozdziale, aby rozwiązać problemy z rozumowaniem probabilistycznym w świecie wumpusów. (Patrz rozdział 7, aby uzyskać pełny opis świata wumpusów.) W świecie wumpusów pojawia się niepewność, ponieważ czujniki agenta dostarczają tylko częściowe informacje o świecie. Na przykład Rysunek pokazuje sytuację, w której każdy z trzech nieodwiedzonych, ale osiągalnych kwadratów — [1,3], [2,2] i [3,1] — może zawierać dół. Czyste wnioskowanie logiczne nie może niczego wywnioskować na temat tego, który kwadrat jest najprawdopodobniej bezpieczny, więc agent logiczny może być zmuszony do losowego wyboru. Zobaczymy, że agent probabilistyczny może zrobić znacznie lepiej niż agent logiczny.

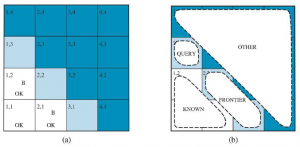
Naszym celem jest obliczenie prawdopodobieństwa, że każdy z trzech kwadratów zawiera dziurę. (W tym przykładzie ignorujemy wumpusa i złoto.) Odpowiednie właściwości świata wumpusa są takie, że (1) dziura wieje we wszystkich sąsiednich polach, oraz (2) każde pole inne niż [1,1] zawiera dół z prawdopodobieństwem 0,2. Pierwszym krokiem jest identyfikacja zestawu zmiennych losowych, których potrzebujemy:

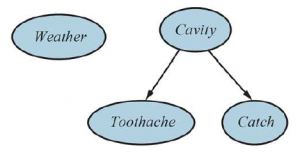
* Podobnie jak w przypadku logiki zdań, chcemy mieć jedną zmienną Boole’a Pij dla każdego kwadratu, co jest prawdziwe, jeśli kwadrat [i,j] faktycznie zawiera dołek.

* Mamy również zmienne logiczne Bij, które są prawdziwe, jeśli [i,j] square is breezy; uwzględniamy te zmienne tylko dla obserwowanych kwadratów — w tym przypadku [1,1], [1,2] i [2,1].

Następnym krokiem jest określenie pełnego rozkładu złącza, P(P1,1,…,P4,4, B1.1 ,…,B4,4).

Stosując regułę produktu, mamy

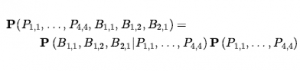
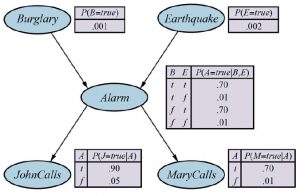
Ta dekompozycja ułatwia sprawdzenie, jakie powinny być wspólne wartości prawdopodobieństwa. Pierwszym terminem jest warunkowy rozkład prawdopodobieństwa konfiguracji bryzy, przy danej konfiguracji dołu; jego wartości wynoszą 1, jeśli wszystkie przewiewne kwadraty sąsiadują z dołami, a 0 w przeciwnym razie. Drugi termin to prawdopodobieństwo a priori konfiguracji dołu. Każdy kwadrat zawiera dołek z prawdopodobieństwem 0,2, niezależnie od pozostałych kwadratów; W związku z tym,

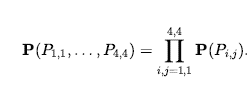
Dla konkretnej konfiguracji z dokładnie n dołkami prawdopodobieństwo wynosi 0,2ⁿ x 0,8^16-n. W sytuacji przedstawionej na rysunku dowodem jest zaobserwowana bryza (lub jej brak) na każdym odwiedzanym kwadracie, w połączeniu z faktem, że na każdym takim kwadracie nie ma jamy. Skrócimy te fakty jako b= ¬1,1 Λb1,2 Λ b2,1 i known = ¬p1,1 Λ ¬p_1,2 Λ ¬p2,1 . Interesują nas odpowiedzi na takie pytania jak P(P1,3 | known , b) : jakie jest prawdopodobieństwo, że [1,3] zawiera wgłębienie, biorąc pod uwagę dotychczasowe obserwacje? Aby odpowiedzieć na to zapytanie, możemy zastosować standardowe podejście równania , a mianowicie sumowanie wpisów z pełnego łącznego rozkładu. Niech Unknown będzie zbiorem zmiennych P_i,j dla kwadratów innych niż kwadraty znane i kwadrat zapytania [1,3]. Następnie z równania mamy

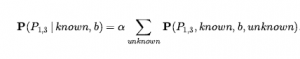
Podaliśmy już pełne prawdopodobieństwa łączne, więc gotowe – czyli chyba, że ​​zależy nam na obliczeniach. Jest 12 nieznanych kwadratów; stąd suma zawiera 2¹² = 4096 terminów. Ogólnie rzecz biorąc, sumowanie rośnie wykładniczo wraz z liczbą kwadratów. Zapewne ktoś mógłby zapytać, czy inne kwadraty nie są nieistotne? Jak [4,4] może wpłynąć na to, czy [1,3] ma dół? Rzeczywiście, ta intuicja jest z grubsza słuszna, ale trzeba ją doprecyzować. Tak naprawdę mamy na myśli to, że gdybyśmy znali wartości wszystkich zmiennych pit sąsiadujących z kwadratami, na których nam zależy, to doły (lub ich brak) w innych, bardziej odległych kwadratach nie miałyby dalszego wpływu na nasze przekonanie. Niech Frontier będzie zmiennymi pit (innymi niż zmienna zapytania), które sąsiadują z odwiedzonymi kwadratami, w tym przypadku tylko [2,2] i [3,1]. Niech również Other będzie zmiennymi pit dla innych nieznanych kwadratów; w tym przypadku jest 10 innych kwadratów, jak pokazano na rysunku (b). Z tymi definicjami Unknown = Frontier U Other . Kluczowe spostrzeżenie podane powyżej można teraz sformułować w następujący sposób: obserwowane bryzy są warunkowo niezależne od innych zmiennych, biorąc pod uwagę zmienne znane, graniczne i zapytania. Aby skorzystać z tego wglądu, manipulujemy formułą zapytania do postaci, w której bryza jest uwarunkowana wszystkimi innymi zmiennymi, a następnie stosujemy warunkową niezależność:

gdzie ostatni krok wykorzystuje warunkową niezależność: b jest niezależne od innych podanych znanych , P1,3 i granicy. Teraz pierwszy wyraz w tym wyrażeniu nie zależy od innych zmiennych, więc możemy przesunąć sumowanie do wewnątrz:

Przez niezależność, jak w Równaniu (12.22) , termin po prawej stronie może być rozłożony na czynniki, a następnie terminy mogą być uporządkowane:

gdzie ostatni krok składa P(known) w stałą normalizującą i wykorzystuje fakt ,że Σ_other jest równy 1.

Teraz w sumowaniu są tylko cztery wyrazy dla zmiennych granicznych P2,2 i P3,1 . Użycie niezależności i warunkowej niezależności całkowicie wyeliminowało inne kwadraty z rozważań.

Zauważ, że prawdopodobieństwa w P(b|k, P1,3, frontier) wynoszą 1, gdy obserwacje wiatru są zgodne z innymi zmiennymi i 0 w przeciwnym razie. Zatem dla każdej wartości P1,3 sumujemy modele logiczne dla zmiennych granicznych, które są zgodne z

znane fakty.  Modele i związane z nimi wcześniejsze prawdopodobieństwa — P(frontier) — pokazano na rysunku. Mamy

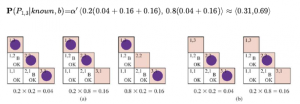
Oznacza to, że [1,3] (i [3,1] według symetrii) zawiera wgłębienie z prawdopodobieństwem około 31%. Podobne obliczenia, które czytelnik mógłby chcieć wykonać, pokazują, że [2,2] zawiera wgłębienie z około 86% prawdopodobieństwem. Agent wumpus powinien zdecydowanie unikać [2,2]! Zauważ, że nasz agent logiczny z rozdziału 7 nie wiedział, że [2,2] jest gorszy niż inne kwadraty. Logika może nam powiedzieć, że nie wiadomo, czy w [2, 2] jest dziura, ale potrzebujemy prawdopodobieństwa, aby powiedzieć nam, jakie to jest prawdopodobne. Ta sekcja pokazała, że ​​nawet pozornie skomplikowane problemy można precyzyjnie sformułować w teorii prawdopodobieństwa i rozwiązać za pomocą prostych algorytmów. Aby uzyskać wydajne rozwiązania, można wykorzystać niezależność i zależności warunkowe w celu uproszczenia wymaganych podsumowań. Te relacje często odpowiadają naszemu naturalnemu zrozumieniu, jak należy rozłożyć problem. W następnym rozdziale opracujemy formalne reprezentacje takich relacji, a także algorytmy operujące na tych reprezentacjach w celu efektywnego wnioskowania probabilistycznego.

Zobaczmy, jak naiwny model Bayesa można wykorzystać do zadania klasyfikacji tekstu: mając dany tekst, zdecyduj, do którego z predefiniowanego zestawu klas lub kategorii należy. Tutaj „przyczyną” jest zmienna Kategoria, a zmiennymi „skutek” jest obecność lub brak pewnych słów kluczowych, HasWord_i. Rozważ te dwa przykładowe zdania, zaczerpnięte z artykułów prasowych:

1. Akcje rosły w poniedziałek, a główne indeksy zyskały 1%, ponieważ optymizm utrzymywał się w sezonie wyników za pierwszy kwartał.
2. Ulewne deszcze nadal uderzały w większość wschodniego wybrzeża w poniedziałek, a ostrzeżenia o powodziach wydano w Nowym Jorku i innych miejscach.

Zadanie polega na zaklasyfikowaniu każdego zdania do Kategorii — głównych działów gazety: wiadomości, sportu, biznesu, pogody lub rozrywki. Naiwny model Bayesa składa się z prawdopodobieństw wcześniejszych P(Kategoria) i prawdopodobieństw warunkowych P(HasWord_i | Kategoria).

Dla każdej kategorii c , P(Categry = c) jest szacowane jako ułamek wszystkich wcześniej widzianych dokumentów należących do kategorii c . Na przykład, jeśli 9% artykułów dotyczy pogody, ustawiamy P(Category = wetaher) = 0,09 . Podobnie, P(HasWordi | Kategoria) jest szacowane jako ułamek dokumentów z każdej kategorii, które zawierają słowo i ; być może 37% artykułów o biznesie zawiera słowo , „akcje”, więc P(HawWord=prawda | Kategoria -=biznes) jest ustawione na 0,37.

Aby skategoryzować nowy dokument, sprawdzamy, które słowa kluczowe pojawiają się w dokumencie, a następnie stosujemy równanie , aby uzyskać rozkład prawdopodobieństwa a posteriori dla kategorii. Jeśli musimy przewidzieć tylko jedną kategorię, bierzemy tę o najwyższym prawdopodobieństwie a posteriori. Zauważ, że w tym zadaniu obserwowana jest każda zmienna efektu, ponieważ zawsze możemy stwierdzić, czy dane słowo pojawia się w dokumencie. Naiwny model Bayesa zakłada, że ​​słowa występują w dokumentach niezależnie, z częstotliwością określoną przez kategorię dokumentu. To założenie niezależności jest w praktyce wyraźnie naruszane. Na przykład wyrażenie „pierwszy kwartał” pojawia się częściej w artykułach biznesowych (lub sportowych), niż wynikałoby to z pomnożenia prawdopodobieństw „pierwszego” i „kwartalnego”. Naruszenie niezależności zwykle oznacza, że ​​ostateczny a posteriori prawdopodobieństwa będą znacznie bliższe 1 lub 0 niż powinny; innymi słowy, model jest zbyt pewny swoich przewidywań. Z drugiej strony, nawet przy tych błędach, ranking możliwych kategorii jest często dość dokładny. Modele Naive Bayes są szeroko stosowane do określania języka, wyszukiwania dokumentów, filtrowania spamu i innych zadań klasyfikacyjnych. W przypadku zadań takich jak diagnostyka medyczna, w których rzeczywiste wartości prawdopodobieństw a posteriori mają znaczenie – na przykład przy podejmowaniu decyzji o wykonaniu wyrostka robaczkowego – zazwyczaj woli się używać bardziej wyrafinowanych modeli.

Przykład stomatologii ilustruje powszechnie występujący wzorzec, w którym pojedyncza przyczyna bezpośrednio wpływa na szereg skutków, z których wszystkie są warunkowo niezależne od przyczyny. Pełny wspólny rozkład można zapisać jako

Taki rozkład prawdopodobieństwa nazywany jest naiwnym modelem Bayesa – „naiwnym”, ponieważ jest często stosowany (jako założenie upraszczające) w przypadkach, gdy zmienne „skutków” nie są ściśle niezależne ze względu na zmienną przyczyny. (Naiwny model Bayesa jest czasami nazywany klasyfikatorem bayesowskim, co skłoniło prawdziwych Bayesa do nazwania go idiotycznym modelem Bayesa). W praktyce naiwne systemy Bayesa często działają bardzo dobrze, nawet jeśli założenie warunkowej niezależności nie jest ściśle prawda. Aby użyć naiwnego modelu Bayesa, możemy zastosować równanie, aby uzyskać prawdopodobieństwo przyczyny przy pewnych zaobserwowanych efektach. Zaobserwowane efekty nazwijmy E = e , podczas gdy pozostałe zmienne efektu Y są nieobserwowane. Następnie można zastosować standardową metodę wnioskowania z rozkładu łącznego :

Następnie otrzymujemy

gdzie następuje ostatni wiersz, ponieważ suma nad y wynosi 1. Reinterpretacja tego równania słowami: dla każdej możliwej przyczyny pomnóż prawdopodobieństwo a priori przyczyny przez iloczyn prawdopodobieństw warunkowych zaobserwowanych skutków danej przyczyny; następnie znormalizuj wynik. Czas wykonania tego obliczenia jest liniowy pod względem liczby zaobserwowanych efektów i nie zależy od liczby nieobserwowanych efektów (która może być bardzo duża w dziedzinach takich jak medycyna). W następnym rozdziale zobaczymy, że jest to powszechne zjawisko we wnioskowaniu probabilistycznym: zmienne dowodowe, których wartości są nieobserwowane, zwykle „znikają” z obliczeń.