Miesiąc: styczeń 2022

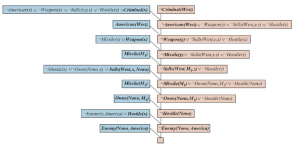
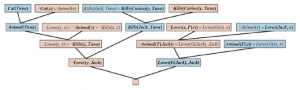
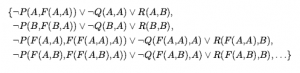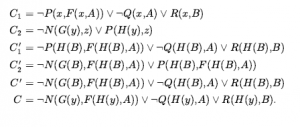Rozszerzając nieco język logiki pierwszego rzędu, aby uwzględnić matematyczny schemat indukcji w arytmetyce, Kurt Gödel był w stanie wykazać w swoim twierdzeniu o niezupełności, że istnieją prawdziwe zdania arytmetyczne, których nie można udowodnić. Dowód twierdzenia o niezupełności wykracza nieco poza zakres tej książki, zajmując co najmniej 30 stron, ale tutaj możemy dać wskazówkę. Zaczynamy od logicznej teorii liczb. W tej teorii istnieje pojedyncza stała 0 i pojedyncza funkcja S (funkcja następnika). W zamierzonym modelu S(0) oznacza 1, S(S(0)) oznacza 2 i tak dalej; język ma zatem nazwy dla wszystkich liczb naturalnych. Słownik zawiera również symbole funkcji + , x i Expt(potęgowanie) oraz zwykły zestaw spójników logicznych i kwantyfikatorów. Pierwszym krokiem jest zauważenie, że zbiór zdań, które możemy napisać w tym języku, można wyliczyć. (Wyobraźmy sobie zdefiniowanie porządku alfabetycznego na symbolach, a następnie ułożenie w porządku alfabetycznym każdego ze zbiorów zdań o długości 1, 2 itd.) Następnie możemy ponumerować każde zdanie α z unikalną liczbą naturalną #α (liczba Gödla). Ma to kluczowe znaczenie: teoria liczb zawiera nazwę dla każdego ze swoich własnych zdań. Podobnie możemy ponumerować każdy możliwy dowód P liczbą Gödla G(P) , ponieważ dowód jest po prostu skończonym ciągiem zdań. Załóżmy teraz, że mamy rekurencyjnie przeliczalny zbiór zdań A, które są prawdziwymi stwierdzeniami dotyczącymi liczb naturalnych. Przypominając, że A można nazwać za pomocą danego zbioru liczb całkowitych, możemy sobie wyobrazić napisanie w naszym języku zdania α(j,A) następującego rodzaju:

∀i   i nie jest liczbą Gödla dowodu zdania, którego liczbą Gödla jest j , gdzie dowód wykorzystuje tylko przesłanki w A

Następnie niech sigma; niech będzie zdanie alfa;(σA) , czyli zdanie, które stwierdza własną niedowodliwość na podstawie A . (To, że to zdanie zawsze istnieje, jest prawdziwe, ale nie do końca oczywiste).

Teraz przedstawiamy następujący pomysłowy argument: Załóżmy, że sigma; można udowodnić z A; następnie sigma; jest fałszywe (ponieważ sigma; mówi, że nie można tego udowodnić). Ale wtedy mamy fałszywe zdanie, które można udowodnić z A , więc A nie może składać się tylko ze zdań prawdziwych – a naruszenie naszego założenia. Dlatego sigma; nie da się udowodnić z A . Ale to jest właśnie sigma; sama twierdzi; stąd sigma; to prawdziwe zdanie.

Wykazaliśmy więc (z wyjątkiem 29 1/2 strony), że dla każdego zestawu zdań prawdziwych teorii liczb, a w szczególności zestawu podstawowych aksjomatów, istnieją inne zdania prawdziwe, których nie można udowodnić na podstawie tych aksjomatów. Ustala to między innymi, że nigdy nie możemy udowodnić wszystkich twierdzeń matematyki w ramach danego systemu aksjomatów. Oczywiście było to ważne odkrycie dla matematyki. Jego znaczenie dla sztucznej inteligencji było szeroko dyskutowane, poczynając od spekulacji samego Gödla

Ta sekcja zawiera dowód kompletności rozwiązania. Może być bezpiecznie pominięty przez tych, którzy są gotowi przyjąć ją na wiarę. Pokazujemy, że rozwiązanie jest obalające zupełne, co oznacza, że jeśli zbiór zdań jest niezadowalający, to rozwiązanie zawsze będzie w stanie wyprowadzić sprzeczność. Rozdzielczość nie może być użyta do wygenerowania wszystkich logicznych konsekwencji zbioru zdań, ale może być użyta do ustalenia, że dane zdanie jest zawarte w zbiorze zdań. Można go zatem wykorzystać do znalezienia wszystkich odpowiedzi na zadane pytanie Q(x) , udowadniając, że KB Λ ¬Q(x) jest ono niezadowalające.

Przyjmujemy, że każde zdanie w logice pierwszego rzędu (bez równości) może zostać przepisane jako zbiór klauzul w CNF. Można to udowodnić przez indukcję na formie zdania, używając zdań atomowych jako przypadku bazowego. Naszym celem jest zatem udowodnienie, co następuje: jeśli S jest to niespełniony zbiór klauzul, to zastosowanie skończonej liczby kroków rozstrzygnięcia do S przyniesie sprzeczność.

Nasz szkic dowodowy podąża za oryginalnym dowodem Robinsona z pewnymi uproszczeniami zaczerpniętymi z Genesereth i Nilsson. Podstawowa struktura dowodu jest następująca:

1. Po pierwsze, zauważamy, że jeśli S jest niespełniony, to istnieje określony zbiór podstawowych wystąpień zdań S o takim charakterze, że ten zbiór również jest niespełniony (twierdzenie Herbranda).
2. Następnie odwołujemy się do twierdzenia o rozstrzygnięciu w podstawie podanego w rozdziale 7, które stwierdza, że ​​rozstrzyganie zdaniowe jest kompletne dla zdań gruntowych.
3. Następnie używamy lematu unoszącego, aby pokazać, że dla każdego dowodu rozstrzygnięcia zdań przy użyciu zbioru zdań podstawowych istnieje odpowiedni dowód rozstrzygnięcia pierwszego rzędu wykorzystujący zdania pierwszego rzędu, z których otrzymano zdania podstawowe.

Aby wykonać pierwszy krok, potrzebujemy trzech nowych koncepcji:

* HERBRAND UNIVERSE: Jeśli S jest zbiorem klauzul, to H_S , uniwersum Herbranda  S , jest zbiorem wszystkich podstawowych terminów, które można skonstruować z następującego:

1. Symbole funkcji w S , jeśli istnieją.
2. Symbole stałe w S , jeśli istnieją; jeśli brak, to domyślny symbol stałej, S.

Na przykład, jeśli S zawiera tylko zdanie  to H_S jest następującym nieskończonym zbiorem terminów podstawowych:

{A,B,F(A,A),F(A,B),F(B,A),F(B,B),F(A,F(A,A)),…}.

* NASYCENIE: Jeśli S jest zbiorem klauzul i P jest zbiorem warunków podstawowych, to  P(S) , nasycenie  S względem P , jest zbiorem wszystkich klauzul podstawowych uzyskanych przez zastosowanie wszystkich możliwych zgodnych podstawień warunków podstawowych w P dla zmiennych w S .

* BAZA HERBRAND: Nasycenie zbioru klauzul S w odniesieniu do jego uniwersum Herbranda nosi nazwę bazy Herbrand , pisanej jako H_S(S) . Na przykład, jeśli S zawiera wyłącznie klauzulę podaną powyżej, to H_S(S) jest nieskończonym zbiorem klauzul

Definicje te pozwalają na sformułowanie formy twierdzenia Herbranda (Herbrand, 1930):

Jeśli zbiór klauzul jest niespełniony, to istnieje skończony podzbiór H_S(S), który również jest niespełniony.

Niech S’ będzie tym skończonym podzbiorem zdań podstawowych. Teraz możemy odwołać się do twierdzenia o rozdzielczości podstawowej (strona 228), aby pokazać, że zamknięcie rozdzielczości RC(S’) zawiera pustą klauzulę. Oznacza to, że uruchomienie rozwiązania zdań do zakończenia na S” wyprowadzi sprzeczność.

Teraz, gdy ustaliliśmy, że zawsze istnieje dowód rozdzielczości obejmujący jakiś skończony podzbiór bazy Herbranda z , następnym krokiem jest wykazanie, że istnieje dowód rozdzielczości wykorzystujący klauzule samego S, które niekoniecznie są klauzulami podstawowymi. Zaczynamy od rozważenia pojedynczego zastosowania zasady resolution. Robinson stwierdził ten lemat:

Niech C₁ i C₂ będą dwoma klauzulami bez wspólnych zmiennych, a C1′ i C2′ będą podstawowymi instancjami C1 i C2 . Jeśli C’ jest rezolwentą C1′ i C2′ , to istnieje klauzula C taka, że (1) C jest rezolwentą C1 i C2 oraz (2) C’ jest podstawową instancją C.

Nazywa się to lematem znoszącym, ponieważ przenosi krok dowodowy z klauzul podstawowych do ogólnych klauzul pierwszego rzędu. Aby udowodnić swój podstawowy lemat podnoszenia, Robinson musiał wymyślić unifikację i wyprowadzić wszystkie właściwości większości ogólnych unifikatorów. Zamiast powtarzać tutaj dowód, po prostu zilustrujemy lemat:

Widzimy, że rzeczywiście C’ jest podstawową instancją C . Ogólnie, aby C1’i C2′ miały jakiekolwiek rezolwenty, muszą być skonstruowane przez zastosowanie najpierw do C1 i C2 najbardziej ogólnego unifikatora pary komplementarnych literałów w C1 i C2 . Z lematu o podnoszeniu łatwo wyprowadzić podobne stwierdzenie o dowolnej kolejności zastosowań reguły rozstrzygania:

Dla każdej klauzuli C’ w zamknięciu rezolucji S’ istnieje klauzula C w zamknięciu rezolucji S taka, że ​​C’ jest podstawową instancją C, a wyprowadzenie C ma taką samą długość jak wyprowadzenie C’.

Z tego faktu wynika, że ​​jeżeli klauzula pusta pojawia się w zamknięciu rezolucji S’ , to musi ona również pojawić się w zamknięciu rezolucji S . Dzieje się tak, ponieważ pusta klauzula nie może być podstawową instancją żadnej innej klauzuli. Reasumując: pokazaliśmy, że jeśli S jest niespełnialne, to istnieje skończone wyprowadzenie pustej klauzuli za pomocą reguły rozwiązywania. Zniesienie dowodzenia twierdzeń z klauzul podstawowych do klauzul pierwszego rzędu zapewnia ogromny wzrost mocy. Ten wzrost wynika z faktu, że dowód pierwszego rzędu wymaga zmiennych instancji tylko w takim stopniu, w jakim jest to konieczne dla dowodu, podczas gdy metody klauzul podstawowych były wymagane do zbadania ogromnej liczby arbitralnych instancji.

Rozdzielczość dowodzi, że KB |= α, udowadniając, że KB Λ ¬α jest niezadowalająca — to znaczy wyprowadzając pustą klauzulę. Podejście algorytmiczne jest identyczne z przypadkiem zdaniowym opisanym na rysunku 7.13, więc nie musimy go tutaj powtarzać. Zamiast tego podajemy dwa przykładowe dowody. Pierwszy to przykład przestępstwa. Zdania w CNF są

Uwzględniamy również zanegowany cel ¬Criminal(West). Dowód rozdzielczości pokazano na rysunku

Zwróć uwagę na strukturę: pojedynczy „kręgosłup” rozpoczynający się od klauzuli celu, rozstrzygany na podstawie klauzul z bazy wiedzy, aż do wygenerowania pustej klauzuli. Jest to charakterystyczne dla rozwiązania opartego na bazach wiedzy o klauzulach Horn. W rzeczywistości zdania wzdłuż głównego kręgosłupa odpowiadają dokładnie kolejnym wartościom zmiennej goli w algorytmie tworzenia łańcucha wstecznego . Dzieje się tak dlatego, że zawsze wybieramy rozwiązanie za pomocą zdania, którego pozytywny dosłowny łączy się z najbardziej wysuniętym na lewo dosłownym zdaniem „bieżącego” na grzbiecie; to jest dokładnie to, co dzieje się w łańcuchu wstecznym. Tak więc łańcuch wsteczny jest tylko szczególnym przypadkiem rozwiązania z określoną strategią sterowania, aby zdecydować, które rozwiązanie wykonać w następnej kolejności.

Nasz drugi przykład wykorzystuje Skolemization i obejmuje klauzule, które nie są klauzulami określonymi. Powoduje to nieco bardziej złożoną strukturę dowodu. 

Każdy, kto kocha wszystkie zwierzęta, jest przez kogoś kochany.

Każdy, kto zabija zwierzę, nie jest przez nikogo kochany.

Jack kocha wszystkie zwierzęta.

Albo Jack, albo Curiosity zabili kota o imieniu Tuna.

Czy ciekawość zabiła kota?

Najpierw wyrażamy oryginalne zdania, pewną podstawową wiedzę i zanegowany cel G w logice pierwszego rzędu:

Teraz stosujemy procedurę konwersji, aby przekonwertować każde zdanie na CNF:

Dowód rozdzielczości, że Curiosity zabił kota, jest pokazany na rysunku

Dowód można sparafrazować w następujący sposób:

Załóżmy, że Curiosity nie zabił tuńczyka. Wiemy, że zrobili to Jack lub Curiosity; tak Jack musi mieć. Tuńczyk to kot, a koty to zwierzęta, więc tuńczyk jest zwierzęciem. Ponieważ nikt, kto zabija zwierzę, nie jest przez nikogo kochany, wiemy, że nikt nie kocha Jacka. Z drugiej strony Jack kocha wszystkie zwierzęta, więc ktoś go kocha; więc mamy sprzeczność. Dlatego Curiosity zabił kota.

Dowód odpowiada na pytanie „Czy ciekawość zabiła kota?” ale często chcemy zadawać bardziej ogólne pytania, takie jak „Kto zabił kota?” Rozwiązanie może to zrobić, ale uzyskanie odpowiedzi wymaga trochę więcej pracy. Celem jest który po zanegowaniu staje się w CNF. Powtarzając dowód z rysunku z nowym zanegowanym celem, otrzymujemy podobne drzewo dowodowe, ale z podstawieniem  {w/Curiosity} w jednym z kroków. Tak więc w tym przypadku ustalenie, kto zabił kota, jest tylko kwestią śledzenia powiązań dla zmiennych zapytania w dowodzie. Niestety, rozdzielczość może czasami dawać niekonstruktywne dowody na cele egzystencjalne, gdy wiemy, że zapytanie jest prawdziwe, ale nie ma unikalnego powiązania dla zmiennej.

Reguła rozstrzygania dla klauzul pierwszego rzędu jest po prostu zniesioną wersją reguły rozwiązywania zdań podanej na stronie 226. Dwie klauzule, które z założenia są znormalizowane oddzielnie, tak że nie mają wspólnych zmiennych, mogą zostać rozwiązane, jeśli zawierają komplementarne literały. Literały zdaniowe są komplementarne, jeśli jeden jest negacją drugiego; Literały pierwszego rzędu są komplementarne, jeśli jeden łączy się z negacją drugiego. Tak więc mamy

gdzie . Na przykład możemy rozwiązać dwie klauzule

eliminując dopełniające się literały  Loves (G(x),x) i ¬Loves(u,v) z unifikatorem

, wytworzyć klauzulę rezolucyjną

Ta reguła jest nazywana regułą rozwiązywania binarnego, ponieważ rozwiązuje dokładnie dwa literały. Sama reguła rozwiązywania binarnego nie daje pełnej procedury wnioskowania. Reguła pełnej rozdzielczości rozwiązuje podzbiory literałów w każdej klauzuli, które są unifikowalne. Alternatywnym podejściem jest rozszerzenie faktoringu – usunięcie zbędnych literałów – do przypadku pierwszego rzędu. Faktoring zdaniowy redukuje dwa literały do jednego, jeśli są identyczne; faktoring pierwszego rzędu redukuje dwa literały do jednego, jeśli są one unifikowalne. Unifikator musi być zastosowany do całej klauzuli. Połączenie rozdzielczości binarnej i faktoringu jest kompletne.

Pierwszym krokiem jest przekształcenie zdań w spójną formę normalną (CNF) — czyli koniunkcję klauzul, gdzie każda klauzula jest alternatywą literałów. W CNF literały mogą zawierać zmienne, co do których zakłada się, że są uniwersalnie kwantyfikowalne. Na przykład zdanie

staje się

Kluczem jest to, że każde zdanie logiki pierwszego rzędu może zostać przekształcone w inferencyjnie równoważne zdanie CNF. Zasadnicza różnica wynika z potrzeby wyeliminowania kwantyfikatorów egzystencjalnych. Zilustrujemy tę procedurę, tłumacząc zdanie „Każdy, kto kocha wszystkie zwierzęta, jest przez kogoś kochany” lub

Kroki są następujące:

* WYELIMINUJ IMPLIKACJE: Zamień P => Q na ¬P  Q . W przypadku naszego przykładowego zdania należy to zrobić dwukrotnie:

* MOVE ¬ INWARDS: Oprócz zwykłych reguł dla zanegowanych spójników, potrzebujemy reguł dla zanegowanych kwantyfikatorów. Tak więc mamy

Nasze zdanie przechodzi następujące przekształcenia:

Zwróć uwagę, jak uniwersalny kwantyfikator (  ) w założeniu implikacji stał się kwantyfikatorem egzystencjalnym. Teraz zdanie brzmi: „Albo jest jakieś zwierzę, które nie kocha xc, albo (jeśli tak nie jest) ktoś kocha x”. Oczywiście znaczenie pierwotnego zdania zostało zachowane.

* STANDARYZUJ ZMIENNE: Dla zdań takich jak które używają tej samej nazwy zmiennej dwukrotnie, zmień nazwę jednej ze zmiennych. Pozwala to uniknąć późniejszych nieporozumień, gdy odrzucimy kwantyfikatory. Tak więc mamy

* SKOLEMIZUJ: Skolemizacja to proces usuwania kwantyfikatorów egzystencjalnych przez eliminację. W prostym przypadku jest to tak, jak reguła egzystencjalnej instancji: przetłumacz  P(x)  na P(A), gdzie A jest nową stałą. Nie możemy jednak zastosować egzystencjalnego wystąpienia do naszego zdania powyżej, ponieważ nie pasuje ono do wzorca α; tylko części zdania pasują do wzorca. Jeśli ślepo zastosujemy regułę do dwóch pasujących części, które otrzymamy

co ma całkowicie błędne znaczenie: mówi, że każdy albo nie kocha konkretnego zwierzęcia A, albo jest kochany przez jakąś konkretną istotę. W rzeczywistości nasze pierwotne zdanie pozwala każdemu nie kochać innego zwierzęcia lub być kochanym przez inną osobę. Zatem chcemy, aby encje Skolema zależały od x:

Tutaj F i G są funkcjami Skolema. Ogólna zasada jest taka, że argumentami funkcji Skolema są wszystkie uniwersalnie kwantyfikowalne zmienne, w których zakresie występuje kwantyfikator egzystencjalny. Podobnie jak w przypadku egzystencjalnego wystąpienia, zdanie skolemizowane jest spełnialne dokładnie wtedy, gdy zdanie oryginalne jest spełnialne.

* DROP UNIVERSAL QUANTIFIERS: W tym momencie wszystkie pozostałe zmienne muszą być uniwersalnie kwantyfikowane. Dlatego nie tracimy żadnych informacji, jeśli opuścimy kwantyfikator:

* ROZPOCZĘCIE V NA  Λ:

Ten krok może również wymagać spłaszczenia zagnieżdżonych spójników i rozłączeń. Zdanie jest teraz w CNF i składa się z dwóch klauzul. Jest znacznie trudniejszy do odczytania niż oryginalne zdanie z implikacjami. (Może pomóc wyjaśnienie, że funkcja Skolema F(x) odnosi się do zwierzęcia potencjalnie niekochanego przez x , podczas gdy G(x) odnosi się do kogoś, kto może kochać x.) Na szczęście ludzie rzadko muszą patrzeć na zdania CNF – tłumaczenie proces jest łatwo zautomatyzowany

Ostatnia z naszych trzech rodzin systemów logicznych i jedyna, która działa w przypadku dowolnej bazy wiedzy, a nie tylko określonych klauzul, to rozdzielczość. widzieliśmy, że rozwiązywanie zdań jest kompletną procedurą wnioskowania dla logiki zdań; w tej sekcji rozszerzymy to na logikę pierwszego rzędu.

W naszej dyskusji na temat łączenia w przód pokazaliśmy, w jaki sposób problemy spełnienia ograniczeń (CSP) mogą być kodowane jako klauzule określone. Standardowy Prolog rozwiązuje takie problemy w dokładnie taki sam sposób, jak algorytm cofania . Ponieważ wycofywanie wylicza domeny zmiennych, działa tylko w przypadku dostawców CSP o skończonej domenie. W terminologii Prologu musi istnieć skończona liczba rozwiązań dla dowolnego celu z niezwiązanymi zmiennymi. (Na przykład problem kolorowania mapy, w którym każda zmienna może przybrać jeden z czterech różnych kolorów). CSP z nieskończoną domeną — na przykład ze zmiennymi o wartościach całkowitych lub rzeczywistych – wymagają zupełnie innych algorytmów, takich jak propagacja granic lub programowanie liniowe. Rozważmy następujący przykład. Definiujemy triangle(X,Y,Z) jako predykat, który obowiązuje, jeśli trzy argumenty są liczbami, które spełniają nierówność trójkąta:

Jeśli zapytamy Prologa o trójkąt zapytań (3,4,5), to się powiedzie. Z drugiej strony, jeśli zapytamy o trójkąt(3,4,Z), nie znajdziemy rozwiązania, ponieważ podcel nie może być obsłużony przez Prolog; nie możemy porównać wartości niezwiązanej z 0. Programowanie w logice z ograniczeniami (CLP) umożliwia ograniczanie zmiennych, a nie ograniczanie. Rozwiązanie CLP to najbardziej szczegółowy zestaw ograniczeń dotyczących zmiennych zapytania, który można uzyskać z bazy wiedzy. Na przykład rozwiązaniem zapytania o trójkąt(3,4,Z) jest ograniczenie 7 > Z > 1 . Standardowe programy logiczne są tylko szczególnym przypadkiem CLP, w którym ograniczenia rozwiązania muszą być ograniczeniami równości – to znaczy powiązaniami.

Systemy CLP zawierają różne algorytmy rozwiązywania ograniczeń dla ograniczeń dozwolonych w języku. Na przykład system, który dopuszcza liniowe nierówności na zmiennych o wartościach rzeczywistych, może zawierać algorytm programowania liniowego do rozwiązywania tych ograniczeń. Systemy CLP przyjmują również znacznie bardziej elastyczne podejście do rozwiązywania standardowych zapytań programowania logicznego. Na przykład, zamiast podążania w głąb, wstecz od lewej do prawej, mogą użyć dowolnego z bardziej wydajnych algorytmów omówionych w rozdziale 6 , w tym heurystycznego porządkowania koniunkcji, backjumpingu, warunkowania zestawu cięcia i tak dalej. Systemy CLP łączą zatem elementy algorytmów spełniania ograniczeń, programowania logicznego i dedukcyjnych baz danych. Zdefiniowano kilka systemów, które pozwalają programiście na większą kontrolę nad kolejnością wyszukiwania w celu wnioskowania. Język MRS pozwala programiście na pisanie metareguł w celu określenia, które koniunkty są wypróbowywane jako pierwsze. Użytkownik może napisać regułę mówiącą, że cel z najmniejszą liczbą zmiennych powinien zostać wypróbowany jako pierwszy lub może napisać reguły specyficzne dla domeny dla poszczególnych predykatów.

Prolog używa semantyki bazy danych, jak omówiono to w Rozdziale 8.2.8. Założenie unikalnych nazw mówi, że każda stała Prologu i każdy termin podstawowy odnosi się do odrębnego obiektu, a założenie o zamkniętym świecie mówi, że jedyne zdania, które są prawdziwe, to te, które wynikają z bazy wiedzy. Nie ma sposobu na stwierdzenie, że zdanie jest fałszywe w Prologu. To sprawia, że Prolog jest mniej wyrazisty niż logika pierwszego rzędu, ale jest to część tego, co sprawia, że Prolog jest bardziej wydajny i zwięzły. Rozważ następujące twierdzenia dotyczące niektórych ofert kursów:

Zgodnie z założeniem unikalnych nazw CS i EE są różne (podobnie jak 101, 102 i 106), co oznacza, że istnieją cztery różne kursy. Przy założeniu zamkniętego świata nie ma innych kursów, więc są dokładnie cztery kursy. Ale jeśli byłyby to twierdzenia w FOL, a nie w semantyce bazy danych, to wszystko, co moglibyśmy powiedzieć, to to, że jest gdzieś pomiędzy jednym a kursem nieskończoności. Dzieje się tak, ponieważ twierdzenia (w FOL) nie zaprzeczają możliwości, że oferowane są również inne niewymienione kursy, ani nie mówią, że wspomniane kursy różnią się od siebie. Gdybyśmy chcieli przetłumaczyć Równanie  na FOL, otrzymalibyśmy następujące zdanie:

Nazywa się to uzupełnieniem równania  . Wyraża w FOL ideę, że istnieją co najwyżej cztery kursy. Aby wyrazić w FOL ideę, że istnieją co najmniej cztery kursy, musimy napisać uzupełnienie predykatu równości:

Uzupełnienie jest przydatne do zrozumienia semantyki bazy danych, ale ze względów praktycznych, jeśli problem można opisać za pomocą semantyki bazy danych, bardziej efektywne jest rozumowanie za pomocą Prologa lub innego systemu semantyki bazy danych, niż tłumaczenie na FOL i rozumowanie z pełnym FOL dowód twierdzenia.

Przejdziemy teraz do pięty achillesowej Prologu: rozbieżności między wyszukiwaniem w głąb i drzewem wyszukiwania, które zawierają powtarzające się stany i nieskończone ścieżki. Rozważmy następujący program logiczny, który decyduje, czy istnieje ścieżka między dwoma punktami na grafie skierowanym:

Prosty wykres trójwęzłowy, opisany przez fakty link(a,b) i link(b,c), pokazano na rysunku (a)

. Za pomocą tego programu ścieżka zapytania (a,c) generuje drzewo dowodowe pokazane na rysunku (a)

Z drugiej strony, jeśli ułożymy dwie klauzule w kolejności

następnie Prolog podąża nieskończoną ścieżką pokazaną na rysunku 9.9(b). Prolog jest zatem niekompletny jako dowodzenie twierdzeń dla klauzul określonych – nawet dla programów Datalog, jak pokazuje ten przykład – ponieważ w przypadku niektórych baz wiedzy nie dowodzi zdań, które są z nimi związane. Zauważ, że ten problem nie dotyczy łączenia w przód: po wywnioskowaniu path(a,b), path(b,c) i path(a,c) łączenie w przód zatrzymuje się. Tworzenie łańcucha wstecznego na podstawie głębokości najpierw ma również problemy z nadmiarowymi obliczeniami. Na przykład podczas znajdowania ścieżki z A₁ do J₄ na rysunku (b) Prolog przeprowadza 877 wnioskowania, z których większość obejmuje znalezienie wszystkich możliwych ścieżek do węzłów, z których cel jest nieosiągalny. Jest to podobne do problemu powtarzającego się stanu . Całkowita ilość wnioskowania może być wykładnicza w liczbie generowanych faktów podstawowych. Jeśli zamiast tego zastosujemy łańcuchowanie w przód, można wygenerować co najwyżej n² path(X,Y) faktów łączących n węzłów. W przypadku problemu z rysunku (b) potrzebne są tylko 62 wnioski. Łączenie w przód w problemach wyszukiwania grafów jest przykładem programowania dynamicznego, w którym rozwiązania podproblemów są konstruowane przyrostowo z rozwiązań mniejszych podproblemów i są buforowane w celu uniknięcia ponownego przeliczenia. Podobny efekt możemy uzyskać w systemie łańcuchów wstecznych, z tą różnicą, że tutaj rozbijamy duże cele na mniejsze, zamiast je budować. Tak czy inaczej, przechowywanie wyników pośrednich w celu uniknięcia powielania jest kluczowe. Jest to podejście stosowane przez systemy programowania opartego na logice tabelarycznej, które wykorzystują wydajne mechanizmy przechowywania i wyszukiwania. Programowanie w logice tabelarycznej łączy ukierunkowanie na cel łączenia wstecz z wydajnością programowania dynamicznego w łańcuchu do przodu. Jest również kompletny dla baz wiedzy Datalog, co oznacza, że programista nie musi się martwić o nieskończone pętle. (Nadal można uzyskać nieskończoną pętlę z predykatami takimi jak ojciec(X,Y), które odnoszą się do potencjalnie nieograniczonej liczby obiektów.)

Programowanie logiczne to technologia, która zbliża się do urzeczywistnienia deklaratywnego ideału : systemy powinny być konstruowane poprzez wyrażanie wiedzy w języku formalnym, a problemy powinny być rozwiązywane poprzez uruchamianie procesów wnioskowania na tej wiedzy. Ideał podsumowuje równanie Roberta Kowalskiego:

Prolog jest najczęściej używanym językiem programowania logicznego. Jest używany głównie jako język szybkiego prototypowania i do zadań związanych z manipulacją symbolami, takich jak pisanie kompilatorów (Van Roy, 1990) i analizowanie języka naturalnego (Pereira i Warren, 1980). W Prologu napisano wiele systemów eksperckich dla dziedzin prawnych, medycznych, finansowych i innych. Programy prologowe to zestawy określonych klauzul zapisanych w notacji nieco innej niż standardowa logika pierwszego rzędu. Prolog używa wielkich liter dla zmiennych i małych dla stałych — przeciwieństwo naszej konwencji logiki. Przecinki oddzielają spójniki w zdaniu, a zdanie jest napisane „od tyłu” od tego, do czego jesteśmy przyzwyczajeni; zamiast A Λ B => C w Prologu mamy CF:- A ,B. Oto typowy przykład:

W Prologu notacja [E|L] oznacza listę, której pierwszym elementem jest E, a reszta to L. Oto program Prologa dla append(X,Y,Z), który się powiedzie, jeśli lista Z jest wynikiem dołączania list X i Y:

W języku angielskim klauzule te możemy odczytać jako (1) dołączając pustą listę, a lista Y tworzy tę samą listę Y, a (2) [A|Z] jest wynikiem dołączania [A|X] i Y, pod warunkiem, że Z jest wynikiem dołączania X i Y. W większości języków wysokiego poziomu możemy napisać podobną funkcję rekurencyjną, która opisuje sposób dołączania dwóch list. Definicja Prologu jest jednak potężniejsza, ponieważ opisuje relację, która zachodzi między trzema argumentami, a nie funkcję obliczoną z dwóch argumentów. Na przykład, możemy zapytać zapytanie append(X,Y,[1,2,3]): jakie dwie listy można dodać, aby dać [1,2,3]? Prolog zwraca nam rozwiązania

Wykonywanie programów Prologu odbywa się poprzez łańcuchowanie wsteczne w głąb, gdzie klauzule są testowane w kolejności, w jakiej są napisane w bazie wiedzy. Projekt Prologu to kompromis między deklaratywnością a wydajnością wykonania. Niektóre aspekty Prologu wykraczają poza standardowe logiczne wnioskowanie:

* Prolog używa semantyki bazy danych zamiast semantyki pierwszego rzędu, co jest widoczne w sposobie traktowania równości i negacji.

* Istnieje zestaw wbudowanych funkcji arytmetycznych. Literały używające tych symboli funkcji są „udowadniane” przez wykonanie kodu, a nie dalsze wnioskowanie. Na przykład, cel „X to 4 +3 ” udaje się, gdy X jest powiązane z 7. Z drugiej strony cel „5 to X + Y” nie powiedzie się, ponieważ wbudowane funkcje nie rozwiązują arbitralnego równania.

* Istnieją wbudowane predykaty, które po wykonaniu mają skutki uboczne. Należą do nich predykaty wejścia-wyjścia oraz predykaty asercji/wycofywania służące do modyfikowania bazy wiedzy. Takie predykaty nie mają odpowiednika w logice i mogą dawać mylące wyniki – na przykład, jeśli fakty są potwierdzone w gałęzi drzewa dowodowego, która ostatecznie zawodzi.

* Wystąpienie sprawdzenia jest pomijane w algorytmie unifikacji Prologu. Oznacza to, że można dokonać pewnych nierozsądnych wniosków; w praktyce prawie nigdy nie stanowią one problemu.

* Prolog używa wyszukiwania z łańcuchem wstecznym w głąb, bez sprawdzania nieskończonej rekurencji. Stwarza to użyteczny język programowania, który jest bardzo szybki, gdy jest używany prawidłowo, ale oznacza to, że niektóre programy, które wyglądają jak poprawna logika, nie zostaną zakończone.