Pomysł, że jeden obiekt może być częścią innego, jest znany. Czyjś nos jest częścią czyjejś głowy, Rumunia jest częścią Europy, a ten rozdział jest częścią tej książki. Używamy ogólnej relacji PartOf, aby powiedzieć, że jedna rzecz jest częścią innej. Obiekty można grupować w hierarchie PartOf, przypominające hierarchię Podzbioru:

Część relacji jest przechodnia i zwrotna; to jest,
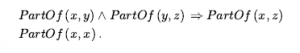
Dlatego możemy zawrzeć PartOf (Bukareszt, Ziemia). Kategorie obiektów złożonych często charakteryzują się strukturalnymi powiązaniami między częściami. Na przykład dwunożny to obiekt, który ma dokładnie dwie nogi przymocowane do ciała:
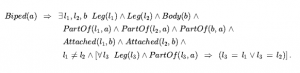
Notacja „dokładnie dwa” jest trochę niezręczna; jesteśmy zmuszeni powiedzieć, że istnieją dwie nogi, że nie są takie same i że jeśli ktoś proponuje trzecią, to musi być taka sama jak jedna z dwóch pozostałych.
Możemy zdefiniować relację PartPartition analogiczną do relacji Partition dla kategorii. Obiekt składa się z części w jego PartPartition i może być postrzegany jako pochodzący z niektórych właściwości z tych części. Na przykład masa obiektu złożonego jest sumą mas części. Zauważ, że tak nie jest w przypadku kategorii, które nie mają masy, nawet jeśli ich elementy mogą.
Przydatne jest również zdefiniowanie obiektów złożonych z określonymi częściami, ale bez określonej struktury. Na przykład możemy chcieć powiedzieć „Jabłka w tej torbie ważą dwa funty”. Pokusą byłoby przypisanie tej wagi do zbioru jabłek w torbie, ale byłoby to błędem, ponieważ zbiór jest abstrakcyjnym pojęciem matematycznym, które ma elementy, ale nie ma wagi. Zamiast tego potrzebujemy nowej koncepcji, którą nazwiemy wiązką. Na przykład, jeśli jabłka to Apple1, Appple2 i Apple3, to
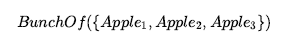
oznacza obiekt złożony z trzema jabłkami jako częściami (nie elementami). Możemy wtedy użyć wiązki jako normalnego, aczkolwiek nieustrukturyzowanego obiektu. Zauważ, że BunchOf({x}) = x . Ponadto BunchOf (jabłka) to złożony obiekt składający się ze wszystkich jabłek — nie należy mylić z jabłkami, kategorią lub zbiorem wszystkich jabłek. Możemy zdefiniować BunchOf w kategoriach relacji PartOf. Oczywiście każdy element jest częścią BunchOf (s):
![]()
Ponadto BunchOf (s) to najmniejszy obiekt spełniający ten warunek. Innymi słowy, BunchOf (s) musi być częścią dowolnego obiektu, który ma wszystkie elementy jako części:
![]()
Aksjomaty te są przykładem ogólnej techniki zwanej minimalizacją logiczną, która oznacza zdefiniowanie obiektu jako najmniejszego spełniającego określone warunki.