Organizacja obiektów w kategorie jest istotną częścią reprezentacji wiedzy. Chociaż interakcja ze światem odbywa się na poziomie pojedynczych obiektów, wiele rozumowań odbywa się na poziomie kategorii. Na przykład kupujący zwykle miałby na celu zakup piłki do koszykówki, a nie konkretnej piłki do koszykówki, takiej jak BB9 . Kategorie służą również do przewidywania obiektów po ich sklasyfikowaniu. Wnioskuje się obecność pewnych obiektów z danych wejściowych percepcyjnych, wnioskuje przynależność do kategorii na podstawie postrzeganych właściwości obiektów, a następnie wykorzystuje informacje o kategorii do przewidywania obiektów. Na przykład z zielonej i żółtej nakrapianej skóry, średnicy jednej stopy, jajowatego kształtu, czerwonego miąższu, czarnych nasion i obecności w alejce z owocami można wywnioskować, że przedmiot jest arbuzem; z tego wnioskuje się, że przydałby się do sałatek owocowych.
Istnieją dwie możliwości reprezentowania kategorii w logice pierwszego rzędu: predykaty i obiekty. Oznacza to, że możemy użyć predykatu Basketball(b) lub możemy zreifikować kategorię jako obiekt, Basketballs. Moglibyśmy wtedy powiedzieć Member(b,Basketballs), który będziemy skracać do b Basketalls, można powiedzieć, że b należy do kategorii piłek do koszykówki. Mówimy Subset(Basketballs,balls), w skrócie Basketballs Balls , aby powiedzieć, że Basketballs jest podkategorią Piłki. Podkategorii, podklasy i podzbioru będziemy używać zamiennie.
Kategorie porządkują wiedzę poprzez dziedziczenie. Jeśli powiemy, że wszystkie wystąpienia kategorii Żywność są jadalne i jeśli stwierdzimy, że Owoc jest podklasą Żywności, a Jabłka jest podklasą Owoców, możemy wywnioskować, że każde jabłko jest jadalne. Mówimy, że poszczególne jabłka dziedziczą właściwość jadalności, w tym przypadku z ich przynależności do kategorii Żywność. Relacje podklas organizują kategorie w hierarchię taksonomiczną lub taksonomię. Taksonomie były używane od wieków w dziedzinach technicznych. Największa taka taksonomia porządkuje około 10 milionów żyjących i wymarłych gatunków, z których wiele to chrząszcze, w jedną hierarchię; bibliotekoznawstwo opracowało taksonomię wszystkich dziedzin wiedzy, zakodowaną jako system dziesiętny Deweya; a organy podatkowe i inne departamenty rządowe opracowały obszerne taksonomie zawodów i produktów handlowych.
Logika pierwszego rzędu ułatwia określanie faktów na temat kategorii, czy to przez powiązanie obiektów z kategoriami, czy przez kwantyfikację ich elementów. Oto kilka przykładowych faktów:
* Obiekt jest członkiem kategorii.
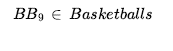
* Kategoria jest podklasą innej kategorii.
![]()
* Wszyscy członkowie kategorii mają pewne właściwości.
![]()
* Członkowie kategorii mogą być rozpoznawani przez niektóre właściwości.
![]()
* Kategoria jako całość ma pewne właściwości.
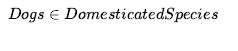
Zauważ, że ponieważ Pies jest kategorią i należy do Gatunków Udomowionych, ten ostatni musi być kategorią kategorii. Oczywiście są wyjątki od wielu z powyższych zasad (przebite piłki do koszykówki nie są sferyczne); tymi wyjątkami zajmiemy się później. Chociaż relacje podklas i składowych są najważniejsze dla kategorii, chcemy również móc określić relacje między kategoriami, które nie są podklasami względem siebie. Na przykład, jeśli po prostu powiemy, że studenci i studenci są podklasami Studentów, to nie powiedzieliśmy, że licencjat nie może być również studentem studiów magisterskich. Mówimy, że dwie lub więcej kategorii jest rozłącznych, jeśli nie mają wspólnych członków. Można też powiedzieć, że zajęcia licencjackie i magisterskie tworzą wyczerpujący rozkład studentów. Wyczerpujący rozkład zbiorów rozłącznych jest znany jako partycja. Oto kilka przykładów tych trzech koncepcji:

(Zauważ, że Wyczerpująca Dekompozycja Amerykanów Północnych nie jest podziałem, ponieważ niektórzy ludzie mają podwójne obywatelstwo.) Trzy predykaty są zdefiniowane w następujący sposób:
![]()
Kategorie mogą być również definiowane poprzez zapewnienie niezbędnych i wystarczających warunków członkostwa. Na przykład kawaler to nieżonaty dorosły mężczyzna:
![]()
Ścisłe logiczne definicje kategorii są zwykle możliwe tylko dla sztucznych terminów formalnych, a nie dla zwykłych obiektów. Ale definicje nie zawsze są potrzebne.