Rozdzielczość dowodzi, że KB |= α, udowadniając, że KB Λ ¬α jest niezadowalająca — to znaczy wyprowadzając pustą klauzulę. Podejście algorytmiczne jest identyczne z przypadkiem zdaniowym opisanym na rysunku 7.13, więc nie musimy go tutaj powtarzać. Zamiast tego podajemy dwa przykładowe dowody. Pierwszy to przykład przestępstwa. Zdania w CNF są
Uwzględniamy również zanegowany cel ¬Criminal(West). Dowód rozdzielczości pokazano na rysunku
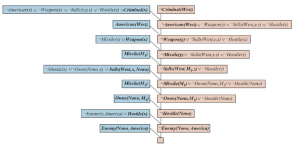
Zwróć uwagę na strukturę: pojedynczy „kręgosłup” rozpoczynający się od klauzuli celu, rozstrzygany na podstawie klauzul z bazy wiedzy, aż do wygenerowania pustej klauzuli. Jest to charakterystyczne dla rozwiązania opartego na bazach wiedzy o klauzulach Horn. W rzeczywistości zdania wzdłuż głównego kręgosłupa odpowiadają dokładnie kolejnym wartościom zmiennej goli w algorytmie tworzenia łańcucha wstecznego . Dzieje się tak dlatego, że zawsze wybieramy rozwiązanie za pomocą zdania, którego pozytywny dosłowny łączy się z najbardziej wysuniętym na lewo dosłownym zdaniem „bieżącego” na grzbiecie; to jest dokładnie to, co dzieje się w łańcuchu wstecznym. Tak więc łańcuch wsteczny jest tylko szczególnym przypadkiem rozwiązania z określoną strategią sterowania, aby zdecydować, które rozwiązanie wykonać w następnej kolejności.
Nasz drugi przykład wykorzystuje Skolemization i obejmuje klauzule, które nie są klauzulami określonymi. Powoduje to nieco bardziej złożoną strukturę dowodu.
Każdy, kto kocha wszystkie zwierzęta, jest przez kogoś kochany.
Każdy, kto zabija zwierzę, nie jest przez nikogo kochany.
Jack kocha wszystkie zwierzęta.
Albo Jack, albo Curiosity zabili kota o imieniu Tuna.
Czy ciekawość zabiła kota?
Najpierw wyrażamy oryginalne zdania, pewną podstawową wiedzę i zanegowany cel G w logice pierwszego rzędu:
Teraz stosujemy procedurę konwersji, aby przekonwertować każde zdanie na CNF:
Dowód rozdzielczości, że Curiosity zabił kota, jest pokazany na rysunku
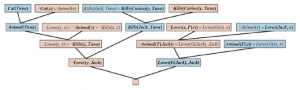
Dowód można sparafrazować w następujący sposób:
Załóżmy, że Curiosity nie zabił tuńczyka. Wiemy, że zrobili to Jack lub Curiosity; tak Jack musi mieć. Tuńczyk to kot, a koty to zwierzęta, więc tuńczyk jest zwierzęciem. Ponieważ nikt, kto zabija zwierzę, nie jest przez nikogo kochany, wiemy, że nikt nie kocha Jacka. Z drugiej strony Jack kocha wszystkie zwierzęta, więc ktoś go kocha; więc mamy sprzeczność. Dlatego Curiosity zabił kota.
Dowód odpowiada na pytanie „Czy ciekawość zabiła kota?” ale często chcemy zadawać bardziej ogólne pytania, takie jak „Kto zabił kota?” Rozwiązanie może to zrobić, ale uzyskanie odpowiedzi wymaga trochę więcej pracy. Celem jest 
który po zanegowaniu staje się 
w CNF. Powtarzając dowód z rysunku z nowym zanegowanym celem, otrzymujemy podobne drzewo dowodowe, ale z podstawieniem {w/Curiosity} w jednym z kroków. Tak więc w tym przypadku ustalenie, kto zabił kota, jest tylko kwestią śledzenia powiązań dla zmiennych zapytania w dowodzie. Niestety, rozdzielczość może czasami dawać niekonstruktywne dowody na cele egzystencjalne, gdy wiemy, że zapytanie jest prawdziwe, ale nie ma unikalnego powiązania dla zmiennej.