Pierwszym krokiem jest przekształcenie zdań w spójną formę normalną (CNF) — czyli koniunkcję klauzul, gdzie każda klauzula jest alternatywą literałów. W CNF literały mogą zawierać zmienne, co do których zakłada się, że są uniwersalnie kwantyfikowalne. Na przykład zdanie
staje się
Kluczem jest to, że każde zdanie logiki pierwszego rzędu może zostać przekształcone w inferencyjnie równoważne zdanie CNF. Zasadnicza różnica wynika z potrzeby wyeliminowania kwantyfikatorów egzystencjalnych. Zilustrujemy tę procedurę, tłumacząc zdanie „Każdy, kto kocha wszystkie zwierzęta, jest przez kogoś kochany” lub
Kroki są następujące:
* WYELIMINUJ IMPLIKACJE: Zamień P => Q na ¬P Q . W przypadku naszego przykładowego zdania należy to zrobić dwukrotnie:
* MOVE ¬ INWARDS: Oprócz zwykłych reguł dla zanegowanych spójników, potrzebujemy reguł dla zanegowanych kwantyfikatorów. Tak więc mamy
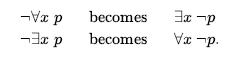
Nasze zdanie przechodzi następujące przekształcenia:
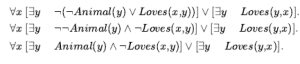
Zwróć uwagę, jak uniwersalny kwantyfikator ( ) w założeniu implikacji stał się kwantyfikatorem egzystencjalnym. Teraz zdanie brzmi: „Albo jest jakieś zwierzę, które nie kocha xc, albo (jeśli tak nie jest) ktoś kocha x”. Oczywiście znaczenie pierwotnego zdania zostało zachowane.
* STANDARYZUJ ZMIENNE: Dla zdań takich jak 
które używają tej samej nazwy zmiennej dwukrotnie, zmień nazwę jednej ze zmiennych. Pozwala to uniknąć późniejszych nieporozumień, gdy odrzucimy kwantyfikatory. Tak więc mamy
* SKOLEMIZUJ: Skolemizacja to proces usuwania kwantyfikatorów egzystencjalnych przez eliminację. W prostym przypadku jest to tak, jak reguła egzystencjalnej instancji: przetłumacz P(x) na P(A), gdzie A jest nową stałą. Nie możemy jednak zastosować egzystencjalnego wystąpienia do naszego zdania powyżej, ponieważ nie pasuje ono do wzorca α; tylko części zdania pasują do wzorca. Jeśli ślepo zastosujemy regułę do dwóch pasujących części, które otrzymamy
co ma całkowicie błędne znaczenie: mówi, że każdy albo nie kocha konkretnego zwierzęcia A, albo jest kochany przez jakąś konkretną istotę. W rzeczywistości nasze pierwotne zdanie pozwala każdemu nie kochać innego zwierzęcia lub być kochanym przez inną osobę. Zatem chcemy, aby encje Skolema zależały od x:
Tutaj F i G są funkcjami Skolema. Ogólna zasada jest taka, że argumentami funkcji Skolema są wszystkie uniwersalnie kwantyfikowalne zmienne, w których zakresie występuje kwantyfikator egzystencjalny. Podobnie jak w przypadku egzystencjalnego wystąpienia, zdanie skolemizowane jest spełnialne dokładnie wtedy, gdy zdanie oryginalne jest spełnialne.
* DROP UNIVERSAL QUANTIFIERS: W tym momencie wszystkie pozostałe zmienne muszą być uniwersalnie kwantyfikowane. Dlatego nie tracimy żadnych informacji, jeśli opuścimy kwantyfikator:
* ROZPOCZĘCIE V NA Λ:
Ten krok może również wymagać spłaszczenia zagnieżdżonych spójników i rozłączeń. Zdanie jest teraz w CNF i składa się z dwóch klauzul. Jest znacznie trudniejszy do odczytania niż oryginalne zdanie z implikacjami. (Może pomóc wyjaśnienie, że funkcja Skolema F(x) odnosi się do zwierzęcia potencjalnie niekochanego przez x , podczas gdy G(x) odnosi się do kogoś, kto może kochać x.) Na szczęście ludzie rzadko muszą patrzeć na zdania CNF – tłumaczenie proces jest łatwo zautomatyzowany