W naszej dyskusji na temat łączenia w przód pokazaliśmy, w jaki sposób problemy spełnienia ograniczeń (CSP) mogą być kodowane jako klauzule określone. Standardowy Prolog rozwiązuje takie problemy w dokładnie taki sam sposób, jak algorytm cofania . Ponieważ wycofywanie wylicza domeny zmiennych, działa tylko w przypadku dostawców CSP o skończonej domenie. W terminologii Prologu musi istnieć skończona liczba rozwiązań dla dowolnego celu z niezwiązanymi zmiennymi. (Na przykład problem kolorowania mapy, w którym każda zmienna może przybrać jeden z czterech różnych kolorów). CSP z nieskończoną domeną — na przykład ze zmiennymi o wartościach całkowitych lub rzeczywistych – wymagają zupełnie innych algorytmów, takich jak propagacja granic lub programowanie liniowe. Rozważmy następujący przykład. Definiujemy triangle(X,Y,Z) jako predykat, który obowiązuje, jeśli trzy argumenty są liczbami, które spełniają nierówność trójkąta:
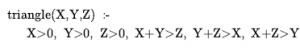
Jeśli zapytamy Prologa o trójkąt zapytań (3,4,5), to się powiedzie. Z drugiej strony, jeśli zapytamy o trójkąt(3,4,Z), nie znajdziemy rozwiązania, ponieważ podcel nie może być obsłużony przez Prolog; nie możemy porównać wartości niezwiązanej z 0. Programowanie w logice z ograniczeniami (CLP) umożliwia ograniczanie zmiennych, a nie ograniczanie. Rozwiązanie CLP to najbardziej szczegółowy zestaw ograniczeń dotyczących zmiennych zapytania, który można uzyskać z bazy wiedzy. Na przykład rozwiązaniem zapytania o trójkąt(3,4,Z) jest ograniczenie 7 > Z > 1 . Standardowe programy logiczne są tylko szczególnym przypadkiem CLP, w którym ograniczenia rozwiązania muszą być ograniczeniami równości – to znaczy powiązaniami.
Systemy CLP zawierają różne algorytmy rozwiązywania ograniczeń dla ograniczeń dozwolonych w języku. Na przykład system, który dopuszcza liniowe nierówności na zmiennych o wartościach rzeczywistych, może zawierać algorytm programowania liniowego do rozwiązywania tych ograniczeń. Systemy CLP przyjmują również znacznie bardziej elastyczne podejście do rozwiązywania standardowych zapytań programowania logicznego. Na przykład, zamiast podążania w głąb, wstecz od lewej do prawej, mogą użyć dowolnego z bardziej wydajnych algorytmów omówionych w rozdziale 6 , w tym heurystycznego porządkowania koniunkcji, backjumpingu, warunkowania zestawu cięcia i tak dalej. Systemy CLP łączą zatem elementy algorytmów spełniania ograniczeń, programowania logicznego i dedukcyjnych baz danych. Zdefiniowano kilka systemów, które pozwalają programiście na większą kontrolę nad kolejnością wyszukiwania w celu wnioskowania. Język MRS pozwala programiście na pisanie metareguł w celu określenia, które koniunkty są wypróbowywane jako pierwsze. Użytkownik może napisać regułę mówiącą, że cel z najmniejszą liczbą zmiennych powinien zostać wypróbowany jako pierwszy lub może napisać reguły specyficzne dla domeny dla poszczególnych predykatów.