Przejdziemy teraz do pięty achillesowej Prologu: rozbieżności między wyszukiwaniem w głąb i drzewem wyszukiwania, które zawierają powtarzające się stany i nieskończone ścieżki. Rozważmy następujący program logiczny, który decyduje, czy istnieje ścieżka między dwoma punktami na grafie skierowanym:

Prosty wykres trójwęzłowy, opisany przez fakty link(a,b) i link(b,c), pokazano na rysunku (a)
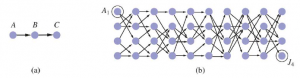
. Za pomocą tego programu ścieżka zapytania (a,c) generuje drzewo dowodowe pokazane na rysunku (a)
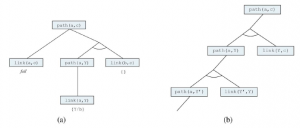
Z drugiej strony, jeśli ułożymy dwie klauzule w kolejności

następnie Prolog podąża nieskończoną ścieżką pokazaną na rysunku 9.9(b). Prolog jest zatem niekompletny jako dowodzenie twierdzeń dla klauzul określonych – nawet dla programów Datalog, jak pokazuje ten przykład – ponieważ w przypadku niektórych baz wiedzy nie dowodzi zdań, które są z nimi związane. Zauważ, że ten problem nie dotyczy łączenia w przód: po wywnioskowaniu path(a,b), path(b,c) i path(a,c) łączenie w przód zatrzymuje się. Tworzenie łańcucha wstecznego na podstawie głębokości najpierw ma również problemy z nadmiarowymi obliczeniami. Na przykład podczas znajdowania ścieżki z A1 do J4 na rysunku (b) Prolog przeprowadza 877 wnioskowania, z których większość obejmuje znalezienie wszystkich możliwych ścieżek do węzłów, z których cel jest nieosiągalny. Jest to podobne do problemu powtarzającego się stanu . Całkowita ilość wnioskowania może być wykładnicza w liczbie generowanych faktów podstawowych. Jeśli zamiast tego zastosujemy łańcuchowanie w przód, można wygenerować co najwyżej n2 path(X,Y) faktów łączących n węzłów. W przypadku problemu z rysunku (b) potrzebne są tylko 62 wnioski. Łączenie w przód w problemach wyszukiwania grafów jest przykładem programowania dynamicznego, w którym rozwiązania podproblemów są konstruowane przyrostowo z rozwiązań mniejszych podproblemów i są buforowane w celu uniknięcia ponownego przeliczenia. Podobny efekt możemy uzyskać w systemie łańcuchów wstecznych, z tą różnicą, że tutaj rozbijamy duże cele na mniejsze, zamiast je budować. Tak czy inaczej, przechowywanie wyników pośrednich w celu uniknięcia powielania jest kluczowe. Jest to podejście stosowane przez systemy programowania opartego na logice tabelarycznej, które wykorzystują wydajne mechanizmy przechowywania i wyszukiwania. Programowanie w logice tabelarycznej łączy ukierunkowanie na cel łączenia wstecz z wydajnością programowania dynamicznego w łańcuchu do przodu. Jest również kompletny dla baz wiedzy Datalog, co oznacza, że programista nie musi się martwić o nieskończone pętle. (Nadal można uzyskać nieskończoną pętlę z predykatami takimi jak ojciec(X,Y), które odnoszą się do potencjalnie nieograniczonej liczby obiektów.)