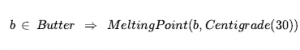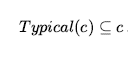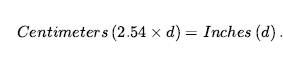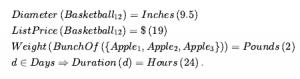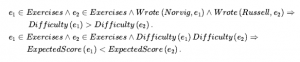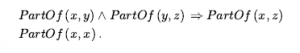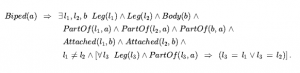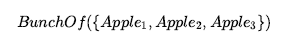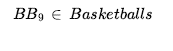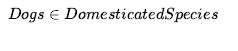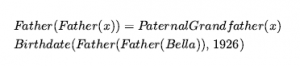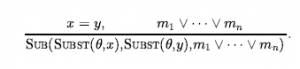Miesiąc: styczeń 2022

Omówiliśmy działania: rzeczy, które się dzieją, takie jak Shoott; i płynnie zmieniające się aspekty świata, takie jak HaveArrowt. Oba były reprezentowane jako zdania, a aksjomatami stanu następcy użyliśmy, aby powiedzieć, że biegłość będzie prawdziwa w czasie, jeśli działanie w czasie spowodowało, że było prawdziwe, lub jeśli było już prawdziwe w czasie t + 1, a działanie nie spowodować, że będzie fałszywe. To było dla świata, w którym akcje są dyskretne, natychmiastowe, zdarzają się pojedynczo i nie mają różnic w sposobie ich wykonywania (to znaczy, jest tylko jeden rodzaj akcji Strzelaj, nie ma różnicy między strzelaniem szybko, powoli nerwowo itd.). Ale gdy przechodzimy od uproszczonych dziedzin do rzeczywistego świata, istnieje znacznie bogatszy zakres działania lub zdarzenia, którymi trzeba się zająć. Rozważ działanie ciągłe, takie jak napełnianie wanny. Aksjomat stanu następcy może mówić, że wanna jest pusta przed akcją i pełna po zakończeniu akcji, ale nie może mówić o tym, co dzieje się podczas akcji. Nie jest też w stanie opisać dwóch czynności dziejących się w tym samym czasie – takich jak mycie zębów podczas oczekiwania na wypełnienie wanny. Aby poradzić sobie z takimi przypadkami, wprowadzamy podejście znane jako rachunek zdarzeń. Obiektami rachunku zdarzeń są zdarzenia, biegły i punkty czasowe. At(Shankar,Berkeley) jest płynny: przedmiot, który odnosi się do faktu przebywania Shankara w Berkeley. Wydarzenie E₁ Shankara lecącego z San Francisco do Waszyngtonu jest opisane jako

gdzie Flyings to kategoria wszystkich zawodów lotniczych. Reifikując zdarzenia umożliwiamy dodanie dowolnej ilości dowolnych informacji o nich. Na przykład możemy powiedzieć, że lot Shankara był wyboisty z Bumpy(E₁). W ontologii, w której zdarzenia są n-arnymi predykatami, nie byłoby możliwości dodania takich dodatkowych informacji; przejście do predykatu n+1 nie jest rozwiązaniem skalowalnym. Aby stwierdzić, że biegły jest rzeczywiście prawdziwy, zaczynając od pewnego momentu t1 i kontynuując do czasu t₂ , używamy predykatu T , tak jak w T(At(Shankar, Berkeley) t₁,t₂) . Podobnie używamy Happens(E₁,t₁,t₂), aby powiedzieć, że zdarzenie E₁ rzeczywiście miało miejsce, zaczynając w czasie t₁ i kończąc w czasie t₂ . Kompletny zestaw predykatów dla jednej wersji rachunku zdarzeń to:

T (f, t1, t2) : Płynne f jest prawdziwe dla wszystkich czasów między t1 a t2

Dzieje się (e, t1, t2) : Zdarzenie e rozpoczyna się o godzinie t1 i kończy o godzinie t2

Inicjuje (e, f, t): Zdarzenie e powoduje, że płynne f staje się prawdziwe w czasie t

Kończy (e, f, t): Zdarzenie e powoduje, że płynne f przestaje być prawdziwe w czasie t

Zainicjowane (f, t1, t2) : Płynne f staje się prawdziwe w pewnym momencie między t1 i t2

Zakończony (f, t1, t2) : Płynne f przestaje być prawdziwe w pewnym momencie między t1 i t2

t1 < t2 : Punkt czasowy t1 występuje przed czasem t2

Skutki zdarzenia lotniczego możemy opisać:

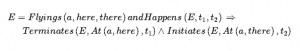
Zakładamy wyróżnione zdarzenie Start, które opisuje stan początkowy, mówiąc, które biegły są prawdziwe (przy użyciu Initiates) lub fałszywe (przy użyciu Terminated) w momencie rozpoczęcia. Możemy wtedy opisać, które biegły są prawd ziwe w jakich momentach za pomocą pary aksjomatów dla T i że ¬T postępuj zgodnie z tym samym ogólnym formatem, co aksjomaty stanu następcy: Załóżmy, że zdarzenie ma miejsce między czasem t1 i t3 , a w t2 gdzieś w tym przedziale czasu zdarzenie zmienia wartość płynnego f , albo inicjując je (uczyniając je prawdziwym) albo kończąc ( czyniąc to fałszywym). Następnie w czasie t4 w przyszłości, jeśli żadne inne zdarzenie nie zmieniło biegłości (odpowiednio albo ją przerwało, albo zainicjowało), to biegły zachowa swoją wartość. Formalnie aksjomaty to:

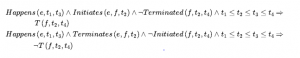
gdzie Zakończone i Zainicjowane są zdefiniowane przez:

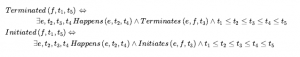
Możemy rozszerzyć rachunek zdarzeń, aby reprezentować zdarzenia jednoczesne (takie jak dwie osoby niezbędne do jazdy na huśtawce), zdarzenia egzogeniczne (takie jak wiatr poruszający obiektem), zdarzenia ciągłe (takie jak przypływ pływu), zdarzenia niedeterministyczne (takie jak jak rzucanie monetą i wyrzucanie resztek lub reszek) i inne komplikacje.

Świat rzeczywisty można postrzegać jako składający się z podstawwoych obiektów (np. cząstek atomowych) i zbudowanych z nich obiektów złożonych. Rozumując na poziomie dużych obiektów, takich jak jabłka i samochody, możemy przezwyciężyć złożoność związaną z indywidualnym radzeniem z ogromną liczbą prymitywnych obiektów. Istnieje jednak znaczna część rzeczywistości, która zdaje się przeczyć jakiejkolwiek oczywistej indywidualizacji – podziałowi na odrębne obiekty. Nadajemy tej części ogólną nazwę. Załóżmy na przykład, że mam przed sobą masło i mrównik. Mogę powiedzieć, że jest jeden mrównik, ale nie ma oczywistej liczby „obiektów maślanych”, ponieważ każda część obiektu masła jest również obiektem masła, przynajmniej dopóki rzeczywiście nie dojdziemy do bardzo małych części. To jest główna różnica między rzeczami a rzeczami. Jeśli przetniemy mrównik na pół, nie otrzymamy dwóch mrówników (niestety). Język angielski wyraźnie rozróżnia rzeczy i rzeczy. Mówimy „aardvark”, ale poza pretensjonalnymi kalifornijskimi restauracjami nie można powiedzieć „masło”. Językoznawcy rozróżniają rzeczowniki liczące, takie jak mrówniki, dziury i twierdzenia, oraz rzeczowniki masowe, takie jak masło, woda i energia. Kilka konkurencyjnych ontologii twierdzi, że radzi sobie z tym rozróżnieniem. Tutaj opisujemy tylko jeden; pozostałe omówiono w dziale notatek historycznych. Aby właściwie przedstawić rzeczy, zaczynamy od tego, co oczywiste. Musimy mieć jako obiekty w naszej ontologii przynajmniej grube „bryły” rzeczy, z którymi wchodzimy w interakcję. Na przykład możemy rozpoznać bryłkę masła jako tę, która została na stole poprzedniego wieczoru; możemy to odebrać, zważyć, sprzedać lub cokolwiek innego. W tym sensie jest to przedmiot podobny do mrównika. Nazwijmy to Butter₃. Definiujemy również kategorię Masło. Nieformalnie jej elementami będą wszystkie te rzeczy, o których można by powiedzieć „To masło”, w tym Butter₃. Z pewnymi zastrzeżeniami dotyczącymi bardzo małych części, które na razie pominiemy, każda część obiektu masła jest również obiektem butter

Możemy teraz powiedzieć, że masło topi się w temperaturze około 30 stopni Celsjusza:

Można powiedzieć, że masło jest żółte, ma mniejszą gęstość niż woda, jest miękkie w temperaturze pokojowej, ma wysoką zawartość tłuszczu i tak dalej. Z drugiej strony masło nie ma określonego rozmiaru, kształtu ani wagi. Możemy zdefiniować bardziej wyspecjalizowane kategorie masła, takie jak masło niesolone, które też jest rodzajem rzeczy. Zauważ, że kategoria PoundOfButter, która obejmuje jako członków wszystkie masło-obiekty ważące jeden funt, nie jest rodzajem rzeczy. Jeśli przetniemy funt masła na pół, niestety nie dostaniemy dwóch funtów masła. W rzeczywistości dzieje się tak: niektóre właściwości są nieodłączne: należą do samej substancji przedmiotu, a nie do przedmiotu jako całości. Kiedy przetniesz egzemplarz czegoś na pół, dwa kawałki zachowują wewnętrzne właściwości — takie jak gęstość, temperatura wrzenia, smak, kolor, własność i tak dalej. Z drugiej strony ich zewnętrzne właściwości — waga, długość, kształt itd. — nie są zachowywane w ramach podziału. Kategoria przedmiotów, która zawiera w swojej definicji tylko wewnętrzne właściwości, jest więc substancją, czyli rzeczownikiem masowym; klasa, która zawiera w swojej definicji wszelkie zewnętrzne właściwości, jest rzeczownikiem licznika. Rzeczy i Rzecz to, odpowiednio, najbardziej ogólne kategorie substancji i przedmiotów.

Zarówno w naukowych, jak i zdroworozsądkowych teoriach świata przedmioty mają wysokość, masę, koszt i tak dalej. Wartości, które przypisujemy tym właściwościom, nazywamy miarami. Zwykłe miary ilościowe są dość łatwe do przedstawienia. Wyobrażamy sobie, że wszechświat zawiera abstrakcyjne „obiekty pomiarowe”, takie jak długość, która jest długością tego odcinka linii:|—————————-| . Możemy nazwać tę długość 1,5 cala lub 3,81 centymetra. Tak więc ta sama długość ma różne nazwy w naszym języku. Reprezentujemy długość za pomocą funkcji jednostek, która jako argument przyjmuje liczbę.

Naturalne rodzaje

Niektóre kategorie mają ścisłe definicje: obiekt jest trójkątem wtedy i tylko wtedy, gdy jest wielokątem o trzech bokach. Z drugiej strony większość kategorii w świecie rzeczywistym nie ma jednoznacznej definicji; są to tak zwane kategorie rodzaju naturalnego. Na przykład pomidory wydają się być matowe, szkarłatne; z grubsza kulisty; z wcięciem u góry w miejscu łodygi; około dwóch do czterech cali średnicy; o cienkiej, ale twardej skórze; oraz z miąższem, nasionami i sokiem w środku. Istnieje jednak zróżnicowanie: niektóre pomidory są żółte lub pomarańczowe, niedojrzałe pomidory są zielone, niektóre są mniejsze lub większe niż przeciętne, a pomidorki koktajlowe są jednakowo małe. Zamiast mieć pełną definicję pomidorów, mamy zestaw funkcji, które służą do identyfikacji obiektów, które są wyraźnie typowymi pomidorami, ale mogą nie identyfikować ostatecznie innych obiektów. (Czy może istnieć pomidor, który jest puszysty jak brzoskwinia?) Stanowi to problem dla agenta logicznego. Agent nie może być pewien, że postrzegany przez niego przedmiot jest pomidorem, a nawet gdyby był pewien, nie mógłby być pewien, jakie właściwości ma ten typowy pomidor. Ten problem jest nieuniknioną konsekwencją działania w częściowo obserwowalnych środowiskach. Jednym z przydatnych podejść jest oddzielenie tego, co jest prawdziwe we wszystkich przypadkach kategorii, od tego, co jest prawdziwe tylko w przypadku typowych przypadków. Tak więc oprócz kategorii Pomidory będziemy mieli również kategorię Typowe (Pomidory). Tutaj funkcja Typowa odwzorowuje kategorię na podklasę, która zawiera tylko typowe instancje:

Większość wiedzy o naturalnych gatunkach dotyczy ich typowych przypadków:

W ten sposób możemy zapisywać przydatne fakty dotyczące kategorii bez dokładnych definicji. Trudność w dostarczeniu dokładnych definicji dla większości kategorii naturalnych została dogłębnie wyjaśniona przez Wittgensteina (1953). Posłużył się przykładem gier, aby pokazać, że członkowie kategorii mają wspólne „podobieństwa rodzinne”, a nie konieczne i wystarczające cechy: jaka ścisła definicja obejmuje szachy, berka, pasjansa i zbijaka? Użyteczność pojęcia ścisłej definicji zakwestionował także Quine. Wskazał, że nawet definicja „kawalera” jako niezamężnego dorosłego mężczyzny jest podejrzana; można na przykład zakwestionować stwierdzenie w rodzaju „Papież jest kawalerem”. Chociaż nie jest to całkowicie fałszywe, to użycie jest z pewnością niefortunne, ponieważ wywołuje niezamierzone wnioski ze strony słuchacza. Napięcie można by chyba rozwiązać, rozróżniając definicje logiczne odpowiednie do wewnętrznej reprezentacji wiedzy od bardziej zniuansowanych kryteriów szczęśliwego użycia językowego. To ostatnie można osiągnąć poprzez „filtrowanie” twierdzeń wywodzących się z tego pierwszego. Możliwe jest również, że błędy w użyciu językowym służą jako informacja zwrotna do modyfikacji wewnętrznych definicji, tak że filtrowanie staje się niepotrzebne. Jeśli odcinek linii nazywa się L₁, możemy napisać

Konwersja między jednostkami odbywa się poprzez porównanie wielokrotności jednej jednostki do drugiej:

Podobne aksjomaty można zapisać dla funtów i kilogramów, sekund i dni oraz dolarów i centów. Miary mogą być używane do opisu obiektów w następujący sposób:

Zauważ, że $(1) nie jest dolarem — to cena. Można mieć dwa banknoty dolarowe, ale istnieje tylko jeden obiekt o nazwie $(1) . Zauważ również, że chociaż cale(0) i centymetry(0) odnoszą się do tej samej zerowej długości, nie są one identyczne z innymi zerowymi miarami, takimi jak sekundy(0). Proste, ilościowe miary są łatwe do przedstawienia. Inne miary stanowią większy problem, ponieważ nie mają uzgodnionej skali wartości. Ćwiczenia mają trudności, desery mają smakowitość, a wiersze piękno, ale tym walorom nie można przypisać liczb. Można by w chwili czystej księgowości odrzucić takie właściwości jako bezużyteczne dla celów logicznego rozumowania; lub, co gorsza, próbować narzucić pięknu skalę liczbową. Byłby to poważny błąd, ponieważ jest niepotrzebny. Najważniejszym aspektem miar nie są poszczególne wartości liczbowe, ale możliwość uporządkowania miar. Chociaż miary nie są liczbami, nadal możemy je porównywać, używając symbolu porządkowania, takiego jak . Na przykład możemy uwierzyć, że ćwiczenia Norviga są trudniejsze niż ćwiczenia Russella i że trudniejsze ćwiczenia mają mniej punktów:

To wystarczy, aby zdecydować, które ćwiczenia wykonać, mimo że nigdy nie używano wartości liczbowych trudności. (Trzeba jednak odkryć, kto napisał które ćwiczenia). Tego rodzaju monotoniczne relacje między miarami stanowią podstawę dziedziny fizyki jakościowej, poddziedziny sztucznej inteligencji, która bada, jak wnioskować o układach fizycznych bez zagłębiania się w szczegółowe równania i symulacje numeryczne. Fizyka jakościowa jest omówiona w dziale notatek historycznych.

Pomysł, że jeden obiekt może być częścią innego, jest znany. Czyjś nos jest częścią czyjejś głowy, Rumunia jest częścią Europy, a ten rozdział jest częścią tej książki. Używamy ogólnej relacji PartOf, aby powiedzieć, że jedna rzecz jest częścią innej. Obiekty można grupować w hierarchie PartOf, przypominające hierarchię Podzbioru:

Część relacji jest przechodnia i zwrotna; to jest,

Dlatego możemy zawrzeć PartOf (Bukareszt, Ziemia). Kategorie obiektów złożonych często charakteryzują się strukturalnymi powiązaniami między częściami. Na przykład dwunożny to obiekt, który ma dokładnie dwie nogi przymocowane do ciała:

Notacja „dokładnie dwa” jest trochę niezręczna; jesteśmy zmuszeni powiedzieć, że istnieją dwie nogi, że nie są takie same i że jeśli ktoś proponuje trzecią, to musi być taka sama jak jedna z dwóch pozostałych.

Możemy zdefiniować relację PartPartition analogiczną do relacji Partition dla kategorii. Obiekt składa się z części w jego PartPartition i może być postrzegany jako pochodzący z niektórych właściwości z tych części. Na przykład masa obiektu złożonego jest sumą mas części. Zauważ, że tak nie jest w przypadku kategorii, które nie mają masy, nawet jeśli ich elementy mogą.

Przydatne jest również zdefiniowanie obiektów złożonych z określonymi częściami, ale bez określonej struktury. Na przykład możemy chcieć powiedzieć „Jabłka w tej torbie ważą dwa funty”. Pokusą byłoby przypisanie tej wagi do zbioru jabłek w torbie, ale byłoby to błędem, ponieważ zbiór jest abstrakcyjnym pojęciem matematycznym, które ma elementy, ale nie ma wagi. Zamiast tego potrzebujemy nowej koncepcji, którą nazwiemy wiązką. Na przykład, jeśli jabłka to Apple₁, Appple₂ i Apple₃, to

oznacza obiekt złożony z trzema jabłkami jako częściami (nie elementami). Możemy wtedy użyć wiązki jako normalnego, aczkolwiek nieustrukturyzowanego obiektu. Zauważ, że BunchOf({x}) = x . Ponadto BunchOf (jabłka) to złożony obiekt składający się ze wszystkich jabłek — nie należy mylić z jabłkami, kategorią lub zbiorem wszystkich jabłek. Możemy zdefiniować BunchOf w kategoriach relacji PartOf. Oczywiście każdy element jest częścią BunchOf (s):

Ponadto BunchOf (s) to najmniejszy obiekt spełniający ten warunek. Innymi słowy, BunchOf (s) musi być częścią dowolnego obiektu, który ma wszystkie elementy jako części:

Aksjomaty te są przykładem ogólnej techniki zwanej minimalizacją logiczną, która oznacza zdefiniowanie obiektu jako najmniejszego spełniającego określone warunki.

Organizacja obiektów w kategorie jest istotną częścią reprezentacji wiedzy. Chociaż interakcja ze światem odbywa się na poziomie pojedynczych obiektów, wiele rozumowań odbywa się na poziomie kategorii. Na przykład kupujący zwykle miałby na celu zakup piłki do koszykówki, a nie konkretnej piłki do koszykówki, takiej jak BB₉ . Kategorie służą również do przewidywania obiektów po ich sklasyfikowaniu. Wnioskuje się obecność pewnych obiektów z danych wejściowych percepcyjnych, wnioskuje przynależność do kategorii na podstawie postrzeganych właściwości obiektów, a następnie wykorzystuje informacje o kategorii do przewidywania obiektów. Na przykład z zielonej i żółtej nakrapianej skóry, średnicy jednej stopy, jajowatego kształtu, czerwonego miąższu, czarnych nasion i obecności w alejce z owocami można wywnioskować, że przedmiot jest arbuzem; z tego wnioskuje się, że przydałby się do sałatek owocowych.

Istnieją dwie możliwości reprezentowania kategorii w logice pierwszego rzędu: predykaty i obiekty. Oznacza to, że możemy użyć predykatu Basketball(b) lub możemy zreifikować kategorię jako obiekt, Basketballs. Moglibyśmy wtedy powiedzieć Member(b,Basketballs), który będziemy skracać do b  Basketalls, można powiedzieć, że b należy do kategorii piłek do koszykówki. Mówimy Subset(Basketballs,balls), w skrócie Basketballs  Balls , aby powiedzieć, że Basketballs jest podkategorią Piłki. Podkategorii, podklasy i podzbioru będziemy używać zamiennie.

Kategorie porządkują wiedzę poprzez dziedziczenie. Jeśli powiemy, że wszystkie wystąpienia kategorii Żywność są jadalne i jeśli stwierdzimy, że Owoc jest podklasą Żywności, a Jabłka jest podklasą Owoców, możemy wywnioskować, że każde jabłko jest jadalne. Mówimy, że poszczególne jabłka dziedziczą właściwość jadalności, w tym przypadku z ich przynależności do kategorii Żywność. Relacje podklas organizują kategorie w hierarchię taksonomiczną lub taksonomię. Taksonomie były używane od wieków w dziedzinach technicznych. Największa taka taksonomia porządkuje około 10 milionów żyjących i wymarłych gatunków, z których wiele to chrząszcze, w jedną hierarchię; bibliotekoznawstwo opracowało taksonomię wszystkich dziedzin wiedzy, zakodowaną jako system dziesiętny Deweya; a organy podatkowe i inne departamenty rządowe opracowały obszerne taksonomie zawodów i produktów handlowych.

Logika pierwszego rzędu ułatwia określanie faktów na temat kategorii, czy to przez powiązanie obiektów z kategoriami, czy przez kwantyfikację ich elementów. Oto kilka przykładowych faktów:

* Obiekt jest członkiem kategorii.

* Kategoria jest podklasą innej kategorii.

* Wszyscy członkowie kategorii mają pewne właściwości.

* Członkowie kategorii mogą być rozpoznawani przez niektóre właściwości.

* Kategoria jako całość ma pewne właściwości.

Zauważ, że ponieważ Pies jest kategorią i należy do Gatunków Udomowionych, ten ostatni musi być kategorią kategorii. Oczywiście są wyjątki od wielu z powyższych zasad (przebite piłki do koszykówki nie są sferyczne); tymi wyjątkami zajmiemy się później. Chociaż relacje podklas i składowych są najważniejsze dla kategorii, chcemy również móc określić relacje między kategoriami, które nie są podklasami względem siebie. Na przykład, jeśli po prostu powiemy, że studenci i studenci są podklasami Studentów, to nie powiedzieliśmy, że licencjat nie może być również studentem studiów magisterskich. Mówimy, że dwie lub więcej kategorii jest rozłącznych, jeśli nie mają wspólnych członków. Można też powiedzieć, że zajęcia licencjackie i magisterskie tworzą wyczerpujący rozkład studentów. Wyczerpujący rozkład zbiorów rozłącznych jest znany jako partycja. Oto kilka przykładów tych trzech koncepcji:

(Zauważ, że Wyczerpująca Dekompozycja Amerykanów Północnych nie jest podziałem, ponieważ niektórzy ludzie mają podwójne obywatelstwo.) Trzy predykaty są zdefiniowane w następujący sposób:

Kategorie mogą być również definiowane poprzez zapewnienie niezbędnych i wystarczających warunków członkostwa. Na przykład kawaler to nieżonaty dorosły mężczyzna:

Ścisłe logiczne definicje kategorii są zwykle możliwe tylko dla sztucznych terminów formalnych, a nie dla zwykłych obiektów. Ale definicje nie zawsze są potrzebne.

W domenach „zabawkowych” wybór reprezentacji nie jest tak ważny; wiele opcji będzie działać. Złożone domeny, takie jak zakupy w Internecie czy jazda samochodem w ruchu, wymagają bardziej ogólnych i elastycznych reprezentacji. Ten rozdział pokazuje, jak tworzyć te reprezentacje, koncentrując się na ogólnych pojęciach — takich jak zdarzenia, czas, obiekty fizyczne i przekonania — które występują w wielu różnych dziedzinach. Reprezentowanie tych abstrakcyjnych pojęć jest czasami nazywane inżynierią ontologiczną. Nie możemy mieć nadziei, że przedstawimy wszystko na świecie, nawet 1000-stronicowy podręcznik, ale zostawimy miejsca, w których zmieści się nowa wiedza dla dowolnej domeny. Na przykład określimy, co to znaczy być fizycznym obiektem, a szczegóły różnych typów obiektów — robotów, telewizorów, książek lub czegokolwiek — można później wypełnić. Jest to analogiczne do sposobu, w jaki projektanci struktur programistycznych zorientowanych obiektowo (takich jak środowisko graficzne Java Swing) definiują ogólne koncepcje, takie jak Window, oczekując, że użytkownicy będą używać ich do definiowania bardziej szczegółowych pojęć, takich jak SpreadsheetWindow. Ogólna struktura pojęć nazywana jest wyższą ontologią ze względu na konwencję rysowania grafów z pojęciami ogólnymi na górze i pojęciami bardziej szczegółowymi pod nimi, jak na rysunku

Zanim dalej zajmiemy się ontologią, powinniśmy podać jedno ważne zastrzeżenie. Zdecydowaliśmy się użyć logiki pierwszego rzędu do omawiania zawartości i organizacji wiedzy, chociaż niektóre aspekty realnego świata są trudne do uchwycenia w FOL. Główna trudność polega na tym, że większość uogólnień ma wyjątki lub obowiązuje tylko do pewnego stopnia. Na przykład, chociaż „pomidory są czerwone” jest użyteczną zasadą, niektóre pomidory są zielone, żółte lub pomarańczowe. Podobne wyjątki można znaleźć w prawie wszystkich regułach w tym rozdziale. Umiejętność radzenia sobie z wyjątkami i niepewnością jest niezwykle ważna, ale jest ortogonalna do zadania polegającego na zrozumieniu ogólnej ontologii. Jaki jest pożytek z wyższej ontologii? Rozważ ontologię obwodów. Zawiera wiele upraszczających założeń: całkowicie pomija się czas; sygnały są stałe i nie rozchodzą się; struktura obwodu pozostaje stała. Bardziej ogólna ontologia uwzględniałaby sygnały w określonych momentach i obejmowałaby długości przewodów i opóźnienia propagacji. To pozwoliłoby nam symulować właściwości czasowe obwodu i rzeczywiście takie symulacje są często przeprowadzane przez projektantów obwodów. Moglibyśmy również wprowadzić ciekawsze klasy bramek, na przykład opisując technologię (TTL, CMOS itd.) oraz specyfikację wejścia-wyjścia. Gdybyśmy chcieli omówić niezawodność lub diagnozę, uwzględnilibyśmy możliwość spontanicznej zmiany struktury obwodu lub właściwości bramek. Aby uwzględnić rozproszenie pojemności, musielibyśmy przedstawić, gdzie znajdują się przewody na płytce. Jeśli spojrzymy na świat wumpusów, mamy do czynienia z podobnymi rozważaniami. Chociaż reprezentujemy czas, ma on prostą strukturę: nic się nie dzieje poza momentami działania agenta, a wszystkie zmiany są natychmiastowe. Bardziej ogólna ontologia, lepiej dopasowana do świata rzeczywistego, pozwoliłaby na jednoczesne zmiany rozciągnięte w czasie. Użyliśmy również predykatu zagłębienia, aby powiedzieć, które kwadraty mają zagłębienia. Mogliśmy pozwolić na różne rodzaje dołów, mając kilka osobników należących do klasy dołów, z których każdy ma inne właściwości. Podobnie możemy chcieć pozwolić na inne zwierzęta oprócz wumpusów. Być może nie da się określić dokładnego gatunku na podstawie dostępnych spostrzeżeń, więc musielibyśmy stworzyć biologiczną taksonomię, aby pomóc agentowi przewidzieć zachowanie mieszkańców jaskini na podstawie skąpych wskazówek. W przypadku każdej ontologii specjalnego przeznaczenia możliwe jest dokonanie takich zmian, aby przejść w kierunku większej ogólności. Powstaje wtedy oczywiste pytanie: czy wszystkie te ontologie zbiegają się w ontologii ogólnego przeznaczenia? Po wiekach filozoficznych i obliczeniowych dociekań odpowiedź brzmi „może”. W tej części przedstawiamy jedną ontologię ogólnego przeznaczenia, która łączy idee z tamtych wieków. Dwie główne cechy ontologii ogólnego przeznaczenia odróżniają je od zbiorów ontologii specjalnego przeznaczenia:

* Ontologia ogólnego przeznaczenia powinna mieć zastosowanie w mniej więcej dowolnej domenie specjalnego przeznaczenia (z dodatkiem aksjomatów dziedzinowych). Oznacza to, że żaden problem reprezentacyjny nie może być finezyjny ani zamiatany pod dywan.

* W każdej wystarczająco wymagającej dziedzinie różne obszary wiedzy muszą być ujednolicone, ponieważ rozumowanie i rozwiązywanie problemów może obejmować kilka obszarów jednocześnie. Na przykład system naprawy obwodów robota musi analizować obwody pod kątem połączeń elektrycznych i układu fizycznego oraz czasu, zarówno w celu analizy synchronizacji obwodów, jak i szacowania pracy, którą można połączyć z tymi, które opisują układ przestrzenny i muszą działać równie dobrze dla nanosekund i minut oraz dla angstremów i metrów.

Powinniśmy z góry powiedzieć, że przedsięwzięcie ogólnej inżynierii ontologicznej odniosło jak dotąd jedynie ograniczony sukces. Żadna z najlepszych aplikacji AI  nie korzysta z ogólnej ontologii – wszystkie wykorzystują inżynierię wiedzy specjalnego przeznaczenia i maszynę uczenia się. Względy społeczne/polityczne mogą utrudnić konkurującym stronom uzgodnienie ontologii. Jak mówi Tom Gruber : „Każda ontologia jest traktatem – umową społeczną – pomiędzy ludźmi, dla których istnieje jakiś wspólny motyw dzielenia się”. Kiedy rywalizujące obawy przeważają nad motywacją do dzielenia się, nie może być wspólnej ontologii. Im mniejsza liczba interesariuszy, tym łatwiej jest stworzyć ontologię, a co za tym idzie trudniej stworzyć ontologię ogólnego przeznaczenia niż taką o ograniczonym przeznaczeniu, taką jak Open Biomedical Ontology (Smith i in., 2007). Te ontologie, które istnieją, zostały stworzone czterema ścieżkami:

1. Przez zespół przeszkolonych ontologów lub logików, którzy projektują ontologię i piszą aksjomaty. System CYC był w większości zbudowany w ten sposób.
2. Importując kategorie, atrybuty i wartości z istniejącej bazy danych lub baz danych. DBPEDIA została zbudowana poprzez import ustrukturyzowanych faktów z Wikipedii.
3. Analizując dokumenty tekstowe i wydobywając z nich informacje. TEXTRUNNER został zbudowany poprzez czytanie dużego zbioru stron internetowych.
4. Zachęcając niewykwalifikowanych amatorów do wchodzenia w wiedzę zdroworozsądkową. System OPENMIND został zbudowany przez wolontariuszy, którzy przedstawiali fakty w języku angielskim.

Na przykład w Grafie wiedzy Google wykorzystano częściowo ustrukturyzowaną treść z Wikipedii, łącząc ją z innymi treściami zebranymi z całej sieci pod nadzorem człowieka. Zawiera ponad 70 miliardów faktów i dostarcza odpowiedzi na około jedną trzecią wyszukiwań w Google

Wcześniej pokazano, w jaki sposób agent z bazą wiedzy może wyciągać wnioski, które umożliwiają mu właściwe działanie. Tu odpowiadamy na pytanie, jakie treści umieścić w bazie wiedzy takiego agenta – jak reprezentować fakty dotyczące świata. Będziemy używać logiki pierwszego rzędu jako języka reprezentacji, ale w kolejnych częściach wprowadzimy różne formalizmy reprezentacji, takie jak hierarchiczne sieci zadań do wnioskowania o planach, sieci bayesowskie do wnioskowania z niepewnością , modele Markowa do wnioskowania o czas oraz głębokie sieci neuronowe do wnioskowania o obrazach, dźwiękach i innych danych. Ale bez względu na to, jakiego przedstawienia użyjesz, fakty dotyczące świata nadal wymagają rozwiązania, a ten rozdział daje ci wyczucie problemów

Pokazaliśmy, w jaki sposób logika pierwszego rzędu może reprezentować prosty scenariusz ze świata rzeczywistego, obejmujący takie pojęcia, jak sprzedaż, broń i obywatelstwo. Ale złożone scenariusze rzeczywistego świata mają zbyt wiele niepewności i zbyt wiele niewiadomych. Logika okazała się bardziej skuteczna w scenariuszach obejmujących formalne, ściśle określone koncepcje, takie jak synteza i weryfikacja zarówno sprzętu, jak i oprogramowania. Badania dowodzące twierdzeń są prowadzone w dziedzinie projektowania sprzętu, języków programowania i inżynierii oprogramowania – nie tylko w sztucznej inteligencji. W przypadku sprzętu aksjomaty opisują interakcje między sygnałami a elementami obwodu. Logiczne wnioskowania zaprojektowane specjalnie do weryfikacji były w stanie zweryfikować całe procesory, w tym ich właściwości czasowe. Dowód twierdzenia AURA został zastosowany do projektowania obwodów, które są bardziej zwarte niż jakikolwiek inny projekt . W przypadku oprogramowania wnioskowanie o programach jest dość podobne do wnioskowania o akcjach: aksjomaty opisują warunki wstępne i skutki każdej instrukcji. Formalna synteza algorytmów była jednym z pierwszych zastosowań dowodzenia twierdzeń, jak nakreślił to Cordell Green , który oparł się na wcześniejszych pomysłach Herberta Simona . Chodzi o to, aby konstruktywnie udowodnić twierdzenie, że „istnieje program spełniający określoną specyfikację”. Chociaż w pełni zautomatyzowana synteza dedukcyjna, jak się ją nazywa, nie stała się jeszcze możliwa do zastosowania w programowaniu ogólnego przeznaczenia, ręcznie sterowana synteza dedukcyjna odniosła sukces w projektowaniu kilku nowatorskich i zaawansowanych algorytmów. Aktywnym obszarem badań jest również synteza programów celowych, takich jak naukowy kod obliczeniowy. Podobne techniki są obecnie stosowane do weryfikacji oprogramowania przez systemy takie jak kontroler modeli SPIN . Na przykład program kontroli statku kosmicznego Remote Agent został zweryfikowany przed lotem i po nim .Klucz publiczny RSA, algorytm szyfrowania i algorytm dopasowywania ciągów Boyer-Moore zostały zweryfikowane w ten sposób .

Streszczenie

Przedstawiliśmy analizę wnioskowania logicznego w logice pierwszego rzędu oraz szereg algorytmów do tego.

* Pierwsze podejście wykorzystuje reguły wnioskowania (instancja uniwersalna i egzystencjalna) w celu przedstawienia problemu wnioskowania. Zazwyczaj to podejście jest powolne, chyba że domena jest mała.

* Użycie unifikacji do identyfikacji odpowiednich podstawień dla zmiennych eliminuje etap tworzenia instancji w dowodach pierwszego rzędu, czyniąc proces bardziej wydajnym w wielu przypadkach.

* Podniesiona wersja Modus Ponens wykorzystuje unifikację, aby zapewnić naturalną i potężną regułę wnioskowania, uogólnioną Modus Ponens. Algorytmy tworzenia łańcuchów w przód i w tył stosują tę zasadę do zestawów klauzul określonych.

* Uogólniony Modus Ponens jest kompletny dla zdań określonych, chociaż problem implikacji jest częściowo rozstrzygalny. W przypadku baz wiedzy Datalog składających się z niefunkcjonalnych klauzul określonych, rozstrzygnięcie jest możliwe.

* Łańcuchy do przodu są używane w dedukcyjnych bazach danych, gdzie można je łączyć z operacjami na relacyjnych bazach danych. Jest również używany w systemach produkcyjnych, które wykonują wydajne aktualizacje z bardzo dużymi zestawami reguł. Tworzenie łańcucha w przód jest zakończone dla Datalog i działa w czasie wielomianowym.

* Łańcuchy wsteczne są używane w systemach programowania logicznego, które wykorzystują zaawansowaną technologię kompilatora, aby zapewnić bardzo szybkie wnioskowanie. Łańcuchy wsteczne cierpią z powodu nadmiarowych wnioskowań i nieskończonych pętli; można je złagodzić poprzez zapamiętywanie.

* Prolog, w przeciwieństwie do logiki pierwszego rzędu, używa zamkniętego świata z założeniem unikalnych nazw i negacją jako porażką. Dzięki temu Prolog jest bardziej praktycznym językiem programowania, ale oddala go od czystej logiki.

* Uogólniona reguła wnioskowania o rozdzielczości zapewnia kompletny system dowodowy dla logiki pierwszego rzędu, wykorzystujący bazy wiedzy w spójnej postaci normalnej.

* Istnieje kilka strategii zmniejszania przestrzeni wyszukiwania w systemie rozdzielczości bez narażania kompletności. Jedną z najważniejszych kwestii jest zajmowanie się równością; pokazaliśmy, jak można zastosować demodulację i paramodulację.

* Wydajne dowodzenie twierdzeń oparte na rozdzielczości zostało użyte do udowodnienia interesujących twierdzeń matematycznych oraz do weryfikacji i syntezy oprogramowania i sprzętu.

Wiemy, że wielokrotne stosowanie reguły wnioskowania rozdzielczości ostatecznie znajdzie dowód, jeśli taki istnieje. W tym podrozdziale przyjrzymy się strategiom, które pomagają skutecznie znajdować dowody.

PREFERENCJA JEDNOSTEK: Ta strategia preferuje rozwiązania, w których jedno ze zdań jest pojedynczym literałem (znanym również jako klauzula jednostkowa). Ideą strategii jest to, że próbujemy stworzyć pustą klauzulę, więc dobrym pomysłem może być preferowanie wnioskowania, które tworzą krótsze zdania. Rozwiązanie zdania jednostkowego (takiego jak P ) z dowolnym innym zdaniem (takim jak ¬P V ¬Q V R ) zawsze daje klauzulę (w tym przypadku ¬Q V R ), która jest krótsza niż druga klauzula. Kiedy strategia preferencji jednostkowych została po raz pierwszy wypróbowana dla wnioskowania zdaniowego w 1964 r., doprowadziła ona do dramatycznego przyspieszenia, umożliwiając udowodnienie twierdzeń, z którymi nie można sobie poradzić bez preferencji. Rozdzielczość jednostkowa to ograniczona forma rozwiązywania, w której każdy krok rozstrzygania musi zawierać klauzulę jednostkową. Rozstrzyganie jednostek jest ogólnie niekompletne, ale kompletne w przypadku klauzul Horn. Dowody rozdzielczości jednostek w klauzulach Horn przypominają łańcuchowanie w przód.

Dowód twierdzenia OTTER , wykorzystuje formę przeszukiwania najlepszy-pierwszy. Jego funkcja heurystyczna mierzy „wagę” każdej klauzuli, przy czym preferowane są klauzule lżejsze. Dokładny wybór heurystyki zależy od użytkownika, ale generalnie waga klauzuli powinna być skorelowana z jej rozmiarem lub trudnością. Klauzule jednostkowe są traktowane jako lekkie; poszukiwania można zatem postrzegać jako uogólnienie strategii preferencji jednostkowych.

ZESTAW WSPARCIA: Preferencje, które najpierw wypróbowują określone rozdzielczości, są pomocne, ale ogólnie lepiej jest spróbować całkowicie wyeliminować niektóre potencjalne rozwiązania. Na przykład możemy nalegać, aby każdy krok rozwiązywania zawierał co najmniej jeden element specjalnego zestawu klauzul – zestawu wsparcia. Rezolwenta jest następnie dodawana do zestawu podpór. Jeśli zestaw wsparcia jest mały w stosunku do całej bazy wiedzy, przestrzeń poszukiwań zostanie drastycznie zmniejszona.

Aby zapewnić kompletność tej strategii, możemy dobrać zbiór podpór S tak, aby pozostałe zdania były łącznie spełnialne. Na przykład, można użyć zanegowanej kwerendy jako zestawu wsparcia, zakładając, że pierwotna baza wiedzy jest spójna. (W końcu, jeśli nie jest spójny, to fakt, że zapytanie wynika z niego, jest bezsensowny.) Strategia zestawu wsparcia ma dodatkową zaletę, że generuje ukierunkowane na cel drzewa dowodów, które często są łatwe do zrozumienia dla ludzi.

ROZDZIELCZOŚĆ WEJŚCIOWA: W tej strategii każda rozdzielczość łączy jedno ze zdań wejściowych (z KB lub zapytania) z innym zdaniem. Dowód wykorzystuje tylko rozdzielczości wejściowe i ma charakterystyczny kształt pojedynczego „grzbietu” z pojedynczymi zdaniami łączącymi się na grzbiecie. Wyraźnie widać, że przestrzeń drzewek dowodowych o takim kształcie jest mniejsza niż przestrzeń wszystkich grafów dowodowych. W bazach wiedzy Horn, Modus Ponens jest rodzajem strategii rozwiązywania danych wejściowych, ponieważ łączy implikacje z oryginalnego KB z kilkoma innymi zdaniami. Nie jest więc niespodzianką, że rozdzielczość danych wejściowych jest kompletna dla baz wiedzy w formie Horn, ale niekompletna w ogólnym przypadku. Strategia rozdzielczości liniowej jest niewielkim uogólnieniem, które pozwala na rozwiązanie P i Q razem, jeśli P znajduje się w oryginalnym KB lub jeśli P jest przodkiem Q w drzewie dowodowym. Rozdzielczość liniowa jest zakończona.

SUBSUMPCJA: Metoda subsumcji eliminuje wszystkie zdania, które są podciągane przez (czyli bardziej szczegółowe niż) zdanie istniejące w KB. Na przykład, jeśli P(x) jest w KB, to nie ma sensu dodawanie P(A) i jeszcze mniej sensu dodawanie P(A) V Q(B) . Subsumowanie pomaga utrzymać małą KB, a tym samym pomaga utrzymać małą przestrzeń wyszukiwania.

Nauka: możemy ulepszyć dowodzenie twierdzenia, ucząc się na podstawie doświadczenia. Mając zbiór wcześniej udowodnionych twierdzeń, wytrenuj system uczenia maszynowego, aby odpowiedzieć na pytanie: mając zestaw przesłanek i cel do udowodnienia, jakie kroki dowodowe są podobne do kroków, które były skuteczne w przeszłości? System DEEPHOL  robi dokładnie to, wykorzystując głębokie sieci neuronowe do budowania modeli (zwanych osadzaniami) celów i przesłanek oraz wykorzystując je do dokonywania wyborów. Szkolenie może wykorzystywać jako przykłady zarówno dowody generowane przez ludzi, jak i komputery, zaczynając od zbioru 10 000 dowodów.

Żadna z metod wnioskowania opisanych do tej pory w tym rozdziale nie poradzi sobie z twierdzeniem postaci x = y bez dodatkowej pracy. Można zastosować trzy różne podejścia. Pierwszym z nich jest aksjomatyzacja równości – zapisanie zdań o relacji równości w bazy wiedzy. Musimy powiedzieć, że równość jest zwrotna, symetryczna i przechodnia, a także musimy powiedzieć, że możemy zastąpić równaniami równymi w dowolnym predykacie lub funkcji. Potrzebujemy więc trzech podstawowych aksjomatów, a następnie po jednym dla każdego predykatu i funkcji:

Biorąc pod uwagę te zdania, standardowa procedura wnioskowania, taka jak rozdzielczość, może wykonywać zadania wymagające wnioskowania o równości, takie jak rozwiązywanie równań matematycznych. Jednak te aksjomaty wygenerują wiele wniosków, z których większość nie będzie pomocna w dowodzie. Tak więc drugie podejście polega na dodawaniu reguł wnioskowania, a nie aksjomatów. Najprostsza zasada, demodulacja, przyjmuje klauzulę jednostkową x = y i pewną klauzulę α który zawiera termin x i daje nową klauzulę utworzoną przez podstawienie y za x w obrębie α. Działa, jeśli termin w α łączy się z ; nie musi być dokładnie równe x. Zauważ, że demodulacja jest kierunkowa; biorąc pod uwagę x = y , x zawsze jest zastępowany przez y, nigdy odwrotnie. Oznacza to, że demodulację można wykorzystać do uproszczenia wyrażeń za pomocą demodulatorów, takich jak z+0 = z lub z¹ = z . Jako inny przykład podano

możemy zakończyć demodulacją

Bardziej formalnie mamy

* DEMODULACJA: Dla dowolnych terminów x, y  i z, gdzie z pojawia się gdzieś w dosłownym m i gdzie  UNIFY(x,z) = θ

gdzie SUBST jest zwykłym podstawieniem listy wiążącej, a SUB(x,y,m) oznacza zastąpienie x przez y gdzieś w obrębie m . Reguła może być również rozszerzona o obsługę klauzul niejednostkowych, w których pojawia się znak równości:

* PARAMODULACJA: dla dowolnych wyrażeń x, y i z , gdzie występuje gdzieś w literze m , a gdzie , UNIFY(x,z) = θ

Na przykład z

mamy θ = UNIFY(F(A,y),F(x,B)) = {x/A , y/B} , i możemy zakończyć przez paramodulację zdania

Paramodulacja daje pełną procedurę wnioskowania dla logiki pierwszego rzędu z równością. Trzecie podejście obsługuje wnioskowanie o równości w całości w ramach rozszerzonego algorytmu unifikacji. Oznacza to, że terminy są unifikowalne, jeśli są równorzędne do udowodnienia przy pewnym podstawieniu, gdzie „dowieść” pozwala na wnioskowanie o równości. Na przykład terminy 1 + 2 i 2 + 1 zwykle nie są unifikowalne, ale algorytm unifikacji, który wie, że x + y = y + x może je ujednolicić za pomocą pustego podstawienia. Tego rodzaju unifikację równań można przeprowadzić za pomocą wydajnych algorytmów zaprojektowanych dla poszczególnych używanych aksjomatów (przemienność, asocjatywność itd.), a nie poprzez jawne wnioskowanie z tymi aksjomatami. Dowodzące twierdzeń przy użyciu tej techniki są ściśle związane z systemami CLP.