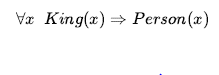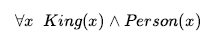Teraz, gdy zdefiniowaliśmy ekspresyjny język logiczny, nauczmy się go używać. W tej sekcji podajemy przykładowe zdania w kilku prostych domenach. W reprezentacji wiedzy domena to tylko część świata, o której chcemy wyrazić pewną wiedzę. Zaczniemy od krótkiego opisu interfejsu TELL/ASK dla baz wiedzy pierwszego rzędu. Następnie przyjrzymy się domenom relacji rodzinnych, liczb, zbiorów i list oraz światowi wumpusów.
Kontynuując przykład z poprzedniej części, załóżmy, że wierzymy, iż Richard ma dwóch braci, Johna i Geoffreya. Moglibyśmy napisać
ale to nie oddałoby całkowicie stanu rzeczy. Po pierwsze, to stwierdzenie jest prawdziwe w modelu, w którym Richard ma tylko jednego brata — musimy dodać Johna ≠ Geoffreya . Po drugie, zdanie nie wyklucza modeli, w których Richard ma o wiele więcej braci oprócz Johna i Geoffreya. Tak więc poprawne tłumaczenie „Bracia Richarda to John i Geoffrey” jest następujące:
To logiczne zdanie wydaje się o wiele bardziej kłopotliwe niż odpowiadające mu zdanie w języku angielskim. Ale jeśli nie przetłumaczymy poprawnie języka angielskiego, nasz logiczny system rozumowania będzie popełniał błędy. Czy możemy opracować semantykę, która pozwoli na bardziej bezpośrednie zdanie logiczne? Jedna z propozycji, która jest bardzo popularna w systemach bazodanowych, działa w następujący sposób. Po pierwsze, nalegamy, aby każdy stały symbol odnosił się do odrębnego obiektu – założenie o unikalnych nazwach. Po drugie, zakładamy, że zdania atomowe, o których nie wiadomo, że są prawdziwe, są w rzeczywistości fałszywe – założenie świata zamkniętego. Na koniec odwołujemy się do domknięcia domeny, co oznacza, że każdy model zawiera nie więcej elementów domeny niż te nazwane przez symbole stałe. Zgodnie z uzyskaną semantyką równanie rzeczywiście stwierdza, że Richard ma dokładnie dwóch braci, Johna i Geoffreya. Nazywamy tę semantykę bazy danych, aby odróżnić ją od standardowej semantyki logiki pierwszego rzędu. Semantyka baz danych jest również wykorzystywana w systemach programowania logicznego.
Pouczające jest rozważenie zestawu wszystkich możliwych modeli w ramach semantyki bazy danych. Rysunek przedstawia niektóre modele, począwszy od modelu bez krotek spełniających relację do modelu, przy czym wszystkie krotki spełniają relację. W przypadku dwóch obiektów istnieją cztery możliwe krotki dwuelementowe, więc istnieje 24 = 16 różnych podzbiorów krotek, które mogą spełnić relację. Tak więc jest w sumie 16 możliwych modeli – znacznie mniej niż nieskończenie wiele modeli dla standardowej semantyki pierwszego rzędu. Z drugiej strony semantyka bazy danych wymaga określonej wiedzy o tym, co zawiera świat.
Ten przykład podnosi ważną kwestię: nie ma jednej „poprawnej” semantyki dla logiki. Użyteczność każdej proponowanej semantyki zależy od tego, na ile zwięzła i intuicyjna wyraża ona rodzaje wiedzy, które chcemy zapisać, oraz od tego, jak łatwe i naturalne jest opracowanie odpowiednich reguł wnioskowania. Semantyka bazy danych jest najbardziej użyteczna, gdy jesteśmy pewni tożsamości wszystkich obiektów opisanych w bazie wiedzy i gdy mamy pod ręką wszystkie fakty; w innych przypadkach jest to dość niezręczne. Dla reszty zakładamy standardową semantykę, odnotowując przypadki, w których ten wybór prowadzi do nieporęcznych wyrażeń.
Logika pierwszego rzędu zawiera jeszcze jeden sposób tworzenia zdań atomowych, inny niż użycie predykatu i terminów, jak opisano wcześniej. Możemy użyć symbolu równości, aby wskazać, że dwa terminy odnoszą się do tego samego obiektu. Na przykład,
Father (John) = Henry
mówi, że przedmiot, do którego odnosi się Father (John) i obiekt, do którego odnosi się Henry, są tym samym. Ponieważ interpretacja ustala odniesienie dowolnego terminu, ustalenie prawdziwości zdania równości jest po prostu kwestią dostrzeżenia, że odniesienie tych dwóch terminów jest tym samym przedmiotem. Symbol równości może być użyty do określenia faktów dotyczących danej funkcji, tak jak właśnie zrobiliśmy w przypadku symbolu Ojca. Można go również używać z negacją, aby podkreślić, że dwa terminy nie są tym samym przedmiotem. Aby powiedzieć, że Richard ma co najmniej dwóch braci, napisalibyśmy
Zdanie
nie ma zamierzonego znaczenia. W szczególności dotyczy to modelu, gdzie Richard ma tylko jednego brata. Aby to zobaczyć, rozważ rozszerzoną interpretację – w której oba x i y są przypisane do króla Jana. Dodanie ¬(x = y) wyklucza takie modele. Notacja x ≠ y jest czasami używana jako skrót ¬(x = y).
Te dwa kwantyfikatory są w rzeczywistości ściśle ze sobą powiązane poprzez negację. Twierdzenie, że każdy nie lubi pasternaku jest tym samym, co twierdzenie, że nie istnieje ktoś, kto je lubi i vice versa:
Możemy pójść o krok dalej: „Każdy lubi lody” oznacza, że nie ma nikogo, kto nie lubi lodów:
Ponieważ ∀ tak naprawdę jest koniunkcją nad wszechświatem obiektów a ∃ jest alternatywą, nie powinno dziwić, że są one posłuszne regułom De Morgana. Reguły De Morgana dla zdań kwantyfikowanych i niekwantyfikowanych są następujące:
Tak więc tak naprawdę nie potrzebujemy zarówno ∀ i ∃ i , tak jak nie potrzebujemy tak naprawdę obu Λ i V . Jednak czytelność jest ważniejsza niż oszczędność, więc zachowamy oba kwantyfikatory.
Często będziemy chcieli wyrazić bardziej złożone zdania za pomocą wielu kwantyfikatorów. Najprostszy przypadek to taki, w którym kwantyfikatory są tego samego typu. Na przykład „Bracia są rodzeństwem” można zapisać jako
Kolejne kwantyfikatory tego samego typu można zapisać jako jeden kwantyfikator z kilkoma zmiennymi. Na przykład, aby powiedzieć, że rodzeństwo jest relacją symetryczną, możemy zapisać
W innych przypadkach będziemy mieli mieszanki. „Każdy kogoś kocha” oznacza, że dla każdej osoby jest ktoś, kogo ktoś kocha:
Z drugiej strony, aby powiedzieć „Jest ktoś, kogo wszyscy kochają”, piszemy
Dlatego bardzo ważna jest kolejność kwantyfikacji. Staje się to jaśniejsze, jeśli wstawimy nawiasy. ∀x(∃y Loves(x,y)) mówi, że każdy ma określoną właściwość, mianowicie właściwość, że kogoś kocha. Z drugiej strony ∃y (∀x Loves(x,y)) mówi, że ktoś na świecie ma szczególną właściwość, a mianowicie właściwość bycia kochanym przez wszystkich. Gdy dwa kwantyfikatory są używane z tą samą nazwą zmiennej, może powstać pewne zamieszanie. Rozważ zdanie
Tutaj x w Brother(Richard,x) jest skwantyfikowane egzystencjalnie. Zasada jest taka, że zmienna należy do najgłębszego kwantyfikatora, który o niej wspomina; wtedy nie będzie podlegał żadnej innej kwantyfikacji. Inny sposób myślenia o tym jest następujący: ∃x Brother(Richard,x) to zdanie o Richardzie (że ma brata), a nie o x; więc umieszczenie ∀x na zewnątrz nie ma żadnego efektu. Równie dobrze mogło zostać zapisane ∃z Brother(Richard,z). Ponieważ może to być źródłem nieporozumień, zawsze będziemy używać różnych nazw zmiennych z zagnieżdżonymi kwantyfikatorami.
Uniwersalna kwantyfikacja czyni stwierdzenia o każdym przedmiocie. Podobnie możemy wypowiedzieć się o jakimś przedmiocie bez nazywania go, używając kwantyfikatora egzystencjalnego. Aby powiedzieć na przykład, że król Jan ma koronę na głowie, piszemy
∃x wymawia się „Istnieje takie, które…” lub „Dla niektórych”. Intuicyjnie zdanie ∃x P mówi, że P jest prawdziwe dla przynajmniej jednego przedmiotu x. Dokładniej, ∃x P jest prawdziwe w danym modelu, jeśli P jest prawdziwe w co najmniej jednej rozszerzonej interpretacji, która przypisuje x do elementu domeny. Oznacza to, że przynajmniej jedno z poniższych jest prawdziwe:
Piąte stwierdzenie jest prawdziwe w modelu, więc oryginalne egzystencjalnie skwantyfikowane zdanie jest prawdziwe w modelu. Zauważ, że z naszej definicji zdanie to byłoby prawdziwe również w modelu, w którym król Jan nosił dwie korony. Jest to całkowicie zgodne z oryginalnym zdaniem „Król Jan ma koronę na głowie”. Tak jak => wydaje się być naturalnym spójnikiem używanym z ∀, Λ , jest naturalnym spójnikiem używanym z ∃ . Użycie Λ jako głównego łącznika z ∀ doprowadziło do zbyt silnego stwierdzenia w przykładzie z poprzedniej sekcji; używanie => z ∃ zwykle prowadzi do bardzo słabego stwierdzenia. Rozważ następujące zdanie
Na pierwszy rzut oka może to wyglądać na rozsądną interpretację naszego zdania. Stosując semantykę, widzimy, że zdanie mówi, że przynajmniej jedno z następujących stwierdzeń jest prawdziwe:
i tak dalej. Implikacja jest prawdziwa, jeśli zarówno przesłanka, jak i wniosek są prawdziwe, lub jeśli jego przesłanka jest fałszywa; więc jeśli Ryszard Lwie Serce nie jest koroną, to pierwsze twierdzenie jest prawdziwe i egzystencjalne jest spełnione. Zatem egzystencjalnie skwantyfikowane zdanie implikacyjne jest prawdziwe, gdy jakikolwiek obiekt nie spełnia przesłanki; stąd takie zdania naprawdę niewiele mówią.
Przypomnijmy sobie trudność, jaką mieliśmy z wyrażeniem ogólnych zasad w logice zdań. Reguły takie jak „Kwadraty sąsiadujące z wumpusem śmierdzą” i „Wszyscy królowie są osobami” to chleb powszedni logiki pierwszego rzędu. Pierwszym z nich zajmiemy się później. Druga zasada, „Wszyscy królowie są osobami”, jest napisana w logice pierwszego rzędu jako
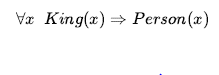
Uniwersalny kwantyfikator jest zwykle wymawiany „Dla wszystkich … ”. (Pamiętaj, że odwrócone A oznacza „wszystko”). Zatem zdanie mówi: „Dla wszystkich, jeśli jest królem, to x jest osobą”. Symbol x nazywa się zmienną. Zgodnie z konwencją, zmienne są małymi literami. Zmienna jest terminem samym w sobie i jako taka może również służyć jako argument funkcji – na przykład LeftLeg(x). Termin bez zmiennych nazywany jest terminem podstawowym.
Intuicyjnie, zdanie ∀x P , gdzie P jest dowolnym zdaniem logicznym, mówi, że jest prawdziwe dla każdego obiektu x. Dokładniej, ∀x P jest prawdziwe w danym modelu, jeśli P jest prawdziwe we wszystkich możliwych interpretacjach rozszerzonych zbudowanych z interpretacji podanej w modelu, gdzie każda interpretacja rozszerzona określa element domeny, do której się odnosi x.
Brzmi to skomplikowanie, ale tak naprawdę jest to tylko ostrożny sposób na określenie intuicyjnego znaczenia uniwersalnej kwantyfikacji. Rozważ model pokazany na rysunku i zamierzoną interpretację, która się z nim wiąże. Interpretację możemy rozszerzyć na pięć sposobów:
Zdanie uniwersalnie kwantyfikowane ∀x King(x) => Person(x) jest prawdziwe w oryginalnym modelu, jeśli zdanie King(x) => Person(x) jest prawdziwe w każdej z pięciu rozszerzonych interpretacji. Oznacza to, że zdanie powszechnie kwantyfikowalne jest równoważne stwierdzeniu następujących pięciu zdań:
Przyjrzyjmy się uważnie temu zestawowi twierdzeń. Ponieważ w naszym modelu król Jan jest jedynym królem, drugie zdanie stwierdza, że jest on osobą, jak byśmy mieli nadzieję. Ale co z pozostałymi czterema zdaniami, które wydają się zawierać twierdzenia dotyczące nóg i koron? Czy to część znaczenia słowa „Wszyscy królowie są osobami”? W rzeczywistości pozostałe cztery twierdzenia są prawdziwe w modelu, ale nie podawaj żadnych roszczeń co do cech osobowości nóg, koron, czy też Richarda. To dlatego, że żaden z tych obiektów nie jest królem. Patrząc na tabelę prawdy, widzimy, że implikacja jest prawdziwa zawsze, gdy jej założenie jest fałszywe – niezależnie od prawdziwości wniosku. Tak więc, stwierdzając zdanie powszechnie skwantyfikowane, co jest równoważne stwierdzeniu całej listy indywidualnych implikacji, w końcu stwierdzamy konkluzję reguły tylko dla tych przedmiotów, dla których przesłanka jest prawdziwa, i nie mówimy w ogóle o tych przedmiotach, dla których założenie jest fałszywe. Tak więc definicja tabeli prawdy okazuje się idealna do pisania ogólnych reguł za pomocą uniwersalnych kwantyfikatorów. Częstym błędem, popełnianym często nawet przez pilnych czytelników, którzy przeczytali ten paragraf kilka razy, jest użycie spójnika zamiast implikacji. Zdanie
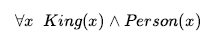
byłoby równoznaczne z twierdzeniem
i tak dalej. Oczywiście to nie oddaje tego, czego chcemy.
Kiedy już mamy logikę dopuszczającą obiekty, naturalne jest, że chcemy wyrażać właściwości całych kolekcji obiektów, zamiast wymieniać obiekty po nazwie. Pozwalają nam na to kwantyfikatory. Logika pierwszego rzędu zawiera dwa standardowe kwantyfikatory, zwane uniwersalnym (∀) i egzystencjalnym (∃).
[wp_ad_camp_1
Możemy używać spójników logicznych do konstruowania bardziej złożonych zdań, z taką samą składnią i semantyką jak w rachunku zdań. Oto cztery zdania, które są prawdziwe w modelu zgodnie z naszą zamierzoną interpretacją:
Teraz, gdy mamy terminy odnoszące się do obiektów i symbole predykatów odnoszące się do relacji, możemy je połączyć, aby stworzyć zdania atomowe, które stwierdzają fakty. Zdanie atomowe (lub w skrócie atom) składa się z symbolu predykatu, po którym opcjonalnie następuje lista terminów w nawiasach, takich jak
Brother(Richard,John)
Stwierdza to, zgodnie z zamierzoną interpretacją podaną wcześniej, że Ryszard Lwie Serce jest bratem króla Jana. Zdania atomowe mogą zawierać złożone terminy jako argumenty. Zatem,
Żonaty (Ojciec (Richard), Matka (John))
stwierdza, że ojciec Ryszarda Lwie Serce jest żonaty z matką króla Jana (znowu pod odpowiednią interpretacją).
Zdanie atomowe jest prawdziwe w danym modelu, jeśli relacja, do której odwołuje się symbol predykatu, zachodzi między przedmiotami, do których odwołują się argumenty.