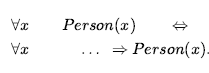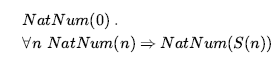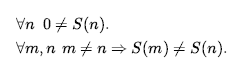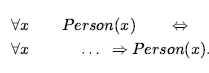Liczby są prawdopodobnie najbardziej żywym przykładem tego, jak wielką teorię można zbudować z malutkiego jądra aksjomatów. Opisujemy tutaj teorię liczb naturalnych lub nieujemnych liczb całkowitych. Potrzebujemy predykatu NatNum, który będzie prawdziwy dla liczb naturalnych; potrzebujemy jednego stałego symbolu, 0; i potrzebujemy jednego symbolu funkcji, S (następca). Aksjomaty Peano definiują liczby naturalne i dodawanie. Liczby naturalne są definiowane rekurencyjnie:
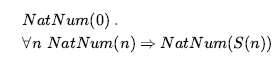
Oznacza to, że 0 jest liczbą naturalną, a dla każdego obiektu n , jeśli n jest liczbą naturalną, to S(n) jest liczbą naturalną. Więc liczby naturalne to 0, S(0), S(S(0)) , i tak dalej. Potrzebujemy również aksjomatów, aby ograniczyć funkcję następnika:
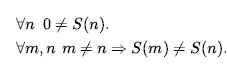
Teraz możemy zdefiniować dodawanie w terminach funkcji następnika
Pierwszy z tych aksjomatów mówi, że dodanie 0 do dowolnej liczby naturalnej m daje samo m. Zwróć uwagę na użycie symbolu funkcji binarnej „+” w terminie +(m,0) ; w zwykłej matematyce termin zostałby napisany m+0 przy użyciu notacji wrostkowej. (Notacja, której użyliśmy dla logiki pierwszego rzędu, nazywa się prefiksem). Aby ułatwić czytanie naszych zdań o liczbach, zezwalamy na użycie notacji infiksowej. Możemy również zapisać S(n) jako n+1 , więc drugi aksjomat staje się
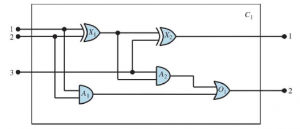
Aksjomat ten ogranicza dodawanie do wielokrotnego stosowania funkcji następcy. Użycie notacji infiksowej jest przykładem cukru składniowego, czyli rozszerzenia lub skrótu standardowej składni, który nie zmienia semantyki. Każde zdanie, w którym używa się cukru, może zostać „odcukrzone”, aby stworzyć równoważne zdanie w zwykłej logice pierwszego rzędu. Innym przykładem jest użycie nawiasów kwadratowych zamiast nawiasów, aby łatwiej było zobaczyć, który nawias lewy pasuje do nawiasu prawego. Jeszcze innym przykładem jest zwijanie się kwantyfikatorów: zastąpienie 
przez 
Kiedy już mamy dodawanie, łatwo jest zdefiniować mnożenie jako wielokrotne dodawanie, potęgowanie jako wielokrotne mnożenie, dzielenie liczb całkowitych i reszty, liczby pierwsze i tak dalej. Tak więc całą teorię liczb (w tym kryptografię) można zbudować z jednej stałej, jednej funkcji, jednego predykatu i czterech aksjomatów.
Dziedzina zbiorów ma również fundamentalne znaczenie dla matematyki, a także dla zdroworozsądkowego rozumowania. (W rzeczywistości możliwe jest zdefiniowanie teorii liczb w terminach teorii mnogości.) Chcemy móc reprezentować poszczególne zbiory, w tym zbiór pusty. Potrzebujemy sposobu na budowanie zbiorów z elementów lub operacji na innych zbiorach. Będziemy chcieli wiedzieć, czy element jest członkiem zbioru i będziemy chcieli odróżnić zbiory od obiektów, które nie są zbiorami.
Użyjemy normalnego słownictwa teorii mnogości jako cukru składniowego. Pusty zbiór to stała zapisana jako {} . Istnieje jeden orzecznik jednoargumentowy, Set, który jest prawdziwy dla zbiorów. Predykaty binarne to x ( jest x członkiem set s ) i s1 s2(zbiór s1 jest podzbiorem s2, prawdopodobnie równym s2 ). Funkcje binarne to s1 s2(przecięcie), s1 s2 (union) i Add(x,s)(zbiór wynikający z dodania elementu x do zbioru s ). Jeden z możliwych zestawów aksjomatów jest następujący:
- Jedyne zestawy to zestaw pusty oraz te wykonane przez dodanie czegoś do zestawu:
∀s Set(s) ⇔ (s ={}) ∨ (∃x, s2 Set(s2) ∧ s = Add(x, s2))
- Pusty zestaw nie zawiera żadnych dodanych elementów. Innymi słowy, nie ma sposobu, aby rozłożyć {} na mniejszy zestaw i element:
¬∃ x,s Add(x,s) = { }
- Dodanie elementu już w zestawie nie ma żadnego efektu:
∀x,s x ∈ s ⇔ s = Add(x,s)
- Jedynymi elementami zestawu są elementy, które zostały do niego dodane. Wyrażamy to rekurencyjnie, mówiąc, że jest członkiem wtedy i tylko wtedy, gdy jest równy pewnemu elementowi dodanemu do pewnego zbioru , gdzie albo jest taki sam jak albo jest członkiem :
∀x,s x ∈ s ⇔ ∃ y,s2 (s = Add(y,s2) ∧ (x = y ∨ x ∈ s2))
- Zbiór jest podzbiorem innego zbioru wtedy i tylko wtedy, gdy wszyscy członkowie pierwszego zbioru są członkami drugiego zbioru:
∀s1,s2 s1 ⊆ s2 ⇔ (∀x x ∈ s1 ⇒ x ∈ s2)
- Dwa zbiory są równe wtedy i tylko wtedy, gdy każdy jest podzbiorem drugiego:
∀s1,s2 (s1 = s2) ⇔ (s1 ⊆ s2 ∧ s2 ⊆ s1)
- Obiekt znajduje się na przecięciu dwóch zbiorów wtedy i tylko wtedy, gdy jest członkiem obu zbiorów:
∀x,s1,s2 x ∈ (s1 ∩ s2) ⇔ (x ∈ s1 ∧ x ∈ s2)
- Obiekt jest połączeniem dwóch zestawów wtedy i tylko wtedy, gdy jest członkiem jednego z zestawów:
∀x,s1,s2 x ∈ (s1 ∪ s2) ⇔ (x ∈ s1 ∨ x ∈ s2)
Listy są podobne do zestawów. Różnice polegają na tym, że listy są uporządkowane i ten sam element może pojawić się więcej niż raz na liście. Możemy użyć słownika Lispu dla list: Nil jest stałą listą bez elementów; Wady, Dołącz, Pierwszy i Reszta są funkcjami; a Find jest predykatem, który robi dla list to, co Member robi dla zbiorów. Lista jest predykatem, który jest prawdziwy tylko dla list. Podobnie jak w przypadku zestawów, często używa się cukru składniowego w zdaniach logicznych zawierających listy. Pusta lista to [ ]. Termin Cons(x,Nil) (tj. lista zawierająca element x, po którym następuje nic) jest zapisywany jako [x]. Lista kilku elementów, takich jak [A,B,C], odpowiada zagnieżdżonemu terminowi Cons(A,Cons(B,Cons(C,Nil)))
Aksjomaty definiują funkcję Matki i funkcję oraz predykaty Mąż, Mężczyzna, Rodzic, Dziadkowie i Rodzeństwo w kategoriach innych predykatów. Nasze definicje są „oddolne” w podstawowym zestawie predykatów (Dziecko, Kobieta itp.), w których ostatecznie definiuje się pozostałe.
Możemy wtedy powiedzieć, że obiekty mogą znajdować się tylko w jednym miejscu na raz:
przez 
Aksjomaty definiują funkcję Matki i funkcję oraz predykaty Mąż, Mężczyzna, Rodzic, Dziadkowie i Rodzeństwo w kategoriach innych predykatów. Nasze definicje są „oddolne” w podstawowym zestawie predykatów (Dziecko, Kobieta itp.), w których ostatecznie definiuje się pozostałe. Jest to naturalny sposób budowania reprezentacji domeny i jest analogiczny do sposobu budowania pakietów oprogramowania przez kolejne definicje podprogramów z pierwotnych funkcji bibliotecznych. Zauważ, że niekoniecznie istnieje unikalny zestaw predykatów pierwotnych; równie dobrze moglibyśmy użyć Rodzica zamiast Dziecka. W niektórych dziedzinach, jak pokazujemy, nie ma jednoznacznie identyfikowalnego zestawu podstawowego. Nie wszystkie logiczne zdania dotyczące domeny są aksjomatami. Niektóre są twierdzeniami – to znaczy wynikają z aksjomatów. Rozważmy na przykład twierdzenie, że rodzeństwo jest symetryczne:
