Pierwszym rozważanym przez nas przykładem jest dziedzina relacji rodzinnych lub pokrewieństwa. Ta domena obejmuje fakty, takie jak „Elizabeth jest matką Karola” i „Karol jest ojcem Williama” i zasady, takie jak „Babcia jest matką rodzica”. Oczywiście obiektami w naszej domenie są ludzie. Predykaty jednoargumentowe obejmują między innymi Male i Female. Relacje pokrewieństwa — rodzicielstwo, braterstwo, małżeństwo itd. — są reprezentowane przez predykaty binarne: rodzic, rodzeństwo, brat, siostra, dziecko, córka, syn, małżonek, żona, mąż, dziadek, wnuk, kuzyn, ciocia i wujek. Używamy funkcji Matki i Ojca, ponieważ każda osoba ma dokładnie jedną z nich, biologicznie (chociaż moglibyśmy wprowadzić dodatkowe funkcje dla matek adopcyjnych, matek zastępczych itp.). Możemy przejść przez każdą funkcję i orzeczenie, zapisując to, co wiemy, za pomocą innych symboli. Na przykład, czyjaś matka jest rodzicem, który jest kobietą:
Mąż to współmałżonek:
Rodzic i dziecko to odwrotne relacje:
Dziadek to rodzic Twojego rodzica:
Rodzeństwo to kolejne dziecko swojego rodzica:
Każde z tych zdań można traktować jako aksjomat domeny pokrewieństwa. Aksjomaty są powszechnie kojarzone z dziedzinami czysto matematycznymi — wkrótce zobaczymy niektóre aksjomaty liczb — ale są one potrzebne we wszystkich dziedzinach. Dostarczają podstawowych informacji faktycznych, z których można wyciągnąć użyteczne wnioski. Nasze aksjomaty pokrewieństwa są również definicjami; mają formę 
Aksjomaty definiują funkcję Matki i funkcję oraz predykaty Mąż, Mężczyzna, Rodzic, Dziadkowie i Rodzeństwo w kategoriach innych predykatów. Nasze definicje są „oddolne” w podstawowym zestawie predykatów (Dziecko, Kobieta itp.), w których ostatecznie definiuje się pozostałe. Jest to naturalny sposób budowania reprezentacji domeny i jest analogiczny do sposobu budowania pakietów oprogramowania przez kolejne definicje podprogramów z pierwotnych funkcji bibliotecznych. Zauważ, że niekoniecznie istnieje unikalny zestaw predykatów pierwotnych; równie dobrze moglibyśmy użyć Rodzica zamiast Dziecka. W niektórych dziedzinach, jak pokazujemy, nie ma jednoznacznie identyfikowalnego zestawu podstawowego. Nie wszystkie logiczne zdania dotyczące domeny są aksjomatami. Niektóre są twierdzeniami – to znaczy wynikają z aksjomatów. Rozważmy na przykład twierdzenie, że rodzeństwo jest symetryczne:
Czy to aksjomat czy twierdzenie? W rzeczywistości jest to twierdzenie, które logicznie wynika z aksjomatu definiującego rodzeństwo. Jeśli Pytamy bazę wiedzy o to zdanie, powinno ono zwrócić prawdę. Z czysto logicznego punktu widzenia baza wiedzy musi zawierać tylko aksjomaty, a nie twierdzenia, ponieważ twierdzenia nie powiększają zbioru wniosków wynikających z bazy wiedzy. Z praktycznego punktu widzenia twierdzenia są niezbędne do obniżenia kosztów obliczeniowych wyprowadzania nowych zdań. Bez nich system rozumowania musi za każdym razem zaczynać się od pierwszych zasad, podobnie jak fizyk musi na nowo wyprowadzać reguły rachunku różniczkowego dla każdego nowego problemu. Nie wszystkie aksjomaty są definicjami. Niektóre dostarczają bardziej ogólnych informacji o pewnych predykatach bez tworzenia definicji. Rzeczywiście, niektóre predykaty nie mają pełnej definicji, ponieważ nie wiemy wystarczająco dużo, aby je w pełni scharakteryzować. Na przykład nie ma oczywistego, ostatecznego sposobu na dokończenie zdania
Na szczęście logika pierwszego rzędu pozwala nam korzystać z predykatu Person bez całkowitego jego definiowania. Zamiast tego możemy napisać częściowe specyfikacje właściwości, które ma każda osoba, oraz właściwości, które czynią coś osobą:
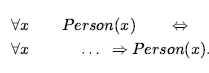
Aksjomaty mogą być również „po prostu zwykłymi faktami”, takimi jak Mężczyzna(Jim) i Małżonka(Jim,Laura). Takie fakty tworzą opisy konkretnych przypadków problemowych, umożliwiając udzielenie odpowiedzi na konkretne pytania. Jeśli wszystko pójdzie dobrze, odpowiedziami na te pytania będą twierdzenia wynikające z aksjomatów. Często okazuje się, że oczekiwane odpowiedzi nie nadchodzą – na przykład od Małżonki (Jim, Laura) oczekuje się (zgodnie z prawem wielu krajów), że będzie w stanie to wywnioskować ¬Spouse(George, Laura); ale nie wynika to z podanych wcześniej aksjomatów – nawet po dodaniu Jim ≠ George. To znak, że brakuje aksjomatu.