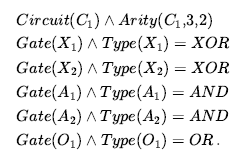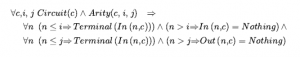Miesiąc: grudzień 2021

Jednym ze sposobów przeprowadzenia wnioskowania pierwszego rzędu jest przekształcenie bazy wiedzy pierwszego rzędu w logikę zdań i użycie wnioskowania zdań, co już wiemy. Pierwszym krokiem jest wyeliminowanie uniwersalnych kwantyfikatorów. Załóżmy na przykład, że nasza baza wiedzy zawiera standardowy aksjomat ludowy, że wszyscy chciwi królowie są źli:

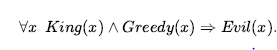
Z tego możemy wywnioskować dowolne z następujących zdań:

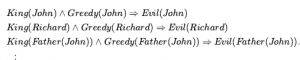
Ogólnie rzecz biorąc, reguła uniwersalnej instancji (w skrócie UI) mówi, że możemy wywnioskować dowolną encję uzyskaną przez zastąpienie termu podstawowego (terminu bez zmiennych) zmienną uniwersalnie kwantyfikowaną. Aby formalnie napisać regułę wnioskowania, posługujemy się pojęciem podstawień. SUBST(θ,α) oznacza wynik zastosowania podstawienia θ  do zdania α . Wtedy reguła jest zapisana :

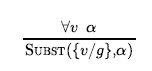
dla dowolnej zmiennej v i podstawowego warunku g. Na przykład trzy zdania podane wcześniej są otrzymywane z podstawieniami {x/John}, {x/Richard} , i {x/Father(John)}. Podobnie, zasada egzystencjalnej egzystencji zastępuje egzystencjalnie skwantyfikowaną zmienną pojedynczym nowym symbolem stałej. Formalne stwierdzenie jest następujące: dla każdego zdania α , zmiennej v i symbolu stałej k, który nie występuje nigdzie indziej w bazie wiedzy,

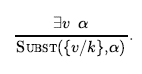
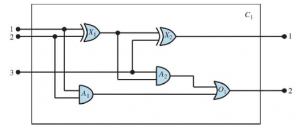
Na przykład ze zdania

możemy wywnioskować zdanie

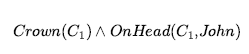
o ile C₁nie pojawia się w innym miejscu w bazie wiedzy. Zasadniczo zdanie egzystencjalne mówi, że istnieje jakiś obiekt spełniający warunek, a zastosowanie reguły egzystencjalnej konkretyzacji nadaje temu obiektowi nazwę. Oczywiście ta nazwa nie może już należeć do innego przedmiotu. Matematyka dostarcza dobrego przykładu: załóżmy, że odkrywamy, że istnieje liczba nieco większa niż 2,71828, która spełnia równanie d(x^y) / dy = x^y dla x . Możemy nadać temu numerowi nazwę e, ale błędem byłoby nadanie mu nazwy istniejącego obiektu, np. π . W logice nowa nazwa nazywa się stałą Skolema. Podczas gdy Uniwersalna Instancja może być zastosowana wiele razy do tego samego aksjomatu, aby wywołać wiele różnych konsekwencji, Egzystencjalna Instancja musi być zastosowana tylko raz, a następnie egzystencjalnie określone ilościowo zdanie może zostać odrzucone. Na przykład nie potrzebujemy już   po dodaniu zdania Kill(Murder, Victim)

Wprowadziliśmy logikę pierwszego rzędu, język reprezentacji, który jest znacznie potężniejszy niż logika zdań. Ważne punkty są następujące:

* Języki reprezentacji wiedzy powinny być deklaratywne, kompozycyjne, ekspresyjne, niezależne od kontekstu i jednoznaczne.

* Logiki różnią się zobowiązaniami ontologicznymi i epistemologicznymi.

* Podczas gdy logika zdaniowa zobowiązuje się jedynie do istnienia faktów, logika pierwszego rzędu zobowiązuje się do istnienia obiektów i relacji, a tym samym zyskuje moc wyrazu, właściwą dla dziedzin takich jak świat wumpusa i obwody elektroniczne.

* Zarówno logika zdań, jak i logika pierwszego rzędu mają trudności w przedstawianiu niejasnych zdań. Ta trudność ogranicza ich zastosowanie w dziedzinach wymagających osobistego osądu, takich jak polityka czy kuchnia.

* Składnia logiki pierwszego rzędu opiera się na składni logiki zdań. Dodaje terminy do reprezentowania obiektów i ma uniwersalne i egzystencjalne kwantyfikatory do konstruowania twierdzeń dotyczących wszystkich lub niektórych możliwych wartości zmiennych kwantyfikowanych.

* Możliwy świat lub model dla logiki pierwszego rzędu zawiera zbiór obiektów i interpretację, która odwzorowuje stałe symbole na obiekty, predykaty symboli na relacje między obiektami i symbole funkcji na funkcje na obiektach.

* Zdanie atomowe jest prawdziwe tylko wtedy, gdy relacja nazwana przez orzeczenie zachodzi między przedmiotami nazwanymi przez terminy. Interpretacje rozszerzone, które odwzorowują zmienne kwantyfikatorowe na obiekty w modelu, definiują prawdziwość zdań kwantyfikowalnych.

* Rozwijanie bazy wiedzy w logice pierwszego rzędu wymaga starannego procesu analizy domeny, wyboru słownictwa i kodowania aksjomatów wymaganych do obsługi pożądanych wniosków.

Jakie kombinacje wejść powodują, że pierwsze wyjście C₁ (bit sumy) ma wartość 0, a drugie wyjście C₁ (bit przeniesienia) ma wartość 1?

Odpowiedzi są podstawieniami zmiennych i1, i2 oraz i3 w taki sposób, że zdanie wynikowe jest zawarte w bazie wiedzy. ASKVARS da nam trzy takie podstawienia:

Jakie są możliwe zestawy wartości wszystkich zacisków dla obwodu sumatora?

To ostatnie zapytanie zwróci kompletną tabelę wejścia-wyjścia dla urządzenia, która może być użyta do sprawdzenia, czy faktycznie dodaje ono poprawnie swoje dane wejściowe. To jest prosty przykład weryfikacji obwodu. Możemy również wykorzystać definicję obwodu do budowy większych systemów cyfrowych, dla których można przeprowadzić ten sam rodzaj procedury weryfikacji. Wiele dziedzin jest podatnych na ten sam rodzaj ustrukturyzowanego rozwoju bazy wiedzy, w którym bardziej złożone koncepcje są definiowane obok prostszych konceptów.

Debuguj bazę wiedzy

Możemy zaburzać bazę wiedzy na różne sposoby, aby zobaczyć, jakie rodzaje błędnych zachowań się pojawiają. Załóżmy na przykład, że nie przeczytaliśmy sekcji 8.2. 8 i dlatego zapomnij stwierdzić, że 1 ≠ 0. Nagle system nie będzie w stanie udowodnić żadnych wyjść dla obwodu, z wyjątkiem przypadków wejściowych 000 i 110. Możemy wskazać problem, pytając o wyjścia każdej bramki. Na przykład możemy zapytać

co pokazuje, że nie są znane żadne wyjścia dla przypadków wejściowych 10 i 01. Następnie patrzymy na aksjomat dla bramek XOR, jak zastosowano do:

Jeśli wiadomo, że dane wejściowe to, powiedzmy, 1 i 0, to sprowadza się to do

Teraz problem jest oczywisty: system nie jest w stanie tego wywnioskować, Signal(Out(1,X₁)) = 1 więc musimy mu powiedzieć, że  1 ≠ 0

Obwód pokazany na rysunku jest zakodowany jako obwód C₁ z następującym opisem. Najpierw kategoryzujemy obwód i jego bramki składowe:

Następnie pokazujemy powiązania między nimi:

Jednym ze znaków, że mamy dobrą ontologię, jest to, że potrzebujemy tylko kilku ogólnych reguł, które można jasno i zwięźle określić. Oto wszystkie aksjomaty, których będziemy potrzebować:

1.Jeśli dwa zaciski są połączone, to mają ten sam sygnał:

2.Sygnał na każdym terminalu to 1 lub 0:

3.Połączenie jest przemienne:

4.Istnieją cztery rodzaje bramek:

5.Wyjście bramki AND ma wartość 0 wtedy i tylko wtedy, gdy którekolwiek z jej wejść ma wartość 0:

6.Wyjście bramki OR to 1 wtedy i tylko wtedy, gdy którekolwiek z jej wejść ma wartość 1:

7.Wyjście bramki XOR to 1 wtedy i tylko wtedy, gdy jej wejścia są różne:

8.Wyjście bramki NOT różni się od jej wejścia:

9.Bramki (oprócz NOT) posiadają dwa wejścia i jedno wyjście.

10.Obwód ma zaciski, aż do jego arności wejściowej i wyjściowej, i nic poza jego arnością:

11.Bramki, terminale i sygnały są różne.

12.Bramy to obwody.

Teraz wiemy, że chcemy rozmawiać o obwodach, zaciskach, sygnałach i bramkach. Następnym krokiem jest wybranie funkcji, predykatów i stałych do ich reprezentowania. Po pierwsze, musimy być w stanie odróżnić bramy od siebie i od innych obiektów. Każda bramka jest reprezentowana jako obiekt nazwany przez stałą, o której twierdzimy, że jest to bramka z, powiedzmy, Gate(X₁) . Zachowanie każdej bramki jest określone przez jej typ: jedna ze stałych AND,OR, XOR lub NOT. Ponieważ bramka ma dokładnie jeden typ, odpowiednia jest funkcja: Type(X₁) = XOR .

Obwody, podobnie jak bramki, są identyfikowane przez predykat: Circuit(C₁) .

Następnie rozważymy terminale, które są identyfikowane przez predykat Terminal(x). Obwód może mieć jeden lub więcej zacisków wejściowych i jeden lub więcej zacisków wyjściowych. Używamy tej funkcji In(1,X₁) do oznaczenia pierwszego zacisku wejściowego dla obwodu X₁. Podobną funkcję  Out(n,c)stosuje się dla zacisków wyjściowych. Funkcja Arity(c,i,j) mówi, że obwód c ma zaciski wejściowe i i wyjściowe j. Łączność między bramkami może być reprezentowana przez predykat Connected, który przyjmuje dwa terminale jako argumenty, jak Connected(Out(1,X₁),In(1,X₂) . Na koniec musimy wiedzieć, czy sygnał jest włączony, czy wyłączony. Jedną z możliwości jest użycie jednoargumentowego predykatu, On(t) który jest prawdziwy, gdy sygnał na terminalu jest włączony. Utrudnia to jednak zadawanie pytań typu „Jakie są wszystkie możliwe wartości sygnałów na zaciskach wyjściowych obwodu C₁?” Dlatego wprowadzamy jako obiekty dwie wartości sygnału, 1 i 0, reprezentujące odpowiednio „włączone” i „wyłączone”, oraz funkcję Signal(t), która oznacza wartość sygnału dla zacisku t.

Opracujemy ontologię i bazę wiedzy, które pozwolą nam wnioskować o obwodach cyfrowych w rodzaju pokazanych na rysunku .Śledzimy siedmioetapowy proces inżynierii wiedzy.

Zidentyfikuj pytania

Istnieje wiele zadań rozumowania związanych z obwodami cyfrowymi. Na najwyższym poziomie analizuje się funkcjonalność obwodu. Na przykład, czy obwód na rysunku 8.6 faktycznie dodaje się poprawnie? Jeśli wszystkie wejścia są wysokie, jakie jest wyjście bramki A2?

Istnieje wiele zadań rozumowania związanych z obwodami cyfrowymi. Na najwyższym poziomie analizuje się funkcjonalność obwodu. Na przykład, czy obwód na rysunku  faktycznie dodaje się poprawnie? Jeśli wszystkie wejścia są wysokie, jakie jest wyjście bramki A2? Interesujące są również pytania dotyczące struktury obwodu. Na przykład, jakie są wszystkie bramki podłączone do pierwszego zacisku wejściowego? Czy obwód zawiera pętle sprzężenia zwrotnego? To będą nasze zadania w tej sekcji. Istnieją bardziej szczegółowe poziomy analizy, w tym te związane z opóźnieniami czasowymi, obszarem obwodu, zużyciem energii, kosztami produkcji i tak dalej. Każdy z tych poziomów wymagałby dodatkowej wiedzy.

Zbierz odpowiednią wiedzę

Co wiemy o układach cyfrowych? Na nasze potrzeby składają się z drutów i bramek. Sygnały przepływają przewodami do zacisków wejściowych bramek, a każda bramka wytwarza sygnał na zacisku wyjściowym, który przepływa wzdłuż innego przewodu. Aby określić, jakie będą te sygnały, musimy wiedzieć, w jaki sposób bramki przekształcają swoje sygnały wejściowe. Istnieją cztery typy bramek: bramki AND, OR i XOR mają dwa zaciski wejściowe, a bramki NOT mają jeden. Wszystkie bramki mają jeden zacisk wyjściowy. Obwody, podobnie jak bramki, mają zaciski wejściowe i wyjściowe. Aby uzasadnić funkcjonalność i łączność, nie musimy mówić o samych przewodach, ścieżkach, którymi podążają, ani połączeniach, w których się łączą. Liczą się tylko połączenia między terminalami – możemy powiedzieć, że jeden terminal wyjściowy jest połączony z innym terminalem wejściowym, bez konieczności mówienia, co faktycznie je łączy. Inne czynniki, takie jak rozmiar, kształt, kolor lub koszt różnych komponentów, są dla nas nieistotne analizy. Gdyby naszym celem było coś innego niż weryfikacja projektów na poziomie bramek, ontologia byłaby inna. Na przykład, gdybyśmy byli zainteresowani debugowaniem uszkodzonych obwodów, prawdopodobnie dobrym pomysłem byłoby włączenie przewodów do ontologii, ponieważ wadliwy przewód może zaburzyć przepływający przez niego sygnał. Aby rozwiązać błędy czasowe, musielibyśmy uwzględnić opóźnienia bramek. Gdybyśmy byli zainteresowani zaprojektowaniem produktu, który byłby rentowny, wówczas istotny byłby koszt obwodu i jego szybkość w stosunku do innych produktów na rynku.

Projekty inżynierii wiedzy różnią się znacznie pod względem treści, zakresu i trudności, ale wszystkie takie projekty obejmują następujące etapy:

1. OKREŚL PYTANIA. Inżynier wiedzy musi określić zakres pytań, które baza wiedzy będzie wspierać, oraz rodzaje faktów, które będą dostępne dla każdej konkretnej instancji problemu. Na przykład, czy wumpusowa baza wiedzy musi mieć możliwość wyboru działań, czy wystarczy odpowiedzieć na pytania dotyczące zawartości środowiska? Czy fakty dotyczące czujnika będą zawierać aktualną lokalizację? Zadanie określi, jaka wiedza musi być reprezentowana, aby połączyć instancje problemów z odpowiedziami. Ten krok jest analogiczny do procesu PEAS dotyczącego projektowania agentów w rozdziale 2 .
2. ZBIERZ ODPOWIEDNIĄ WIEDZĘ. Inżynier wiedzy może już być ekspertem w danej dziedzinie lub może potrzebować współpracy z prawdziwymi ekspertami, aby wydobyć to, co wiedzą – w procesie zwanym pozyskiwaniem wiedzy. Na tym etapie wiedza nie jest reprezentowana formalnie. Chodzi o to, aby zrozumieć zakres bazy wiedzy określony przez zadanie oraz zrozumieć, jak faktycznie działa domena. W świecie wumpusa, który jest zdefiniowany przez sztuczny zestaw reguł, odpowiednia wiedza jest łatwa do zidentyfikowania. (Zauważ jednak, że definicja sąsiedztwa nie została wyraźnie podana w regułach świata Wumpus). weź pod uwagę rozproszenie pojemności i efekty skórne.
3. ZAJMIJ SIĘ SŁOWNIKIEM PREDYKATÓW, FUNKCJI I STAŁE. Oznacza to, że przetłumacz ważne koncepcje na poziomie domeny na nazwy poziomów logicznych. Wiąże się to z wieloma pytaniami dotyczącymi stylu inżynierii wiedzy. Podobnie jak styl programowania, może to mieć znaczący wpływ na ostateczny sukces projektu. Na przykład, czy zagłębienia powinny być reprezentowane przez obiekty, czy przez jednoargumentowy orzeczenie na kwadratach? Czy orientacja agenta powinna być funkcją czy predykatem? Czy lokalizacja wumpusa powinna zależeć od czasu? Po dokonaniu wyborów wynikiem jest słownictwo znane jako ontologia domeny. Słowo ontologia oznacza określoną teorię natury bytu lub istnienia. Ontologia określa, jakie rodzaje rzeczy istnieją, ale nie określa ich specyficznych właściwości i wzajemnych relacji.
4. ZAKODUJ OGÓLNĄ WIEDZĘ O DOMENIE. Inżynier wiedzy zapisuje aksjomaty dla wszystkich terminów słownikowych. To ustala (w miarę możliwości) znaczenie terminów, umożliwiając ekspertowi sprawdzenie treści. Często ten krok ujawnia nieporozumienia lub luki w słownictwie, które muszą naprawić, wracając do kroku 3 i powtarzając proces.
5. ZAKODUJ OPIS WYSTĄPIENIA PROBLEMU. Jeśli ontologia jest dobrze przemyślana, ten krok jest łatwy. Polega na pisaniu prostych zdań atomowych o wystąpieniach pojęć, które są już częścią ontologii. W przypadku agenta logicznego instancje problemu są dostarczane przez czujniki, podczas gdy „odcieleśniona” baza wiedzy otrzymuje zdania w taki sam sposób, jak tradycyjne programy otrzymują dane wejściowe.
6. ZADAWAJ ZAPYTANIA DO PROCEDURY WNIOSKOWANIA I UZYSKAJ ODPOWIEDZI. Tutaj jest nagroda: możemy pozwolić, aby procedura wnioskowania działała na aksjomatach i faktach specyficznych dla problemu, aby wyprowadzić fakty, które chcemy poznać. W ten sposób unikamy konieczności pisania algorytmu rozwiązania specyficznego dla aplikacji.
7. DEBUGUJ I OCENA BAZY WIEDZY. Niestety, odpowiedzi na pytania rzadko będą poprawne za pierwszym razem. Dokładniej, odpowiedzi będą poprawne dla bazy wiedzy w formie, w jakiej została napisana, zakładając, że procedura wnioskowania jest prawidłowa, ale nie będą tymi, których oczekuje użytkownik. Na przykład, jeśli brakuje aksjomatu, na niektóre zapytania nie będzie można odpowiedzieć z bazy wiedzy. Może dojść do znacznego procesu debugowania. Brakujące aksjomaty lub aksjomaty, które są zbyt słabe, można łatwo zidentyfikować, zauważając miejsca, w których łańcuch rozumowania niespodziewanie się zatrzymuje. Na przykład, jeśli baza wiedzy zawiera regułę diagnostyczną.

zamiast dwuwarunkowego, agent nigdy nie będzie w stanie udowodnić braku wumpuses. Błędne aksjomaty można zidentyfikować, ponieważ są to fałszywe stwierdzenia dotyczące świata. Na przykład zdanie

Bez zrozumienia otaczającego kontekstu nie można powiedzieć, czy przesunięcie powinno być pozycją, czy pozycją +1.

Kiedy dojdziesz do punktu, w którym nie ma oczywistych błędów w Twojej bazie wiedzy, kuszące jest ogłosić sukces. Ale o ile oczywiście nie ma błędów, lepiej formalnie ocenić swój system, uruchamiając go na zestawie testowym zapytań i mierząc, ile masz rację. Bez obiektywnego pomiaru zbyt łatwo jest przekonać samego siebie, że praca jest wykonana. Aby lepiej zrozumieć ten siedmioetapowy proces, zastosujemy go teraz do rozszerzonego przykładu – dziedziny obwodów elektronicznych.

Poprzednia sekcja ilustrowała użycie logiki pierwszego rzędu do reprezentacji wiedzy w trzech prostych dziedzinach. W tej sekcji opisano ogólny proces budowy bazy wiedzy – proces zwany inżynierią wiedzy. Inżynier wiedzy to ktoś, kto bada konkretną dziedzinę, uczy się, jakie koncepcje są w niej ważne i tworzy formalną reprezentację obiektów i relacji w tej domenie. Ilustrujemy proces inżynierii wiedzy w domenie obwodów elektronicznych. Przyjęte przez nas podejście jest odpowiednie do tworzenia specjalistycznych baz wiedzy, których dziedzina jest dokładnie określona i których zakres zapytań jest z góry znany. Bazy wiedzy ogólnego przeznaczenia, które obejmują szeroki zakres ludzkiej wiedzy i są przeznaczone do wspierania takich zadań, jak rozumienie języka naturalnego

Niektóre aksjomaty logiki zdań dla świata wumpus zostały podane wcześniej . Aksjomaty pierwszego rzędu w tej sekcji są znacznie bardziej zwięzłe, oddające w naturalny sposób dokładnie to, co chcemy powiedzieć. Przypomnij sobie, że agent wumpus otrzymuje wektor percepcji z pięcioma elementami. Odpowiednie zdanie pierwszego rzędu przechowywane w bazie wiedzy musi zawierać zarówno percept, jak i czas, w którym nastąpiło; w przeciwnym razie agent będzie zdezorientowany, kiedy zobaczy co. W krokach czasowych używamy liczb całkowitych. Typowym zdaniem percepcyjnym byłoby:

Tutaj Percept jest predykatem binarnym, a Stench i tak dalej są stałymi umieszczonymi na liście. Działania w świecie wumpus można przedstawić za pomocą terminów logicznych:

Aby określić, który z nich jest najlepszy, program agenta wykonuje zapytanie

który zwraca listę powiązań, taką jak . Program agenta może następnie powrócić jako działanie do wykonania. Surowe dane percepcyjne implikują pewne fakty dotyczące obecnego stanu. Na przykład:

i tak dalej. Reguły te przejawiają trywialną formę procesu rozumowania zwanego percepcją, którą szczegółowo przeanalizujemy w rozdziale 25 . Zwróć uwagę na kwantyfikację w czasie. W logice zdaniowej potrzebowalibyśmy kopii każdego zdania dla każdego kroku czasowego. Proste zachowanie „odruchowe” można również zaimplementować za pomocą skwantyfikowanych zdań implikacyjnych. Na przykład mamy

Biorąc pod uwagę poglądy i zasady z poprzednich akapitów, doprowadziłoby to do pożądanego wniosku BestAction(Grab,5)- jest to słuszne posunięcie. Przedstawiliśmy wejścia i wyjścia agenta; teraz nadszedł czas na reprezentowanie samego środowiska. Zacznijmy od przedmiotów. Oczywistymi kandydatami są kwadraty, doły i wumpus. Moglibyśmy nazwać każdy kwadrat – Square_1,2 i tak dalej — ale wtedy fakt, że  Square_1,2 i Square_1,3 są sąsiadujące, musiałby być faktem „dodatkowym” i potrzebowalibyśmy jednego takiego faktu dla każdej pary kwadratów. Lepiej jest użyć złożonego terminu, w którym wiersz i kolumna występują jako liczby całkowite; na przykład możemy po prostu użyć terminu listy [1,2]. Sąsiedztwo dowolnych dwóch kwadratów można zdefiniować jako

Moglibyśmy nazwać każdy dół, ale byłoby to niewłaściwe z innego powodu: nie ma powodu, aby rozróżniać doły. Łatwiej jest użyć jednoargumentowego predykatu Pit, który jest prawdziwy dla kwadratów zawierających wgłębienia. Wreszcie, ponieważ istnieje dokładnie jeden wumpus, stały Wumpus jest tak samo dobry jak orzeczenie jednoargumentowe (i być może bardziej dostojne z punktu widzenia wumpusa). Lokalizacja agenta zmienia się w czasie, dlatego piszemy At(Agent,s,t) w celu oznaczenia, że agent jest w punkcie kwadratowym s w czasie t . Możemy na zawsze naprawić wumpusa w określonej lokalizacji za pomocą . Możemy wtedy powiedzieć, że obiekty mogą znajdować się tylko w jednym miejscu na raz:

Biorąc pod uwagę jego aktualną lokalizację, agent może wywnioskować własności kwadratu z własności jego aktualnej percepcji. Na przykład, jeśli agent znajduje się na kwadracie i widzi powiew, to ten kwadrat jest przewiewny:

Warto wiedzieć, że kwadrat jest przewiewny, ponieważ wiemy, że doły nie mogą się poruszać. Zauważ, że Breezy nie ma argumentu dotyczącego czasu. Po odkryciu, które miejsca są przewiewne (lub śmierdzące) i, co bardzo ważne, nie przewiewne (lub nie śmierdzące), agent może wydedukować, gdzie są doły (i gdzie jest wumpus). Podczas gdy logika zdań wymaga oddzielnego aksjomatu dla każdego kwadratu i wymagałaby innego zestawu aksjomatów dla każdego geograficznego układu świata, logika pierwszego rzędu potrzebuje tylko jednego aksjomatu:

Podobnie w logice pierwszego rzędu możemy określić ilościowo w czasie, więc potrzebujemy tylko jednego aksjomatu stanu następcy dla każdego predykatu, a nie innej kopii dla każdego kroku czasowego.

Z tych dwóch przykładowych zdań widać, że sformułowanie logiki w rozdziale 7 . Czytelnik proszony jest o skonstruowanie analogicznych aksjomatów dla lokalizacji i orientacji agenta; w tych przypadkach aksjomaty dotyczą zarówno przestrzeni, jak i czasu. Podobnie jak w przypadku estymacji stanów zdań, agent może użyć logicznego wnioskowania z tego rodzaju aksjomatami, aby śledzić aspekty świata, które nie są bezpośrednio obserwowane.