Miesiąc: listopad 2021

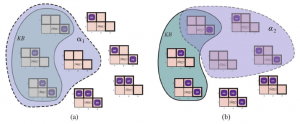
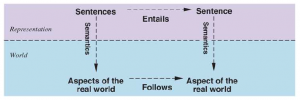
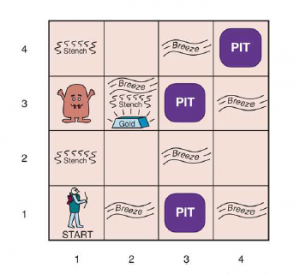
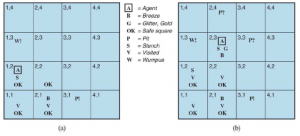
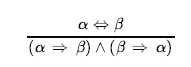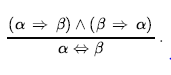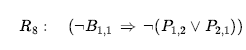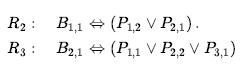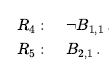Argumentowaliśmy, że opisane do tej pory reguły wnioskowania są prawidłowe, ale nie omawialiśmy kwestii kompletności algorytmów wnioskowania, które ich używają. Algorytmy wyszukiwania, takie jak iteracyjne wyszukiwanie pogłębiające, są kompletne w tym sensie, że znajdą dowolny osiągalny cel, ale jeśli dostępne reguły wnioskowania są nieodpowiednie, to cel nie jest osiągalny – nie ma dowodu, który używa tylko tych reguł wnioskowania. Na przykład, jeśli usuniemy dwuwarunkową zasadę eliminacji, dowód w poprzedniej sekcji nie przejdzie. Obecna sekcja wprowadza pojedynczą regułę wnioskowania, rozdzielczość, która daje kompletny algorytm wnioskowania w połączeniu z dowolnym kompletnym algorytmem wyszukiwania. Zaczynamy od prostej wersji reguły rozwiązywania w świecie wumpusa. Rozważmy kroki prowadzące do Rysunku 7.4(a): agent wraca z [2,1] do [1,1], a następnie przechodzi do [1,2], gdzie odczuwa smród, ale nie ma wiatru. Do bazy wiedzy dodajemy następujące fakty:

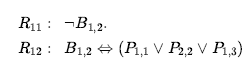
W tym samym procesie, który doprowadził R₁₀ do tego wcześniej, możemy teraz wyprowadzić brak wgłębień w [2,2] i [1,3] (pamiętaj, że [1,1] jest już znany jako bez wgłębień):

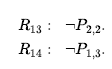
Możemy również zastosować dwuwarunkową eliminację do R₃ , a następnie Modus Ponens z R5 , aby uzyskać fakt, że w [1,1], [2,2] lub [3,1] jest dziura:

Teraz pojawia się pierwsze zastosowanie reguły rozstrzygania: literał in rozwiązuje z literałem in, aby dać rezolwentę

Po angielsku; jeśli w jednym z [1,1], [2,2] i [3,1] jest dół, a nie w [2,2], to jest w [1,1] lub [3,1]. Podobnie dosłowne ¬P_1,1 w R₁  rozwiązuje z dosłownym P_1,1 w R_1,6 dając

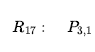
Po angielsku: jeśli jest dół w [1,1] lub [3,1], a nie w [1,1], to jest w [3,1]. Te dwa ostatnie kroki wnioskowania są przykładami reguły wnioskowania o rozdzielczości jednostki

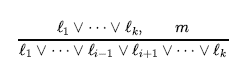
gdzie każdy l jest literałem, a l_i i m są literałami komplementarnymi (tj. jeden jest negacją drugiego). Tak więc reguła rozstrzygania jednostek przyjmuje klauzulę – alternatywę literałów – i literał i tworzy nową klauzulę. Zauważ, że pojedynczy literał może być postrzegany jako alternatywa jednego literału, znanego również jako klauzula jednostkowa. Regułę rozdzielczości jednostek można uogólnić do reguły pełnej rozdzielczości

gdzie l_i i m_j są literałami komplementarnymi. To mówi, że rozdzielczość przyjmuje dwie klauzule i tworzy nową klauzulę zawierającą wszystkie literały dwóch oryginalnych klauzul z wyjątkiem dwóch literałów uzupełniających. Na przykład mamy

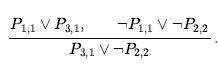
Jednocześnie można rozwiązać tylko jedną parę literałów uzupełniających. Na przykład możemy rozwiązać P i wydedukować ¬P

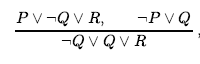
ale nie można rozwiązać jednocześnie na P i Q, aby wywnioskować R. Jest jeszcze jeden techniczny aspekt reguły rozstrzygania: wynikowa klauzula powinna zawierać tylko jedną kopię każdego literału. Usunięcie wielu kopii literałów nazywa się faktoringiem. Na przykład, jeśli rozwiązujemy (A V B) za pomocą (A V ¬B), otrzymujemy (A V A), co sprowadza A do samego faktoringu.

Słuszność reguły rozstrzygnięcia można łatwo dostrzec, biorąc pod uwagę dosłowne l_i, które jest komplementarne do dosłownego m_j w drugiej klauzuli. Jeśli li jest prawdziwe, to m_j jest fałszywe, a zatem musi być prawdziwe, ponieważ jest dane. Jeśli l_i jest fałszywe, to musi być prawdziwe, ponieważ .Teraz l_i jest prawda lub fałsz, więc jeden lub drugi z tych wniosków jest słuszny – dokładnie tak, jak stanowi reguła rozstrzygania. Bardziej zaskakujące w regule rozstrzygającej jest to, że stanowi ona podstawę rodziny kompletnych procedur wnioskowania. Dowód twierdzenia oparty na rozdzielczości może, dla dowolnych zdań i logiki zdań, zdecydować, czy

Spójna forma normalna

Reguła rozwiązywania dotyczy tylko klauzul (czyli alternatywy literałów), więc wydaje się, że dotyczy tylko baz wiedzy i zapytań składających się z klauzul. Jak zatem może prowadzić do kompletnej procedury wnioskowania dla całej logiki zdań? Odpowiedź brzmi, że każde zdanie logiki zdań jest logicznie równoważne koniunkcji zdań. Mówi się, że zdanie wyrażone jako koniunkcja zdań jest w spójnej formie normalnej lub CNF. Opiszemy teraz procedurę konwersji na CNF. Procedurę ilustrujemy zamieniając zdanie B1,1 ⇔  (P,1,2 V  _2,1)na CNF. Kroki są następujące:

1. Wyeliminuj ⇔ , zastępując α ⇔ β z (α ⇔  β) Λ ( β ⇔ α)

2. Wyeliminuj  ⇒ , zastępując (α ⇒ β) z ¬α V β:

3. CNF wymaga ¬, aby pojawiać się tylko w literach, więc „poruszamy się ¬ do wewnątrz” poprzez wielokrotne zastosowanie następujących równoważności :

 ¬(¬α) ≡ α (eliminacja podwójnej negacji)

¬(α Λ β) ≡ (¬α V ¬β) (De Morgan)

¬(α V β) ≡ (¬α Λ ¬β) (De Morgan)

W tym przykładzie wymagamy tylko jednego zastosowania ostatniej reguły:

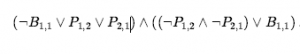
4. Teraz mamy zdanie zawierające zagnieżdżone Λ i V operatory zastosowane do literałów. Stosujemy prawo dystrybucji, rozprowadzając V i Λ tam, gdzie to możliwe.

Pierwotne zdanie jest teraz w CNF jako połączenie trzech klauzul. Jest znacznie trudniejszy do odczytania, ale może być wykorzystany jako dane wejściowe do procedury rozwiązywania problemów.

W tej sekcji omówiono reguły wnioskowania, które można zastosować w celu uzyskania dowodu — łańcucha wniosków prowadzących do pożądanego celu. Najbardziej znana reguła nazywa się Modus Ponens (łac. tryb, który potwierdza) i jest zapisana:

α⇒β , α / β

Notacja oznacza, że ilekroć podane są jakiekolwiek zdania postaci α ⇒  β  i  α są dane, to zdanie β można wywnioskować. Na przykład, jeśli (WumpusAhead ∧ WumpusAlive) ⇒  Shoot i (WumpusAhead ∧WumpusAlive)  można wywnioskować Shoot. Inną przydatną regułą wnioskowania jest I-Eliminacja, która mówi, że z koniunkcji można wywnioskować dowolną z koniunkcji:

α Λ β / α

Na przykład z(WumpusAhead ∧WumpusAlive) , WumpusAlive można wywnioskować. Rozważając możliwe wartości prawdy α i β, można łatwo wykazać raz na zawsze, że Modus Ponens i And-Elimination są słuszne. Reguły te mogą być następnie stosowane w dowolnych konkretnych przypadkach, w których mają zastosowanie, generując solidne wnioskowania bez konieczności wyliczania modeli. Wszystkie logiczne równoważności mogą być użyte jako reguły wnioskowania. Na przykład równoważność dwuwarunkowej eliminacji daje dwie reguły wnioskowania

i

Nie wszystkie reguły wnioskowania działają w obu kierunkach. Na przykład nie możemy uruchomić Modus Ponens w przeciwnym kierunku, aby uzyskać α ⇒ β i α z β.  Zobaczmy, jak te reguły wnioskowania i równoważności można wykorzystać w świecie wumpusa. Zaczynamy od bazy wiedzy zawierającej R₁ poprzez  R₅ i pokazujemy jak udowodnić ¬P_1,2, czyli nie ma dołu w [1,2]:

1. Zastosuj dwuwarunkową eliminację R₂, aby uzyskać

2. Zastosuj I –Eeliminację R₆, aby uzyskać

3. Logiczna równoważność dla przeciwstawnych daje

4. Zastosuj Modus Ponens za pomocą R₈ i percept R₄ (tj. ¬B1,2 ), aby uzyskać

5. Zastosuj regułę De Morgana, podając wniosek

Oznacza to, że ani [1,2] ani [2,1] nie zawiera dołu.

Każdy z algorytmów wyszukiwania w Rozdziale 3 może być użyty do znalezienia sekwencji kroków, która stanowi dowód taki jak ten. Wystarczy zdefiniować problem dowodowy w następujący sposób:

STAN POCZĄTKOWY: początkowa baza wiedzy.

AKCJE: zestaw akcji składa się ze wszystkich reguł wnioskowania zastosowanych do wszystkich zdań, które pasują do górnej połowy reguły wnioskowania.

WYNIK: wynikiem działania jest dodanie zdania w dolnej połowie reguły wnioskowania.

CEL: cel to stan, który zawiera zdanie, które próbujemy wędrować.

Poszukiwanie dowodów jest więc alternatywą dla wyliczania modeli. W wielu praktycznych przypadkach znalezienie dowodu może być bardziej efektywne, ponieważ dowód może zignorować nieistotne twierdzenia, bez względu na to, ile ich jest. Na przykład dowód przed chwilą prowadzący do ¬P_1,2 Λ ¬P_2,1 nie wspomina o zdaniach B_2,1, P_1,1, P_2,2 lub P_3,1. Można je zignorować, ponieważ zdanie celu, P_1,2 , pojawia się tylko w zdaniu R₂ ; pojawiają się tylko w R₄ i R₂ tak  więc R₁, R₃ i R₅ nie mają wpływu na dowód. To samo miałoby miejsce, nawet gdybyśmy dodali milion zdań do bazy wiedzy; z drugiej strony prosty algorytm tabeli prawdy zostałby przytłoczony wykładniczą eksplozją modeli. Ostatnią właściwością systemów logicznych jest monotoniczność, która mówi, że zbiór zdań pociągających za sobą może się powiększać tylko w miarę dodawania informacji do bazy wiedzy. Dla dowolnych zdań α i β,

Załóżmy na przykład, że baza wiedzy zawiera dodatkowe twierdzenie β stwierdzające, że na świecie jest dokładnie osiem dołów. Ta wiedza może pomóc agentowi wyciągnąć dodatkowe wnioski, ale nie może unieważnić żadnego wniosku, który został już wywnioskowany przez α – takiego jak wniosek, że nie ma dołków w [1,2]. Monotoniczność oznacza, że reguły wnioskowania mogą być stosowane zawsze, gdy w bazie wiedzy zostaną znalezione odpowiednie przesłanki – wniosek z reguły musi nastąpić niezależnie od tego, co jeszcze znajduje się w bazie wiedzy.

Do tej pory pokazaliśmy, jak wyznaczać wnioskowanie przez sprawdzanie modeli: wyliczając modele i pokazując, że zdanie musi obowiązywać we wszystkich modelach. W tym podrozdziale pokazujemy, w jaki sposób można przeprowadzić wywodzenie przez dowodzenie twierdzeń – zastosowanie reguł wnioskowania bezpośrednio do zdań w naszej bazie wiedzy w celu skonstruowania dowodu pożądanego zdania bez konsultacji z modelami. Jeśli liczba modeli jest duża, ale długość dowodu jest krótka, to dowodzenie twierdzenia może być bardziej efektywne niż sprawdzanie modelu. Zanim zagłębimy się w szczegóły algorytmów dowodzenia twierdzeń, będziemy potrzebować kilku dodatkowych pojęć związanych z wnioskowaniem. Pierwsza koncepcja to równoważność logiczna: dwa zdania α i β są logicznie równoważne, jeśli są prawdziwe w tym samym zbiorze modeli. Zapiszemy to jako  α ≡ β (Zauważ, że ≡ służy do wyrażania twierdzeń o zdaniach, podczas gdy  jest używane jako część zdania.) Na przykład możemy łatwo pokazać (używając tabel prawdy), że P Λ Q i Q Λ P są logicznie równoważne. Te równoważności odgrywają w logice tę samą rolę, co tożsamości arytmetyczne w zwykłej matematyce. Alternatywna definicja równoważności jest następująca: dowolne dwa zdania α i β są równoważne wtedy i tylko wtedy, gdy każde z nich pociąga za sobą drugie:

α ≡ β jeśli i tylko jeśli α |= β i β |= α

Drugim pojęciem, którego będziemy potrzebować, jest zasadność. Zdanie jest ważne, jeśli jest prawdziwe we wszystkich modelach. Na przykład ważne jest zdanie P V ¬P. Prawidłowe zdania są również znane jako tautologie – są z konieczności prawdziwe. Ponieważ zdanie Prawda jest prawdziwe we wszystkich modelach, każde poprawne zdanie jest logicznie równoważne z Prawdą. Jakie są dobre zdania? Z naszej definicji implikacji możemy wyprowadzić twierdzenie o dedukcji, które było znane starożytnym Grekom:

Dla dowolnych zdań α i β, (α  |-  β) wtedy i tylko wtedy, gdy zdanie (α ⇒ β) zdanie jest ważne.

Ostatnią koncepcją, której będziemy potrzebować, jest satysfakcja. Zdanie jest spełnialne, jeśli jest prawdziwe w jakimś modelu lub jest przez niego spełnione. Na przykład podana wcześniej baza wiedzy (R₁ Λ R₂ Λ R₃ Λ R₄ Λ R₅) jest zadowalająca, ponieważ istnieją trzy modele, w których jest ona prawdziwa. Spełnialność można sprawdzić, wyliczając możliwe modele, aż do znalezienia jednego, który spełnia zdanie. Problem określania spełnialności zdań w logice zdań – problem SAT – był pierwszym problemem, który okazał się NPzupełny. Wiele problemów w informatyce to tak naprawdę problemy spełnialności.

Trafność i spełnialność są oczywiście ze sobą powiązane: α jest poprawne, jeśli ¬α nie spełnia; przeciwnie, α jest spełnione jeśli ¬α jest nieważne. Mamy też następujący użyteczny wynik:

α |= β wtedy i tylko wtedy gdy zdanie (α Λ ¬β) jest niespełnione

Udowodnienie β z α  poprzez sprawdzenie niespełnienia (α Λ ¬β)  dokładnie odpowiada standardowej matematycznej technice dowodowej reductio ad absurdum (dosłownie „redukcja do rzeczy absurdalnej”). Nazywa się to również dowodem przez obalanie lub dowodem przez sprzeczność. Zakłada się, że zdanie β jest fałszywe i pokazuje, że prowadzi to do sprzeczności ze znanymi aksjomatami α. Ta sprzeczność jest dokładnie tym, co oznacza stwierdzenie, że zdanie (α Λ ¬β) jest niezadowalające.

Naszym celem jest teraz zdecydować, czy KB|= α za jakieś zdanie α. Na przykład, ¬P_1,2 wiąże się z naszym KB ? Nasz pierwszy algorytm wnioskowania to podejście polegające na sprawdzaniu modelu, które jest bezpośrednią implementacją definicji wnioskowania: należy wyliczyć modele i sprawdzić, czy  α jest prawdziwy w każdym modelu, w którym KB jest prawdziwy. Modele to przypisania prawdy lub fałszu do każdego symbolu zdania. Wracając do naszego przykładu wumpus-world, odpowiednie symbole zdań to B_1,1,B_2,1 ,P_1,1 ,P_1,2 ,P_2,2, i P_3,1 . Z siedmioma symbolami, istnieje 2⁷ = 128 możliwych modeli; w trzech z nich KB jest prawdą. W tych trzech modelach ¬P_1,2  to prawda, stąd nie ma wgłębienia w [1,2]. Z drugiej strony P_2,2jest prawdziwe w dwóch z trzech modeli, a fałszywe w jednym, więc nie możemy jeszcze stwierdzić, czy w [2,2] jest dół.

Ogólny algorytm decydowania o wynikaniu w logice zdań pokazano na poniżej. Jak algorytm BACKTRACKING-SEARCH, TT-ENTAILS? wykonuje rekurencyjne wyliczenie skończonej przestrzeni przypisań do symboli. Algorytm jest poprawny, ponieważ bezpośrednio implementuje definicję implikacji, i kompletny, ponieważ działa dla każdego KB i  α zawsze się kończy – jest tylko skończenie wiele modeli do zbadania.

Oczywiście „skończenie wiele” nie zawsze oznacza „niewiele”. Jeśli KB i  α zawierają symbole we wszystkich, to istnieją 2ⁿ modele. Zatem złożoność czasowa algorytmu wynosi O(2ⁿ). (Złożoność przestrzenna to tylko O(n) ponieważ wyliczenie jest na pierwszym miejscu.) W dalszej części tego pokażemy algorytmy, które w wielu przypadkach są znacznie wydajniejsze. Niestety, wywodzenie zdań jest co-NP-zupełnych (tj. prawdopodobnie nie łatwiejsze niż NP-zupełne), więc każdy znany algorytm wnioskowania dla logiki zdań ma złożoność najgorszego przypadku, która jest wykładnicza pod względem wielkości danych wejściowych.

---

Teraz, gdy zdefiniowaliśmy semantykę logiki zdań, możemy zbudować bazę wiedzy dla świata wumpusów. Skupiamy się najpierw na niezmiennych aspektach świata wumpus, pozostawiając zmienne aspekty na późniejszą sekcję. Na razie potrzebujemy następujących symboli dla każdej lokalizacji |x,y|:

P_x,y jest prawdziwe, jeśli jest  dół w |x,y| .

W_x,y jest prawdziwe, jeśli jest wumpus w |x,y| , martwy lub żywy.

B_x,y jest prawdziwe, jeśli jest sprzeczność w |x,y| .

S_x,y jest prawdziwe, jeśli jest smród w |x,y|.

L_x,y jest prawdziwe, jeśli agent znajduje się w lokalizacji |x,y| .

Zdania, które piszemy, wystarczą do wyprowadzenia ¬P_1,2  (nie ma dołu w [1,2]). Każde zdanie oznaczamy etykietą R_i, aby móc się do niego odnieść:

• W [1,1] nie ma dołu:

R1 : ¬P_1,1

Pole jest sprzeczne  wtedy i tylko wtedy, gdy na sąsiednim polu znajduje się dół. To musi być podane dla każdego kwadratu; na razie uwzględniamy tylko odpowiednie kwadraty:

Poprzednie zdania są prawdziwe we wszystkich światach Wumpus. Teraz uwzględniamy percepcje bryzy dla pierwszych dwóch odwiedzonych kwadratów w konkretnym świecie, w którym znajduje się agent

Po określeniu składni logiki zdań określamy teraz jej semantykę. Semantyka określa zasady ustalania prawdziwości zdania w odniesieniu do określonego modelu. W logice zdań model po prostu ustala wartość prawdy – prawdę lub fałsz – dla każdego symbolu zdania. Na przykład, jeśli zdania w bazie wiedzy wykorzystują symbole zdań P_1,2, P_2,2 i P_3,1 , to jednym z możliwych modeli jest

Z trzema symbolami propozycji, istnieje 2³ = 8 możliwych modeli – dokładnie tych przedstawionych na rysunku . Zauważ jednak, że modele są obiektami czysto matematycznymi, bez konieczności połączenia ze światami wumpusa P_1,2. jest tylko symbolem; może to oznaczać „jest dół w [1,2]” lub „Jestem w Paryżu dzisiaj i jutro”. Semantyka logiki zdań musi określać, jak obliczyć wartość logiczną dowolnego zdania przy danym modelu. Odbywa się to rekurencyjnie. Wszystkie zdania są zbudowane ze zdań atomowych i pięciu spójników; dlatego musimy określić, jak obliczyć prawdziwość zdań atomowych i jak obliczyć prawdziwość zdań utworzonych z każdym z pięciu spójników. Zdania atomowe są łatwe:

• Prawda jest prawdą w każdym modelu, a fałsz jest fałszem w każdym modelu.
• Wartość logiczną każdego innego symbolu zdaniowego należy podać bezpośrednio w modelu. Na przykład w podanym wcześniej modelu m₁ P_1,2 jest fałszywe.

Dla zdań złożonych mamy pięć reguł, które obowiązują dla dowolnych podzdań P i Q (atomowych lub złożonych) w dowolnym modelu m (tu „iff” oznacza „jeśli i tylko wtedy”):

• ¬P jest prawdziwe jeśli jest fałszywe w m .
• P Λ Q jest prawdziwe w przypadku obu P i Q są prawdziwe w m .
• P V Q jest prawdziwe, jeśli albo P jest prawdziwe, albo jest prawdziwe w m .
• P ⇒ Q jest prawdziwe, chyba że P jest prawdziwe a Q fałszywe w m .
• P ⇔ Q jest prawdziwe jeśli P i Q i obie są prawdziwe lub obie fałszywe w m .

Reguły mogą być również wyrażone za pomocą tablic prawdy, które określają wartość logiczną zdania złożonego dla każdego możliwego przypisania wartości logicznych do jego składników. Tabele prawdy dla pięciu spójników przedstawiono poniżej

Z tych tabel można obliczyć wartość logiczną dowolnego zdania s w odniesieniu do dowolnego modelu  m za pomocą prostej oceny rekurencyjnej. Na przykład zdanie ¬P_1,2 Λ  (P_2,2  V  P_3,1) , oceniane w m₁ , daje true  Λ  (false  V true) = true Λ true = true.

Tabele prawdy dla „i”, „lub” i „nie” są zgodne z naszymi intuicjami dotyczącymi angielskich słów. Głównym punktem możliwego zamieszania jest to, że P V Q jest prawdziwe, gdy P jest prawdziwe, Q jest prawdziwe lub oba. Inny spójnik, zwany „wyłącznym lub” (w skrócie „xor”), daje fałsz, gdy oba rozłączniki są prawdziwe. Nie ma zgody co do symbolu wyłączności lub; niektóre opcje to V lub ≠ lub ⊕   .

Tabela prawdy dla ⇒   może nie do końca pasować do intuicyjnego rozumienia „P implikuje Q ” lub „P jeśli to Q”. Po pierwsze, logika zdań nie wymaga żadnego związku przyczynowego ani relewancji między P i Q. Zdanie „5 jest nieparzyste oznacza, że ​​Tokio jest stolicą Japonii” jest prawdziwym zdaniem logiki zdań (przy normalnej interpretacji), mimo że jest to zdecydowanie dziwne zdanie. Innym powodem do nieporozumień jest to, że każda implikacja jest prawdziwa, gdy jej poprzednik jest fałszywy. Na przykład „5 oznacza nawet, że Sam jest mądry” jest prawdziwe, niezależnie od tego, czy Sam jest mądry. Wydaje się to dziwne, ale ma sens, jeśli pomyślisz, że „P ⇒ Q” mówi: „Jeśli P to prawda, to twierdzę, że Q to prawda; w przeciwnym razie nie wysuwam żadnych roszczeń”. Jedynym sposobem, aby to zdanie było fałszywe, jest stwierdzenie, czy P jest prawdziwe, ale Q jest fałszywe. Dwuwarunkowe, P ⇔  Q , jest prawdziwe, gdy oba P ⇒Q i  Q ⇒  P są prawdziwe. W języku angielskim często zapisuje się to jako „ P wtedy i tylko wtedy, gdy Q ”. Wiele zasad świata wumpusa najlepiej pisze się przy użyciu ⇔  . Na przykład, pole jest przewiewne, jeśli sąsiednie pole ma zagłębienie, a pole jest przewiewne tylko wtedy, gdy sąsiednie pole ma zagłębienie. Więc potrzebujemy dwuwarunkowego,

gdzie B1,1 oznacza, że ​​w [1,1] jest sprzeczność.

Składnia logiki zdań definiuje dopuszczalne zdania. Zdania atomowe składają się z jednego symbolu zdania. Każdy taki symbol oznacza propozycję, która może być prawdziwa lub fałszywa. Używamy symboli, które zaczynają się od dużej litery i mogą zawierać inne litery lub indeksy, na przykład: P ,Q , R ,W_1,3 i FacingEast. Nazwy są arbitralne, ale często są wybierane tak, aby miały pewną wartość mnemoniczną – używamy W_1,3 do oznaczenia twierdzenia, że wumpus jest w [1,3]. (Pamiętaj, że symbole takie jak W_1,3 są atomowe, tj. W, 1 i 3 nie są znaczącymi częściami symbolu.) Istnieją dwa symbole zdań o stałych znaczeniach: Prawda to zawsze prawdziwe zdanie, a False to zawsze fałszywe propozycja. Zdania złożone są konstruowane z prostszych zdań, przy użyciu nawiasów i operatorów zwanych spójnikami logicznymi. W powszechnym użyciu jest pięć łączników:

¬ nie). Zdanie takie jak ¬W_1,3 nazywa się negacją W1,3. Literał to albo zdanie atomowe (dosłowny literał) albo zanegowane zdanie atomowe (dosłowny ujemny).

Λ (oraz). Zdanie, którego spójnikiem głównym jest , takie jak W_1,3 Λ P_3,1 , nazywa się spójnikiem; jego części są koniunkcjami. (Λ Wygląda jak „A” dla „AND”)

V (lub). Zdanie, którego głównym spójnikiem jest V , takie jak (W_1,3 Λ P_3,1  ) V W_2,2, jest alternatywą; jego części są rozłączne – w tym przykładzie (W_1,3 Λ P_3,1  ) i W_2,2 .

⇒ (implikuje). Zdanie takie jak (W_1,3 Λ P_3,1  )  ¬W_2,2   jest nazywane implikacją (lub warunkiem). Jego przesłanką lub poprzednikiem jest (W_1,3 Λ P_3,1 ) , a jego zakończeniem lub następstwem jest  ¬W_2,2   . Implikacje są również znane jako reguły lub instrukcje if-then. Symbol implikacji jest czasami pisany w innych księgach, jako ⊃  lub →

⇔(wtedy i tylko wtedy gdy). Zdanie jest dwuwarunkowe.

Rysunek przedstawia formalną gramatykę logiki zdań. Gramatyka BNF jest wzbogacona o listę pierwszeństwa operatorów, aby usunąć niejednoznaczność, gdy używanych jest wiele operatorów. Operator „nie” (¬) ma najwyższy priorytet, co oznacza, że w zdaniu ¬A Λ B ¬ wiąże się najściślej, dając nam odpowiednik (¬A) Λ B zamiast ¬(A Λ B) . (Zapis dla zwykłej arytmetyki jest taki sam: -2 + 4 to 2, a nie -6.) W stosownych przypadkach używamy również nawiasów i nawiasów kwadratowych, aby wyjaśnić zamierzoną strukturę zdania i poprawić czytelność.

Przedstawiamy teraz logikę zdań. Opisujemy jego składnię (strukturę zdań) i semantykę (sposób określania prawdziwości zdań). Z nich wyprowadzamy prosty, syntaktyczny algorytm wnioskowania logicznego, który implementuje semantyczne pojęcie wynikania. Wszystko dzieje się oczywiście w świecie Wumpusa

Ta sekcja podsumowuje podstawowe koncepcje logicznej reprezentacji i rozumowania. Te piękne idee są niezależne od jakiejkolwiek szczególnej formy logiki. Dlatego odkładamy szczegóły techniczne tych form do następnej sekcji, używając zamiast tego znanego przykładu zwykłej arytmetyki. W sekcji 7.1 powiedzieliśmy, że bazy wiedzy składają się ze zdań. Zdania te są wyrażane zgodnie ze składnią języka reprezentacji, który określa wszystkie poprawnie sformułowane zdania. Pojęcie składni jest wystarczająco jasne w zwykłej arytmetyce: „x + t = 4” to zdanie dobrze uformowane, podczas gdy „x4y + =” nie. Logika musi również określać semantykę lub znaczenie zdań. Semantyka określa prawdziwość każdego zdania w odniesieniu do każdego możliwego świata. Na przykład semantyka arytmetyki określa, że ​​zdanie „x + y = 4 ” jest prawdziwe w świecie, w którym x wynosi 2, a y wynosi 2, ale fałszywe w świecie, w którym x wynosi 1, a y wynosi 1. W standardowej logice każde zdanie musi być prawdziwe lub fałszywe w każdym możliwym świecie – nie ma „pomiędzy”. Kiedy musimy być precyzyjni, zamiast „świata możliwego” używamy terminu model. Podczas gdy możliwe światy mogą być traktowane jako (potencjalnie) rzeczywiste środowiska, w których podmiot może się znajdować lub nie, modele są matematycznymi abstrakcjami, z których każda ma ustaloną wartość prawdy (prawda lub fałsz) dla każdego odpowiedniego zdania. Nieformalnie możemy myśleć o świecie możliwym jako na przykład, gdy mężczyźni i kobiety siedzą przy stole grając w brydża, a zdanie x + y = 4 jest prawdziwe, gdy w sumie są cztery osoby. Formalnie możliwe modele są po prostu wszystkimi możliwymi przypisaniami nieujemnych liczb całkowitych do zmiennych x i y. Każde takie przypisanie określa prawdziwość każdego zdania arytmetycznego, którego zmiennymi są x i y . Jeśli zdanie α jest prawdziwe w modelu m , mówimy , że m spełnia alfa lub czasami m jest modelem α . Używamy notacji M(α) do oznaczenia zbioru wszystkich modeli . Teraz, gdy mamy pojęcie prawdy, jesteśmy gotowi porozmawiać o logicznym rozumowaniu. Wiąże się to z relacją logicznego wynikania między zdaniami – ideą, że zdanie logicznie wynika z innego zdania. W notacji matematycznej piszemy

α |= β

oznaczać, że zdanie α pociąga za sobą zdanie β . Formalna definicja implikacji jest następująca: wtedy i tylko wtedy, gdy w każdym modelu, w którym α jest prawdziwa, β jest również prawdziwa. Używając właśnie wprowadzonej notacji, możemy zapisać

(Zwróć uwagę na kierunek tutaj ⊆: jeśli , to alfa jest silniejszym stwierdzeniem niż beta: wyklucza więcej możliwych światów.) Relacja wynikania jest znana z arytmetyki; cieszy nas pomysł, że zdanie x = 0 pociąga za sobą zdanie xy = 0 . Oczywiście w każdym modelu, w którym x wynosi zero, jest tak, że xy wynosi zero (niezależnie od wartości y ). Możemy zastosować ten sam rodzaj analizy do przykładu rozumowania wumpus-world podanego w poprzedniej sekcji. Rozważ sytuację na rysunku (b): agent wykrył nic w [1,1] i powiew w [2,1]. Te spostrzeżenia, w połączeniu z wiedzą agenta o regułach świata wumpusa, tworzą KB. Agenta interesuje, czy sąsiednie kwadraty [1,2], [2,2] i [3,1] zawierają doły. Każdy z trzech kwadratów może, ale nie musi, zawierać dołek, więc (pomijając na razie inne aspekty świata) mamy 2³ = 8 możliwych modeli. Te osiem modeli pokazano na rysunku

KB można traktować jako zbiór zdań lub jako pojedyncze zdanie, które potwierdza wszystkie poszczególne zdania. KB jest fałszywe w modelach, które są sprzeczne z tym, co wie agent – na przykład KB jest fałszywe w każdym modelu, w którym [1,2] zawiera dół, ponieważ nie ma wiatru w [1,1]. W rzeczywistości istnieją tylko trzy modele, w których KB jest prawdziwe, a na rysunku są one otoczone linią ciągłą. Rozważmy teraz dwa możliwe wnioski:

KB można traktować jako zbiór zdań lub jako pojedyncze zdanie, które potwierdza wszystkie poszczególne zdania. KB jest fałszywe w modelach, które są sprzeczne z tym, co wie agent — na przykład KB jest fałszywe w każdym modelu, w którym [1,2] zawiera dół, ponieważ nie ma wiatru w [1,1]. W rzeczywistości istnieją tylko trzy modele, w których KB jest prawdziwe i są one otoczone linią ciągłą na rysunku 7.5. Rozważmy teraz dwa możliwe wnioski:

Modele α₁ i α₂ otoczyliśmy liniami kropkowanymi odpowiednio na rysunkach (a) i (b). Po inspekcji widzimy, co następuje:

w każdym modelu, w którym KB jest prawdziwe, α1 też jest prawdziwe.

Stąd KB |= α₁: nie ma dołu w [1,2]. Możemy też to zobaczyć w niektórych modelach, w których KB jest prawdziwe, α₂ jest fałszywe.

Stąd KB nie pociąga za sobą α₂: agent nie może stwierdzić, że w [2,2] nie ma dołu. (Nie może też stwierdzić, że w [2,2] jest dół).

Powyższy przykład nie tylko ilustruje wynikanie, ale także pokazuje, w jaki sposób definicja wynikania może być zastosowana do wyprowadzania wniosków – to znaczy do wnioskowania logicznego. Algorytm wnioskowania przedstawiony na rysunku 7.5 nazywa się sprawdzaniem modelu, ponieważ wylicza wszystkie możliwe modele do sprawdzenia, czy jest prawdziwe we wszystkich modelach, w których KB jest prawdziwe, to znaczy, że M(KB) ⊆  M(α)

W zrozumieniu wnioskowania i wnioskowania pomocne może być myślenie o zbiorze wszystkich konsekwencji KB jako stogu siana i jako igle. Entailment jest jak igła w stogu siana; wnioskowanie jest jak znalezienie go. To rozróżnienie jest zawarte w pewnym formalnym zapisie: jeśli algorytm wnioskowania może pochodzić z KB , zapiszemy

co jest wymawiane jako „ α pochodzi od KB przez i ” lub „ i pochodzi od α od KB”. Algorytm wnioskowania, który wyprowadza tylko zaciągnięte zdania, nazywa się zachowaniem dźwięku lub prawdy. Zdrowość jest wysoce pożądaną właściwością. Niewłaściwa procedura wnioskowania zasadniczo wymyśla rzeczy w miarę postępu — zapowiada odkrycie nieistniejących igieł. Łatwo zauważyć, że sprawdzanie modelu, jeśli ma zastosowanie, jest rozsądną procedurą.

Pożądana jest również właściwość zupełności: algorytm wnioskowania jest kompletny, jeśli może wyprowadzić dowolne zdanie, które jest z nim związane. W przypadku prawdziwych stogów siana, których rozmiar jest skończony, wydaje się oczywiste, że systematyczne badanie zawsze może zdecydować, czy igła znajduje się w stogu siana. Jednak dla wielu baz wiedzy stóg konsekwencji jest nieskończony, a kompletność staje się ważną kwestią. Na szczęście istnieją kompletne procedury wnioskowania dla logik, które są wystarczająco ekspresyjne, aby obsłużyć wiele baz wiedzy. Opisaliśmy proces rozumowania, którego wnioski gwarantują prawdziwość w każdym świecie, w którym przesłanki są prawdziwe; w szczególności, jeśli KB jest prawdziwe w świecie rzeczywistym, to każde zdanie wyprowadzone z KB za pomocą procedury wnioskowania dźwiękowego jest również prawdziwe w świecie rzeczywistym. Tak więc, podczas gdy proces wnioskowania działa na „składni” – wewnętrznych konfiguracjach fizycznych, takich jak bity w rejestrach lub wzory elektrycznych impulsów w mózgu – proces ten odpowiada relacji w świecie rzeczywistym, w której pewien aspekt świata rzeczywistego ma miejsce z racji inne aspekty realnego świata. Tę zależność między światem a reprezentacją ilustruje rysunek

Ostatnią kwestią do rozważenia jest uziemienie – związek między logicznymi procesami rozumowania a rzeczywistym środowiskiem, w którym istnieje agent. W szczególności, skąd wiemy, że KB jest prawdziwe w prawdziwym świecie? (W końcu KB to po prostu „składnia” w głowie agenta.) Jest to pytanie filozoficzne, o którym napisano wiele, wiele książek. Prostą odpowiedzią jest to, że czujniki agenta tworzą połączenie. Na przykład nasz agent ze świata wumpusa ma czujnik zapachu. Program agenta tworzy odpowiednie zdanie za każdym razem, gdy pojawia się zapach. Wtedy, ilekroć to zdanie znajduje się w bazie wiedzy, jest prawdziwe w prawdziwym świecie. Tak więc znaczenie i prawdziwość zdań percepcyjnych są definiowane przez procesy odczuwania i konstruowania zdań, które je wytwarzają. A co z resztą wiedzy agenta, na przykład z przekonaniem, że wumpusy powodują zapachy na sąsiednich placach? Nie jest to bezpośrednia reprezentacja pojedynczego spostrzeżenia, ale ogólna zasada – wywodząca się być może z doświadczenia percepcyjnego, ale nie tożsama ze stwierdzeniem tego doświadczenia. Takie ogólne zasady są tworzone przez proces konstruowania zdań zwany uczeniem. Uczenie się jest omylne. Może się zdarzyć, że wumpusy powodują nieprzyjemne zapachy, z wyjątkiem 29 lutego w latach przestępnych, kiedy to biorą kąpiel. Dlatego KB , może nie być prawdziwe w prawdziwym świecie, ale przy dobrych procedurach uczenia się jest powód do optymizmu.

W tej części opisujemy środowisko, w którym agenci bazujący na wiedzy mogą pokazać swoją wartość. każdego, kto wejdzie do tych pomieszczeń (z wyjątkiem wumpusa, który jest zbyt duży, aby wpaść do niego). Jedyną zbawienną cechą tego ponurego środowiska jest możliwość znalezienia kupy złota. Świat Wumpusa to jaskinia składająca się z pomieszczeń połączonych przejściami. Gdzieś w jaskini czai się straszliwy wumpus, bestia, która pożera każdego, kto wejdzie do jej pokoju. Wumpus może zostać zastrzelony przez agenta, ale agent ma tylko jedną strzałę. Niektóre pokoje zawierają doły bez dna, które uwięzią Chociaż świat wumpusów jest raczej oswojony według współczesnych standardów gier komputerowych, ilustruje kilka ważnych punktów dotyczących inteligencji. Przykładowy świat wumpusa pokazano na rysunku

Dokładną definicję środowiska zadaniowego podaje opis PEAS:

WYNIKI: +1000 za wyjście z jaskini ze złotem, -1000 za wpadnięcie do dołu lub zjedzenie przez wumpusa, -1 za każdą wykonaną akcję i -10 za użycie strzały. Gra kończy się, gdy agent zginie lub gdy agent wydostanie się z jaskini.

ŚRODOWISKO: Siatka 4×4 pomieszczeń ze ścianami otaczającymi siatkę. Agent zawsze zaczyna na kwadracie oznaczonym [1,1] skierowanym na wschód. Lokalizacje złota i wumpusa są wybierane losowo, z równomiernym rozkładem, z pól innych niż pole startowe. Ponadto każde pole inne niż start może być dołem, z prawdopodobieństwem 0,2.

AKTUATORY: Agent może poruszyć się do przodu, skręcić w lewo o 90o lub skręcić w prawo o 90o . Agent umrze żałosną śmiercią, jeśli wejdzie na plac zawierający dół lub żywego wumpusa. (Bezpieczne, choć śmierdzące, jest wejście na plac z martwym wumpusem.) Jeśli agent próbuje iść do przodu i wpada na ścianę, agent się nie rusza. Akcja Chwyć może zostać użyta do podniesienia złota, jeśli znajduje się ono na tym samym polu, co agent. Akcja Shoot może być wykorzystana do wystrzelenia strzały w linii prostej w kierunku, w który zwrócony jest agent. Strzała kontynuuje, dopóki nie uderzy (a tym samym zabije) wumpusa lub uderzy w ścianę. Agent ma tylko jedną strzałę, więc tylko pierwsza akcja Strzału ma jakikolwiek efekt. Na koniec akcję Wspinacz można wykorzystać do wyjścia z jaskini, ale tylko z placu [1,1].

CZUJNIKI: Agent posiada pięć czujników, z których każdy podaje jeden bit informacji:

‐ W kwadratach bezpośrednio (nie po przekątnej) przylegających do wumpusa, agent wyczuje Smród.

‐ Na polach bezpośrednio przylegających do dołu agent dostrzeże bryzę.

‐ W kwadracie, gdzie znajduje się złoto, agent dostrzeże Brokat.

‐ Kiedy agent wejdzie na ścianę, dostrzeże Uderzenie.

‐ Kiedy wumpus zostaje zabity, emituje żałosny krzyk, który można wyczuć w dowolnym miejscu jaskini.

Percepty zostaną przekazane programowi agenta w postaci listy pięciu symboli; na przykład, jeśli jest smród i bryza, ale nie ma blasku, uderzenia lub krzyku, program agenta otrzyma [Stench,Breeze,None,None,None].

Możemy scharakteryzować środowisko wumpusa w różnych wymiarach podanych w rozdziale 2 . Oczywiście jest deterministyczny, dyskretny, statyczny i działa na zasadzie jednego agenta. (Na szczęście wumpus się nie porusza.) Jest to sekwencyjne, ponieważ nagrody mogą pojawić się dopiero po wykonaniu wielu działań. Jest to częściowo widoczne, ponieważ niektóre aspekty stanu nie są bezpośrednio dostrzegalne: lokalizacja agenta, stan zdrowia wumpusa i dostępność strzały. Co do lokalizacji zagłębień i wumpusa: moglibyśmy traktować je jako nieobserwowane części stanu – w takim przypadku model przejściowy dla środowiska jest całkowicie znany, a znalezienie lokalizacji zagłębień uzupełnia wiedzę agenta o stanie. Alternatywnie, moglibyśmy powiedzieć, że sam model przejścia jest nieznany, ponieważ agent nie wie, które działania Forward są fatalne – w takim przypadku odkrycie lokalizacji dołów i wumpusów uzupełnia wiedzę agenta o modelu przejścia. Dla agenta w środowisku głównym wyzwaniem jest jego początkowa nieznajomość konfiguracji środowiska; przezwyciężenie tej ignorancji wydaje się wymagać logicznego rozumowania. W większości przypadków w świecie Wumpus agent może bezpiecznie odzyskać złoto. Czasami agent musi wybrać między powrotem do domu z pustymi rękami a narażeniem się na śmierć, aby znaleźć złoto. Około 21% środowisk jest całkowicie niesprawiedliwych, ponieważ złoto znajduje się w dole lub jest otoczone dołami. Przyjrzyjmy się opartemu na wiedzy agentowi wumpus eksplorującemu środowisko pokazane na rysunku. Używamy nieformalnego języka reprezentacji wiedzy składającego się z zapisywania symboli w siatce

Początkowa baza wiedzy agenta zawiera opisane wcześniej reguły środowiska; w szczególności wie, że jest w [1,1] i że [1,1] jest bezpiecznym kwadratem; oznaczamy to odpowiednio przez „A” i „OK” w kwadracie [1,1]. Pierwsza percepta to [Brak,Brak,Brak,Brak,Brak], z której agent moe wywnioskować, e sąsiednie kwadraty [1,2] i [2,1] są wolne od niebezpieczeństw – są w porządku. Rysunek 7.3(a) pokazuje stan wiedzy agenta w tym momencie. Ostrożny agent wejdzie tylko na pole, o którym wie, że jest w porządku. Załóżmy, że agent zdecyduje się przejść do [2,1]. Agent dostrzega bryzę (oznaczoną literą „B”) w [2,1], więc na sąsiednim kwadracie musi być dziura. Zagłębienie nie może być w [1,1], zgodnie z zasadami gry, więc musi być zagłębienie w [2,2] lub [3,1] lub w obu. Notacja „P?” na Rysunku 7.3(b) wskazuje możliwy dół w tych kwadratach. W tym momencie jest tylko jeden znany plac, który jest w porządku i który nie został jeszcze odwiedzony. Więc rozważny agent odwróci się, wróć do [1,1], a następnie przejdź do [1,2]. Agent wyczuwa smród w [1,2], co skutkuje stanem wiedzy przedstawionym na rysunku (a). Smród w [1,2] oznacza, że ​​w pobliżu musi być wumpus. Ale wumpus nie może być w [1,1], zgodnie z regułami gry, i nie może być w [2,2] (albo agent wykryłby smród, gdy był w [2,1]). Dlatego agent może wywnioskować, że wumpus znajduje się w [1,3]. Notacja W! wskazuje ten wniosek. Co więcej, brak bryzy w [1,2] oznacza, że ​​w [2,2] nie ma dołu. Jednak agent już wywnioskował, że w [2,2] lub [3,1] musi być dół, co oznacza, że ​​musi być w [3,1]. Jest to dość trudne wnioskowanie, ponieważ łączy wiedzę zdobytą w różnym czasie w różnych miejscach i polega na braku percepcji, aby zrobić jeden kluczowy krok. Agent udowodnił sobie, że w [2,2] nie ma ani dołu, ani wumpusa, więc można się tam przenieść. Nie pokazujemy stanu wiedzy agenta w [2,2]; po prostu zakładamy, że agent obraca się i przesuwa do [2,3], co daje nam rysunek (b) . W [2,3] agent wykrywa brokat, więc powinien złapać złoto i wrócić do domu. Należy zauważyć, że w każdym przypadku, w którym agent wyciąga wniosek z dostępnych informacji, wniosek ten jest gwarantowany, jeśli dostępne informacje są prawidłowe. Jest to podstawowa właściwość logicznego rozumowania. W pozostałej części opisujemy, jak budować agentów logicznych, którzy mogą reprezentować informacje i wyciągać wnioski, takie jak te opisane w poprzednich akapitach.