Wcześniej mówiliśmy, że modele języka logicznego są strukturami formalnymi, które konstytuują rozważane światy możliwe. Każdy model łączy słownik zdań logicznych z elementami świata możliwego, dzięki czemu można ustalić prawdziwość dowolnego zdania. W ten sposób modele logiki zdań łączą symbole zdań z predefiniowanymi wartościami prawdy. Modele logiki pierwszego rzędu są znacznie ciekawsze. Po pierwsze, mają w sobie przedmioty! Dziedziną modelu jest zbiór obiektów lub elementów domeny, które zawiera. Domena musi być niepusta – każdy możliwy świat musi zawierać przynajmniej jeden obiekt. Matematycznie rzecz biorąc, nie ma znaczenia, jakie są te obiekty – liczy się tylko to, ile jest ich w każdym konkretnym modelu – ale dla celów pedagogicznych użyjemy konkretnego przykładu. Rysunek przedstawia model z pięcioma obiektami: Ryszard Lwie Serce, król Anglii od 1189 do 1199; jego młodszy brat, zły król Jan, który rządził od 1199 do 1215 roku; lewe nogi Richarda i Johna; i koronę.
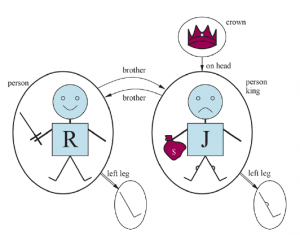
Obiekty w modelu mogą być powiązane na różne sposoby. Na rysunku Richard i John są braćmi. Formalnie rzecz biorąc, relacja to po prostu zbiór krotek obiektów, które są ze sobą powiązane. (Krótka jest zbiorem obiektów ułożonych w ustalonym porządku i jest zapisana w nawiasach ostrych otaczających obiekty.) Zatem relacja braterstwa w tym modelu jest zbiorem
{⟨Richard the Lionheart, King John⟩, ⟨King John, Richard the Lionheart⟩}
(Tu nazwaliśmy obiekty w języku angielskim, ale jeśli chcesz, możesz w myślach zastąpić je obrazkami.) Korona znajduje się na głowie króla Jana, więc relacja „na głowie” zawiera tylko jedną krotkę, 〈korona , króla Jana. Relacje „brat” i „na głowie” są relacjami binarnymi – to znaczy łączą pary obiektów. Model zawiera również jednoargumentowe relacje lub właściwości: właściwość „osoby” jest prawdziwa zarówno w przypadku Richarda, jak i Johna; własność „króla” dotyczy tylko Jana (przypuszczalnie dlatego, że Ryszard nie żyje w tym momencie); a właściwość „korony” dotyczy tylko korony. Pewne rodzaje relacji najlepiej traktować jako funkcje, ponieważ dany obiekt musi być w ten sposób powiązany z dokładnie jednym obiektem. Na przykład każda osoba ma jedną lewą nogę, więc model ma jednoargumentową funkcję „lewa noga” – mapowanie z jednoelementowej krotki na obiekt – która obejmuje następujące mapowania:
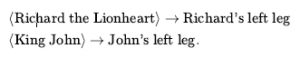
Ściśle mówiąc, modele w logice pierwszego rzędu wymagają funkcji całkowitych, to znaczy, że każda krotka wejściowa musi mieć wartość. Zatem korona musi mieć lewą nogę, podobnie jak każda z lewych nóg. Istnieje techniczne rozwiązanie tego niezręcznego problemu, polegające na dodatkowym „niewidzialnym” obiekcie, jakim jest lewa noga wszystkiego, co nie ma lewej nogi, łącznie z nim samym. Na szczęście tak długo, jak nie czyni się twierdzeń o lewych nogach rzeczy, które nie mają lewych nóg, te szczegóły techniczne nie mają znaczenia. Do tej pory opisaliśmy elementy, które wypełniają modele dla logiki pierwszego rzędu. Inną istotną częścią modelu jest powiązanie tych elementów ze słownictwem zdań logicznych, które wyjaśnimy dalej.