Jak stwierdzono na początku rozdziału, agent logiczny działa poprzez wydedukowanie, co należy zrobić z bazy wiedzy zdań o świecie. Baza wiedzy składa się z aksjomatów – ogólnej wiedzy o tym, jak działa świat – i zdań percepcyjnych uzyskanych z doświadczenia agenta w określonym świecie. W tej części skupimy się na problemie wydedukowania obecnego stanu świata wumpusów – gdzie jestem, czy ten kwadrat jest bezpieczny i tak dalej. Agent wie, że na polu startowym nie ma dołu (¬P1,1) ani wumpusa (¬W1,1 ). Co więcej, dla każdego kwadratu wie, że jest przewiewny wtedy i tylko wtedy, gdy sąsiedni kwadrat ma dół; a kwadrat jest śmierdzący wtedy i tylko wtedy, gdy sąsiedni kwadrat ma wumpusa. W związku z tym zawieramy duży zbiór zdań o następującej postaci:
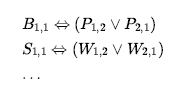
Agent wie też, że jest dokładnie jeden wumpus. Wyraża się to w dwóch częściach. Po pierwsze, musimy powiedzieć, że istnieje co najmniej jeden wumpus:
![]()
Następnie musimy powiedzieć, że jest co najwyżej jeden wumpus. Dla każdej pary lokacji dodajemy zdanie mówiące, że przynajmniej jedna z nich musi być wolna od wumpusa:
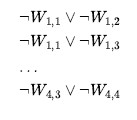
Jak na razie dobrze. Rozważmy teraz spostrzeżenia agenta. Używamy tego S1,1 , aby powiedzieć, że w [1,1] jest smród; czy możemy użyć jednej propozycji, Stnech aby oznaczać, że agent wyczuwa smród? Niestety nie możemy: gdyby nie było smrodu w poprzednim kroku czasowym, to byłoby ¬Stench już stwierdzone, a nowe stwierdzenie spowodowałoby po prostu sprzeczność. Problem zostaje rozwiązany, gdy zdamy sobie sprawę, że percepcja stwierdza coś tylko o aktualnym czasie. Tak więc, jeśli krok czasowy wynosi 4, wtedy dodajemy Stench do bazy wiedzy, a nie Strench – starannie unikając wszelkich sprzeczności z . To samo dotyczy percepcji wiatru, uderzenia, blasku i krzyku. Pomysł kojarzenia zdań z krokami czasowymi rozciąga się na każdy aspekt świata, który zmienia się w czasie. Na przykład początkowa baza wiedzy obejmuje L01,1 – agent jest w kwadracie [1,1] w czasie 0 – oraz Facingeast0, HaveArrow0 , i WumpusAlive0 . Używamy rzeczownika fluent (z łac. fluens), aby odnieść się do zmieniającego się aspektu świata. „Płynna” jest synonimem „zmiennej stanu” w znaczeniu opisanym w omówieniu reprezentacji podzielonych na czynniki w Sekcji 2.4.7 na stronie 58. Symbole związane ze stałymi aspektami świata nie wymagają indeksu górnego czasu i są czasami nazywane atemporalnymi. zmienne. Możemy połączyć postrzeganie smrodu i wiatru bezpośrednio z właściwościami kwadratów, w których są one doświadczane w następujący sposób. Dla dowolnego kroku czasowego i dowolnego kwadratu [x,y] zapewniamy:
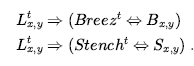
Teraz oczywiście potrzebujemy aksjomatów, które pozwolą agentowi śledzić biegle, takie jak Ltx,y . Te biegłości zmieniają się w wyniku działań podejmowanych przez agenta, więc w terminologii rozdziału 3 musimy zapisać model przejściowy świata wumpus jako zbiór zdań logicznych. Najpierw potrzebujemy symboli propozycji dla wystąpień akcji. Podobnie jak w przypadku perceptów, te symbole są indeksowane według czasu; zatem Forward0 oznacza to, że agent wykonuje akcję Forward w czasie 0. Zgodnie z konwencją, percept dla danego kroku czasowego ma miejsce jako pierwszy, po nim następuje akcja dla tego kroku czasowego, a następnie następuje przejście do następnego kroku czasowego. Aby opisać, jak zmienia się świat, możemy spróbować napisać aksjomaty efektów, które określają wynik działania w następnym kroku czasowym. Na przykład, jeśli agent znajduje się w lokalizacji [1,1] zwrócony na wschód w czasie 0 i porusza się do przodu, wynikiem jest to, że agent znajduje się w kwadracie [2,1] i nie znajduje się już w t :
![]()
Potrzebowalibyśmy jednego takiego zdania dla każdego możliwego kroku czasowego, dla każdego z 16 kwadratów i każdej z czterech orientacji. Potrzebowalibyśmy również podobnych zdań dla innych akcji: Chwyć, Strzelaj, Wspinaj się, Skręć w lewo i Skręć w prawo. Załóżmy, że agent decyduje się ruszyć Naprzód w czasie 0 i potwierdza ten fakt w swojej bazie wiedzy. Mając aksjomat efektu w połączeniu z początkowymi twierdzeniami o stanie w czasie 0, agent może teraz wywnioskować, że jest w [2,1]. To jest, ASK(KB,L1,2,1) = true . Jak na razie dobrze. Niestety, jeśli my ASK(KB,HaveArrow1), odpowiedź jest fałszywa, to znaczy agent nie może udowodnić, że nadal ma strzałę; ani nie może udowodnić, że jej nie ma! Informacja została utracona, ponieważ aksjomat efektu nie określa tego, co pozostaje niezmienione w wyniku działania. Konieczność zrobienia tego powoduje powstanie problemu z ramą. Jednym z możliwych rozwiązań problemu ramy byłoby dodanie aksjomatów ramy, wyraźnie potwierdzających wszystkie zdania, które pozostają takie same.Na przykład za każdym razem mielibyśmy miejsce, w którym wyraźnie wymienimy każde zdanie, które pozostaje niezmienione od czasu t do czasu t+1 w ramach akcji Naprzód. Chociaż agent teraz wie, że nadal ma strzałę po przejściu do przodu i że wumpus nie umarł ani nie wrócił do życia, mnożenie aksjomatów ramowych wydaje się wyjątkowo nieefektywne. W świecie o m różnych działaniach i n biegach, zbiór aksjomatów ramy będzie miał rozmiar O(m,n). Ta konkretna manifestacja problemu ramek jest czasami nazywana problemem ram reprezentacyjnych. Problem odegrał znaczącą rolę w historii sztucznej inteligencji; omówimy to dalej w uwagach na końcu.
Problem ram reprezentacyjnych jest o tyle istotny, że świat rzeczywisty ma bardzo wiele biegłości, delikatnie mówiąc. Na szczęście dla nas, ludzi, każde działanie zwykle zmienia nie więcej niż niewielka liczba k tych płynnych ruchów – świat wykazuje lokalność. Rozwiązanie problemu ramy reprezentacyjnej wymaga zdefiniowania modelu przejścia za pomocą zestawu aksjomatów rozmiaru O(m,k) , a nie rozmiaru O(m,n). Istnieje również problem z ramą inferencyjną: problem przewidywania w czasie wyników t-krokowego planu działania w czasie O(kt), a nie O(n,t)
Rozwiązanie problemu polega na zmianie skupienia z pisania aksjomatów o działaniach na pisanie aksjomatów o biegłościach. Tak więc dla każdego płynnego F , będziemy mieli aksjomat, który definiuje wartość logiczną prawda Ft+1 w kategoriach płynnych (w tym samo F) w czasie t i działań, które mogły mieć miejsce w czasie t . Teraz wartość prawdziwości Ft+1 można ustawić na jeden z dwóch sposobów: albo działanie w czasie t powoduje, że F jest prawdziwe w t+1 , albo F było już prawdziwe w czasie t i działanie w czasie t nie powoduje, że jest fałszywe. Aksjomat o tej postaci nazywa się aksjomatem następcy stanu i ma postać:
![]()
Jednym z najprostszych aksjomatów stanu następcy jest ten dla HaveArrow. Ponieważ nie ma akcji przeładowania, część ActionCausesFt znika i zostajemy z
![]()
W przypadku lokalizacji agenta aksjomaty stanów następczych są bardziej rozbudowane. Na przykład, Lt+11,1jest prawdą, jeśli: (a) agent przesunął się do przodu z [1,2], gdy jest skierowany na południe, lub z [2,1], gdy jest skierowany na zachód; lub (b) Lt1,1 było już prawdziwe, a akcja nie spowodowała ruchu (albo dlatego, że akcja nie była Naprzód, albo uderzyła w ścianę). Napisane w logice zdań, staje się to

Mając kompletny zestaw aksjomatów stanów następców i innych aksjomatów wymienionych na początku tej sekcji, agent będzie w stanie ZAPYTAĆ i odpowiedzieć na wszelkie pytania dotyczące aktualnego stanu świata. Na przykład początkowa sekwencja percepcji i działań to:

W tym momencie mamy ASK(KB, L61,2) = true więc agent wie, gdzie to jest. Ponadto, ASK(KB, W1,3) = true i ASK(KB, P 3,1,) = true, więc agent znalazł wumpusa i jeden z dołów. Najważniejszym pytaniem dla agenta jest to, czy kwadrat jest w porządku, aby przenieś się do – to znaczy, czy kwadrat jest wolny od dołu lub żywego wumpusa. Wygodnie jest dodać do tego aksjomaty, które mają postać
![]()
Na koniec ASK(KB, OK62,2) = true , więc przejście do kwadratu [2,2] jest OK. W rzeczywistości, mając do dyspozycji solidny i kompletny algorytm wnioskowania, taki jak DPLL, agent może odpowiedzieć na każde pytanie, na które można odpowiedzieć, które kwadraty są w porządku – i może to zrobić w ciągu zaledwie kilku milisekund dla małych i średnich światów wumpus. Rozwiązanie problemów z ramami reprezentacyjnymi i inferencyjnymi jest dużym krokiem naprzód, ale zgubny problem pozostaje: musimy potwierdzić, że wszystkie niezbędne warunki wstępne działania są spełnione, aby miało ono zamierzony skutek. Powiedzieliśmy, że akcja Naprzód przesuwa agenta do przodu, chyba że na drodze stoi ściana, ale istnieje wiele innych niezwykłych wyjątków, które mogą spowodować niepowodzenie akcji: agent może się potknąć i upaść, doznać ataku serca, zostać niesionym przez gigantyczne nietoperze itp. Określanie wszystkich tych wyjątków nazywa się problemem kwalifikacji. W logice nie ma kompletnego rozwiązania; projektanci systemów muszą kierować się rozsądkiem przy podejmowaniu decyzji o tym, jak szczegółowe chcą być w określaniu swojego modelu, a jakie szczegóły chcą pominąć. W rozdziale 12 zobaczymy, że teoria prawdopodobieństwa pozwala nam podsumować wszystkie wyjątki bez wyraźnego ich nazywania.