Niektóre problemy z SAT są trudniejsze niż inne. Proste problemy można rozwiązać dowolnym starym algorytmem, ale ponieważ wiemy, że SAT jest NP-zupełny, przynajmniej niektóre instancje problemów muszą wymagać wykładniczego czasu wykonywania. W rozdziale 6 zobaczyliśmy zaskakujące odkrycia dotyczące pewnych rodzajów problemów. Na przykład problem n-królowych – uważany za dość skomplikowany dla algorytmów wyszukiwania z nawrotem – okazał się banalnie łatwy dla lokalnych metod wyszukiwania, takich jak min-konflikty. Dzieje się tak, ponieważ rozwiązania są bardzo gęsto rozmieszczone w przestrzeni przydziałów, a każde początkowe przypisanie gwarantuje, że znajdzie rozwiązanie w pobliżu. Tak więc n-królowe jest łatwe, ponieważ nie jest ograniczone. Kiedy przyjrzymy się problemom spełnialności w spójnej postaci normalnej, problem niedostatecznie ograniczony to taki, w którym stosunkowo niewiele klauzul ogranicza zmienne. Na przykład, oto losowo wygenerowane zdanie 3-CNF z pięcioma symbolami i pięcioma klauzulami:
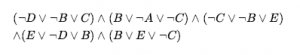
Szesnaście z 32 możliwych przypisań to modele tego zdania, więc średnio potrzeba tylko dwóch losowych zgadnięć, aby znaleźć model. Jest to łatwy problem spełnialności, podobnie jak większość takich problemów z niepełnym ograniczeniem. Z drugiej strony problem nadmiernie ograniczony ma wiele klauzul odnoszących się do liczby zmiennych i prawdopodobnie nie będzie miał rozwiązań. Nadmiernie ograniczone problemy są często łatwe do rozwiązania, ponieważ ograniczenia szybko prowadzą albo do rozwiązania, albo do ślepego zaułka, z którego nie ma ucieczki. Aby wyjść poza te podstawowe intuicje, musimy dokładnie określić, w jaki sposób generowane są losowe zdania. Notacja CNFk(m,n)oznacza zdanie k-CNF z m klauzulami i n symbolami, gdzie klauzule są wybierane jednolicie, niezależnie i bez zamiany spośród wszystkich klauzul z k różnymi literałami, które są losowo dodatnie lub ujemne. (Symbol nie może pojawić się dwa razy w zdaniu, ani zdanie nie może pojawić się dwa razy w zdaniu). Mając źródło losowych zdań, możemy zmierzyć prawdopodobieństwo spełniania. Rysunek (a) przedstawia prawdopodobieństwo wystąpienia CNF3(m,50) , czyli zdań z 50 zmiennymi i 3 literałami na zdanie, jako funkcję stosunku zdanie/symbol, . Jak się spodziewamy, dla małych m/n prawdopodobieństwo spełniania jest bliskie 1, a dla dużych m/n jest bliskie 0. Prawdopodobieństwo dość gwałtownie spada wokół m/n = 4.3 . Empirycznie stwierdzamy, że „klif” pozostaje mniej więcej w tym samym miejscu (dla k = 3 ) i staje się coraz ostrzejszy wraz ze wzrostem n.
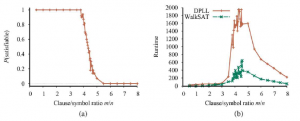
Teoretycznie hipoteza progu spełnialności mówi, że dla każdego k ≥ 3 , istnieje stosunek progowy rk taki, że jeśli n dąży do nieskończoności prawdopodobieństwo że CNFk(rn,n) jest spełnialne wynosi 1 dla wszystkich wartości poniżej progu i 0 dla wszystkich wartości powyżej. Przypuszczenie pozostaje niesprawdzone, nawet w szczególnych przypadkach, takich jak k = 3 . Niezależnie od tego, czy jest to twierdzenie, czy nie, ten rodzaj progowania jest z pewnością powszechny, w przypadku problemów spełnialności, jak również innych rodzajów problemów NP-trudnych. Teraz, gdy mamy już dobry pomysł, gdzie znajdują się problemy dające się zaspokoić, a gdzie nie, następne pytanie brzmi: gdzie są problemy trudne? Okazuje się, że często są one również na progu. Rysunek (b) pokazuje, że 50-symbolowe problemy przy wartości progowej 4,3 są około 20 razy trudniejsze do rozwiązania niż te o stosunku 3,3. Problemy o ograniczonych ograniczeniach są najłatwiejsze do rozwiązania (ponieważ tak łatwo jest odgadnąć rozwiązanie); problemy z nadmiernymi ograniczeniami nie są tak łatwe, jak problemy z niedoborem ograniczeń, ale nadal są znacznie łatwiejsze niż te tuż przy progu.